递推
算法笔记第二期
递推
概念
- 所谓递推,指的是从已知的初始条件出发,依据某种特定的关系,逐次推导出所要求的各种中间结果,直至得到结果的算法。
- 从已知条件出发逐步推到问题结果,此种方法叫顺推。从问题出发逐步推到已知条件,此种方法叫逆推。不管怎么推导,关键在于找到递推式。充分发挥计算机擅长重复处理的特点。
- 递推方法是一种重要的数学方法,将一个复杂问题分解为连续若干的简单运算。
递推式
- 把序列a0、a1、...、an,...,简单记为{an}。一个把an与某些ai(i < n)联系起来的等式叫做关于序列{an}的递推方程
- 假定有了初值,和递推式,就可以确定这个唯一序列
举例说明
阶乘问题
n的阶乘等于1×2×3...×n。其中n为正整数,假定f(n)表示n的阶乘。根据阶乘的计算方法可以得出
f(n) = 1 × 2 × 3 ... × n
f(n) = (1 × 2 × 3 ... × (n-1)) × n = f(n-1) × n
而初值 f(1) = 1. 根据初值和上面的递推式可以得出这个序列中的每一个值。
问题分析
例1、兔子繁殖问题
这是一个有趣的古典数学问题:有一对兔子,从出生后一个月就可以长大成熟,再过一个月就可以生育一对小兔子,并且之后每个月都能生育一对小兔子。
假设有一对刚出生的小兔子,问10个月后的兔子总数为多少?(假设所有兔子都不死)
分析
我们可以将每个月份开始时,兔子的情况列出如下表格
| 月份 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| 幼兔 | 1 | 0 | 1 | 1 | 2 | 3 |
| 成兔 | 0 | 1 | 1 | 2 | 3 | 5 |
| 总数 | 1 | 1 | 2 | 3 | 5 | 8 |
根据分析表格很容易看出幼兔经过一个月后成为成兔,成兔的数量为上一个月成兔加上幼兔的数量(即上月总数),而幼兔的数量为上一个月成兔的数量。
T(n)表示第n个月幼兔的数,S(n)表示第n个月成兔的数量,f(n)表示第n个月总数
S(n) = T(n-1) + S(n-1) = f(n - 1)
T(n) = S(n-1) = T(n-2) + S(n-2) = f(n-2)
f(n) = T(n) + S(n) = f(n-1) + f(n-2)
也可以简单从如下角度考虑,第n个月的兔子数量,由两部分构成
1、上月存在的兔子数量f(n-1)
2、本月新出生的兔子f(n-2)
很明显,递推式已经得出,初值f(1) = 1,f(2) = 2
程序实现
/**
顺推法
根据初值和递推公式得到最终结果
**/
#include <cstdio>
long long a[50]; //斐波那契数列增长过快,因此使用long long数据类型
int main () {
int n;
a[1] = 2, a[2] = 2;
scanf ("%d", &n);
for (int i = 3; i <= n; i++)
a[i] = a[i-1] + a[i-2];
printf("%lld\n", a[n]);
return 0;
}
/**
逆推法:
一般是递归实现,从最终结果出发,不断缩小直至递归边界。
方法效率过低。
**/
#include <cstdio>
long long fib (int n) {
if (n == 1 || n == 2)
return 1;
return fib(n-1) + fib(n-2);
}
int main () {
int n;
scanf ("%d", &n);
printf("%lld\n", fib(5));
return 0;
}
记忆化操作
- 使用递归求解问题的时候,通常效率低下,原因在重复计算
拿斐波那契数列举例,计算f(6)的过程如下图所示
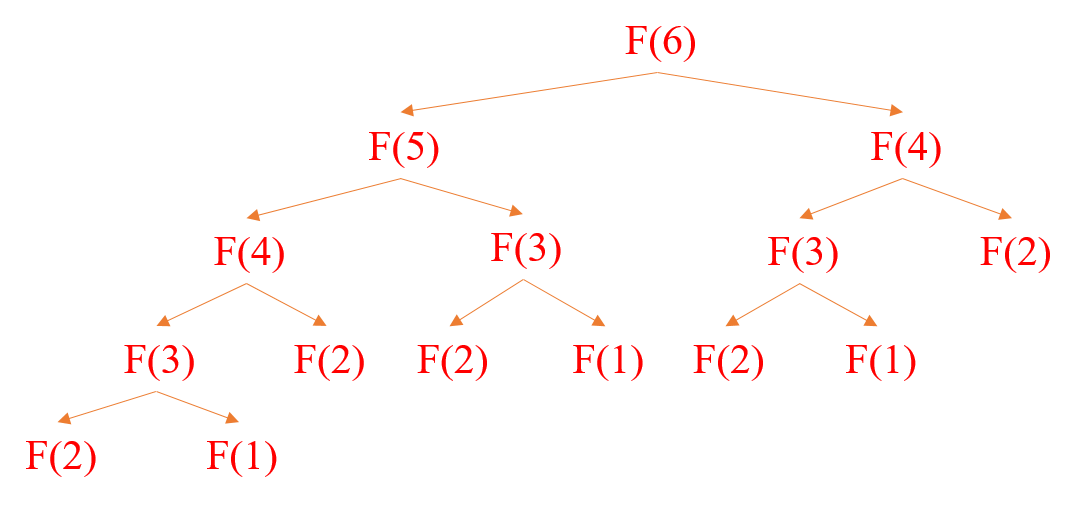
明显发现除了边界,其他的中间值例如f(4)、f(3)等被重复计算多次,在我们计算f(5)的过程中实际上,f(4)、f(3)也被算了出来,在这种情况下,右边的f(4)依然在重复进行计算。要是能在在计算过程中,记住被计算过的中间值,这样操作就会大大增加效率。
程序如下
#include <cstdio>
#define N 100
long long bin[N]; //记忆化数组,初始化为0表示全部没有被计算过
long long fib (int n) {
if (n == 1 || n == 2)
return 1;
if (!bin[n])
bin[n] = fib(n-1) + fib(n-2); //每次计算都存储
return bin[n];
}
int main () {
int n;
scanf ("%d", &n);
printf("%lld\n", fib(n));
return 0;
}
记忆化的操作通过空间换取了时间效率。将递归的中间值存放在数组中,当需要某个状态的值时,只需检查下数组中相应位置是否有值,如果有直接调用,如果没有再行计算。
小结
递推问题的关键点:
- 问题可以按照事物的发展分成多个阶段状态
- 除初始状态,每一个阶段都与前面的阶段有联系,可以根据递推关系式求得
- 实现通常是顺序推算,或者记忆化。
训练
上台阶问题
【问题描述】
楼梯有n(71>n>0)阶台阶,上楼时可以一步上1阶,也可以一步上2阶,也可以一步上3阶,编程计算共有多少种不同的走法。
【输入】
输入的每一行包括一组测试数据,即为台阶数n。最后一行为0,表示测试结束。
【输出】
每一行输出对应一行输入的结果,即为走法的数目。
【输入样例】
1
2
3
4
0
【输出样例】
1
2
4
7
分析可得递推式f(n) = f(n-1) + f(n-2)+f(n-3)
原因在于,我们只考虑走最后一步的情况,最后一步实际上有三种走法,一种是走一步,一种是走两步,一种是走三步。走一步的总步数为f(n-1),走两步的总步数为f(n-2),走三步的总步数为f(n-3)。因此f(n) = f(n-1) + f(n-2) + f(n-3)。
代码
#include <cstdio>
long long f[80];
int main () {
int n;
f[1] = 1;
f[2] = 2;
f[3] = 4;
while (1) {
scanf ("%d", &n);
if (n == 0) return 0;
if (!f[n])
for (int i = 4; i <= n; i++)
f[i] = f[i-1] + f[i-2] + f[i-3];
printf("%d\n", f[n]);
}
return 0;
}
将走楼梯的过程进行分解,走完n个楼梯通过若干动作来完成。如果只考虑最后一步走了多少楼梯,就可以实现一个降维操作。
二叉树个数
【问题描述】
二叉树是每个节点最多有两个子树的树形结构,且有左右子树之分,次序不能颠倒。给出二叉树的节点数n,请问有多少种不同的形态。
【输入】
一行N。(1<=n<=15)
【输出】
节点为n的二叉树共有多少种不同的形态
【样例输入】
3
【样例输出】
5
题目说明:
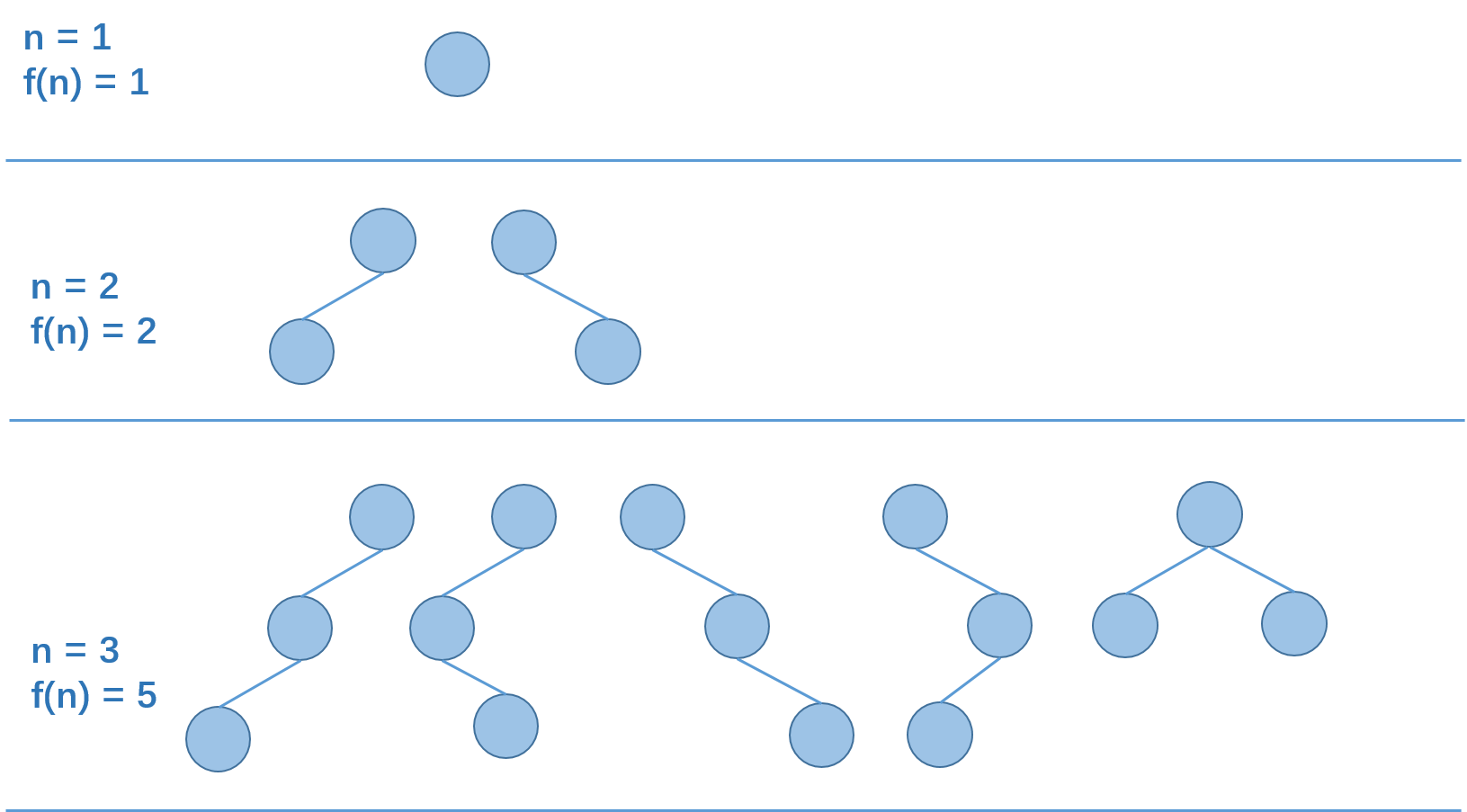
题目分析
不难发现,二叉树的左右子树其本质上也是一棵二叉树。并且左右子树的节点左右位置不同也会导致整棵树的形态不同。
假定f(n)表示n个节点的二叉树总共的形态数
现在来构造一棵二叉树,首先取出一个节点作为根节点,接下来构造左右子树,左边可以放0个节点,对应右边放n-1个节点,那么这种情况的总形态数就是f(0)×f(n-1),如果左边放1个节点右边放n-2个节点那么总形态数为f(1)×f(n-2)。因此总的形态数为f(n) = f(0) × f(n-1) + f(1) × f(n-2) + ... + f(n-1) × f(0)
而初值f(0) = 1, f(1) = 1。
参考程序
/**
顺推
**/
#include <cstdio>
long long f[16];
int main () {
int n;
f[1] = f[0] = 1;
scanf ("%d", &n);
for (int i = 2; i <= n; i++)
for (int j = 0; j < i; j++)
f[i] += f[j] * f[i-j-1];
printf("%lld\n", f[n]);
}
/**
记忆化
**/
#include <cstdio>
long long f[16];
long long function (int n) {
if (n <= 1) return 1;
if (!f[n])
for (int i = 0; i < n; i++)
f[n] += function(i) * function(n-1-i);
return f[n];
}
int main () {
int n;
f[1] = f[0] = 1;
scanf ("%d", &n);
printf("%lld\n", function(n));
}
位数问题
【问题描述】
在所有的N位数中,有多少个数中有偶数个数字3?由于结果可能很大,你只需要输出这个答案对12345取余的值。
【输入】
读入一个数N(N≤1000)
【输出】
输出有多少个数中有偶数个数字3。
【输入样例】
2
【输出样例】
73
根据题目分析,假定f(n)表示位数为n的数中偶数个3的情况,t(n)表示位数为n的数中奇数个3的情况。
将问题的规模缩小一步考虑,实际上当前f[n]是由2部分组成,即n-1位数中所有偶数个3的情况乘以9(可以在每一位后面添加0、1、2、4、5、6、7、8、9),和n-1位数中所有奇数个3的情况乘以1(在后面添加3)。而奇数的3的情况也类似,那么递推式就出来了
f(n) = f(n-1) × 9 + t(n-1)
t(n) = t(n-1) × 9 + f(n-1)
需要注意的是,n=1,和n=2的情况单独考虑,因为n=1是0被考虑在内,而n=2的情况中,0是不能放在首位的。
参考程序
#include <cstdio>
#define N 1005
#define K 12345
int t[N], f[N];
int main () {
int n;
scanf ("%d", &n);
t[1] = 1, f[1] = 9;
t[2] = 17, f[2] = 73;
for (int i = 3; i <= n; i++) {
t[i] = (f[i-1] + t[i-1]*9) % K;
f[i] = (t[i-1] + f[i-1]*9) % K;
}
printf("%d\n", f[n]);
}
总结
- 递推方程实际上是一个数学方程。而我们是通过将问题划分为不同的阶段,找到各个阶段之间的练习的方式推导出来的。
- 对于方程的推导。一般采用降维处理,考虑最后一步和哪些状态有联系。
- 递推的很多公式推导都是乘法原理(分步完成)和加法原理(分类完成)的使用。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号