递归
算法笔记第一期
递归
在学习递归之前,首先应该掌握的是函数的相关知识,如何定义以及调用函数。函数的作用在于
- 代码重用
- 问题分解
并且能够一定程度上体会模块化编程的思想。
递归实际上也是一种函数的应用。函数自己调用自己,这种调用称为“递归”。这种函数被称为“递归函数”。
观察以下程序,思考输出结果
#include <cstdio>
void function (int n) {
if (n > 0) {
function(n-1);
for(int i = 1; i <= n; i++)
printf ("#");
printf("\n");
}
}
int main () {
function(5);
return 0;
}
以上明显存在自我调用,因此是递归函数,上面函数执行过程如下图

每一次函数的调用,都会被存入系统栈空间。函数终止条件为n<=0,当到达使得n==0的调用函数,才会停止继续调用自身,返回上一次调用也就是function(1),接下来执行for循环语句,执行完该次调用,返回到function(2),继续执行for循环,依次类推,执行到function(5)。
递归思想
根据之前的例子,可以发现一个问题想用递归函数来解决,需要满足两个条件:
1、可以将原问题转换为一个新问题,新问题的解法相同于原问题,只是问题的规模缩小
2、递归函数要明确一个终止条件,在到达终止条件的的时候递回。
例1、阶乘的求法
题目描述:
输入一个n,用递归的方式求出n的阶乘(1<n<10),并输出答案。(n! = n×(n-1)×(n-2)…2×1)
例如,输出 5,输出 120
问题分析:
n! = n × (n-1)!
根据上面的分析结果来看,对于n的阶乘问题,我们可以转化为(n-1)的阶乘问题,同理(n-1)的阶乘可以转换为(n-2)的阶乘,这样问题的规模在不断缩小,直到1,结束递归。
递归关系式可以被表示如下
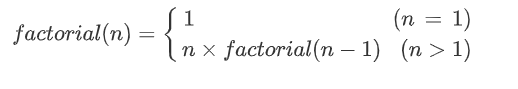
#include <cstdio>
int factorial (int n) {
if (n == 1)
return 1;
return n * factorial(n-1);
}
int main () {
int n;
scanf ("%d", &n);
printf("%d", factorial(n));
return 0;
}
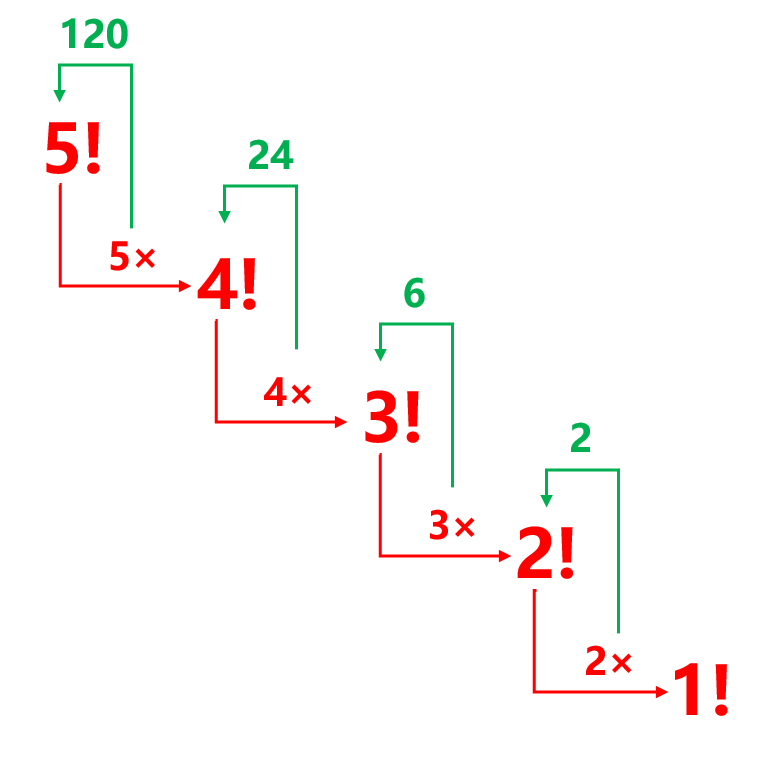
用5的阶乘作为例子,上述递归代码执行过程可表示为下图,当n=1时,出现边界,开始返回
题目练习
1.求斐波那契数列的第n项
输入n,按照斐波那契数列,输出第n项的大小(0<n<40)
参考程序
#include <cstdio>
int fibonacci (int n) {
if (n == 1)
return 1;
if (n == 2)
return 1;
return fibonacci(n-1) + fibonacci(n-2);
}
int main () {
int n;
scanf ("%d", &n);
printf("%d", fibonacci(n));
return 0;
}
2.数的倒序
输入一个非负整数n(int范围内),使用递归的方法输出这个数的倒序结果(保留前置0)。
参考程序
#include <cstdio>
void reverse (int n) {
if (n) {
printf("%d", n%10);
reverse(n/10);
}
}
int main () {
int n;
scanf ("%d", &n);
reverse(n);
return 0;
}
3.将10进制的数转化为8进制的数
参考程序
#include <cstdio>
void convert (int n, int r) {
if (n == 0)
return ;
convert (n/r, r);
printf("%d", n%r);
}
int main () {
int n;
scanf ("%d", &n);
convert(n, 8);
return 0;
}
小结
采用“递归”思路解决问题的方法都是递归算法。
算法适用场景:
- 数据的定义形式上是递归的,例如阶乘
- 问题的解法是重复执行某种操作的,并且问题规模在缩小,有明显的边界。例如最大公约数、汉诺塔
- 数据之间的逻辑关系是递归的,例如树、图的定义和操作
使用递归算法要注意的几点:
- 明确递归终止条件(边界)
- 给出递归终止的处理办法
- 提取重复逻辑,缩小问题规模
巩固训练
1.求取最大公约数
输入两个正整数m、n,求m和n的最大公约数(2000 > m,n > 1)
例如输入
56 48
输出
8
采用辗转相除法进行处理,又称为欧几里德算法。过程是做除法运算,通过除数和余数反复做除法运算,当余数为0时,取当前算式除数为最大公约数。
例如求76和58的最大公约数
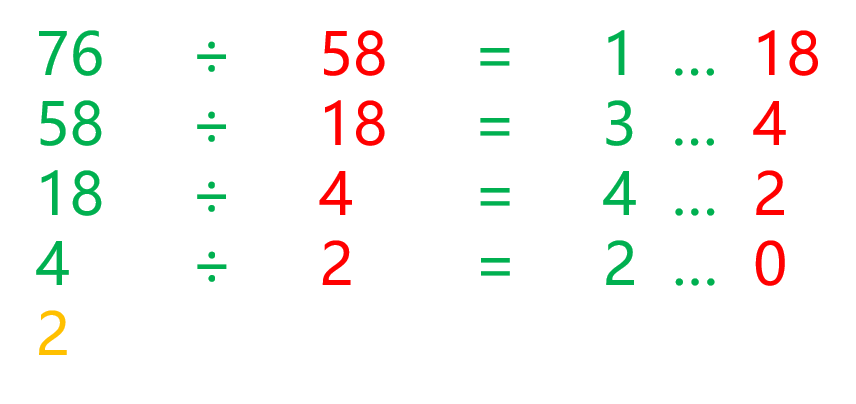
根据辗转相除的结果,当余数为0时,那么2就是76和58的最大公约数,根据递归的思路(m,n)的最大公约数和(n, m%n)的最大公约数相同,问题规模缩小了,可以得出递归公式如下
参考程序
#include <cstdio>
int gcd (int m, int n) {
if (n == 0) return m;
return gcd(n, m % n);
}
int main () {
int m, n;
scanf ("%d %d", &m, &n);
printf("%d\n", gcd(m, n));
return 0;
}
2.质因子分解
输入一个正整数n,从小到大输出它的所有质因子 (1<n<100000)
例如输出 18
输出 2 3 3
思路:从2开始试除,因为2是最小的质因子,如果2是n的因子,那么将问题转换为n/2,如果2不是n的因子,尝试3,依次类推,直到n被除成1为止。
参考程序
#include <cstdio>
void prime_factor (int n, int k) {
if (n == 1)
return;
if (n % k == 0) {
printf("%d ", k);
prime_factor(n/k, k);
} else
prime_factor(n, k+1);
}
int main () {
int n;
scanf ("%d", &n);
prime_factor(n, 2);
return 0;
}
3.分解因数
给定一个正整数a,要求分解成若干个正整数的乘积,即a = a1 × a2 × a3 × .... × an,并且 1 < a1 <= a2 <= a3 <= ... <= an。求这样的分解总数有多少,a=a也是一种分解
【输入】
第1行是测试数据的组数n,后面跟着n行输入。每组测试数据占1行,包括一个正整数a(1<a<32768)。
【输出】
n行,每行输出对应一个输入。输出应是一个正整数,指明满足要求的分解的种数。
【输入样例】
2
2
20
【输出样例】
1
4
注意考虑到本身也是一种分解情况。有些类似上一题,但不相同,计算出一个因子数可以进行加1操作,每次递归时,可以先将本身的情况算进去,如果本身是质数,那么要做出加1 的操作并且要结束分解。
参考程序
#include <cstdio>
int function (int n, int k) {
int ans = 1; //算上本身这种情况
for (int i = k; i*i <= n; i++) { // i*i<=n 相当于边界
if (n % i == 0) {
ans += function(n/i, i);
}
}
return ans;
}
int main () {
int n, number;
scanf ("%d", &n);
for (int i = 1; i <= n; i++) {
scanf ("%d", &number);
printf("%d\n", function(number, 2));
}
return 0;
}
4.数的计算
【题目描述】
我们要求找出具有下列性质数的个数(包括输入的自然数n)。先输入一个自然数n(n≤1000),然后对此自然数按照如下方法进行处理:
不作任何处理;
在它的左边加上一个自然数,但该自然数不能超过原数的一半;
加上数后,继续按此规则进行处理,直到不能再加自然数为止。
【输入】
自然数n(n≤1000)。
【输出】
满足条件的数
【输入样例】
6
【输出样例】
6
对于6,满足条件的有6,16,26,36,126,136。如果f(6)表示6的计数情况,显然f(6) = f(1)+f(2)+f(3)+1,意思是当前数字的前一半的情况之和等于当前这个数的计数,加1是表示本身。很明显可以使用递归。每次除2操作后产生的数只要大于1 都可以计入总和。需要注意的是n可能有1000个,在我们递归的过程中可能出现重复计算例如计算f(24),在缩减规模的时候,f(6)会被计算多次,这样产生相当大的浪费,于是可以将每一个数字的计数情况记录在bin数组中,这样当我们需要缩小规模的时候,如果f(n)已经被计算过来,直接从数组中取出即可。这样做也叫做记忆化。
参考程序
#include <cstdio>
#define N 1005
int bin[N];
int number_count (int n) {
int ans = 1;
for (int i = 1; i <= n / 2; i++) {
if (!bin[i])
bin[i] = number_count(i);
ans += bin[i];
}
return ans;
}
int main () {
int n;
scanf ("%d", &n);
printf("%d\n", number_count(n));
return 0;
}
总结
为什么递归能够缩减问题规模?
因为递归就是通过不断改变函数的参数,从而逼近触发“递归终止条件”,这个过程中使得问题大事化小、小事化了。因此要能够总结出正确的递归关系式和终止条件
递归的缺点:
- 重复计算,因此算法效率较低
- 递归条件不适当的情况下,容易出现死循环和栈溢出,因此递归深度是有限的。
- 递归中不要定义局部数组(容易爆栈)
加深训练
1.汉诺塔
【问题描述】
约19世纪末,在欧州的商店中出售一种智力玩具,在一块铜板上有三根杆,最左边的杆上自上而下、由小到大顺序串着由64个圆盘构成的塔。目的是将最左边杆上的盘全部移到中间的杆上,条件是一次只能移动一个盘,且不允许大盘放在小盘的上面。
假定圆盘从小到大编号为1, 2, ...
【输入】
输入为一个整数(小于20)后面跟三个单字符字符串。
整数为盘子的数目,后三个字符表示三个杆子的编号。
【输出】
输出每一步移动盘子的记录。一次移动一行。
每次移动的记录为例如 a->3->b 的形式,即把编号为3的盘子从a杆移至b杆。
【输入样例】
2 a b c
【输出样例】
a->1->c
a->2->b
c->1->b
思路:假设有n个盘子要从a柱移动到b柱,那么考虑到问题规模缩小,将从上到下的n-1个盘子看出一个整体,那么需要做的是将n-1个盘子一起移动到c柱上,然后将a上的n号盘子移动到b上,最后将c柱上的n-1个盘子移动回b柱。这样就完成了整体的移动。
参考程序
#include <cstdio>
void hanoi (int n, char a, char b, char c) { //表示将n个盘子从a移动到b 借助c
if (n == 0)
return;
hanoi(n-1, a, c, b);
printf("%c->%d->%c\n", a, n, b);
hanoi(n-1, c, b, a);
}
int main () {
int n;
char A, B, C;
scanf("%d %c %c %c", &n, &A, &B, &C);
hanoi(n, A, B, C);
return 0;
}
2. 2的幂次方表示
【问题描述】
任何一个正整数都可以用2的幂次方表示。例如:
137=27+23+2^0
同时约定方次用括号来表示,即ab可表示为a(b)。由此可知,137可表示为:
2(7)+2(3)+2(0)
进一步:7=22+2+20(21用2表示)
3=2+2^0
所以最后137可表示为:
2(2(2)+2+2(0))+2(2+2(0))+2(0)
又如:
1315=210+28+2^5+2+1
所以1315最后可表示为:
2(2(2+2(0))+2)+2(2(2+2(0)))+2(2(2)+2(0))+2+2(0)
【输入】
一个正整数n(n≤20000)。
【输出】
一行,符合约定的n的0,2表示(在表示中不能有空格)。
【输入样例】
137
【输出样例】
2(2(2)+2+2(0))+2(2+2(0))+2(0)
思路:幂次方分解明显是递归的思想。由于n的最大为20000,2的15次方已经超过这个数了,因此可以将2的0到15次方存在数组b中,下标表示幂,b[0]表示2的0次方,b[2]表示2的2次方。这样便于从最接近n的幂开始寻找,找到第一个后n缩小为n-b[i]。然后将下标作为n继续分解。其中由于有+号需要注意如何利用全局变量,保证在递归回来后输出。
参考程序
#include <cstdio>
int b[16];
bool flag = true;
void init () {
b[0] = 1;
for (int i = 1; i < 16; i++)
b[i] = b[i-1] * 2;
}
void power (int n) {
while (n) //将当前的n全部分解完
for (int i = 15; i >= 0; i --) { //找到最接近n的2的幂
if (b[i] <= n) {
n -= b[i];
if (flag) flag = false;
else printf("+");
if (i > 1) {
printf("2(");
flag = true;
power(i);
printf(")");
}
if (i == 1) //边界条件
printf("2");
else if (i == 0) //边界条件
printf("2(0)");
}
}
}
int main () {
init ();
int n;
scanf ("%d", &n);
power(n);
return 0;
}
3.放苹果
【问题描述】
把M个同样的苹果放在N个同样的盘子里,允许有的盘子空着不放,问共有多少种不同的分法?(用K表示)5,1,1和1,5,1 是同一种分法。
【输入】
第一行是测试数据的数目t(0≤t≤20)。以下每行均包含二个整数M和N,以空格分开。1≤M,N≤10。
【输出】
对输入的每组数据M和N,用一行输出相应的K。
【输入样例】
1
7 3
【输出样例】
8
思路:
难点在于,找到递归关系式。首先考虑加入盘子的数量多于苹果的数量,那么势必会有空盘。并且空盘的数量至少是n-m。这些空盘都是无用的。
其次,对于m个苹果,n个盘子。总的情况中可以分为2类,第一类每个盘子至少有一个苹果,第二类至少有一个空盘。这两种情况,那么对于f(m,n),第一类只考虑每个盘子至少有一个苹果的情况数量,和从每个盘子拿一个苹果出来的情况数量是相同即f(m,n) = f(m-n, n),而第二类至少有一个空盘的情况,和将这个空盘拿走的情况数量是相同的,即f(m,n) = f(m, n-1)。将这两种情况组合就是总的情况。即f(m,n) = f(m-n,n) + f(m, n-1)。其中递归终点很显然,是盘子为1或者苹果数为0的时候只有一种情况。
参考程序
#include <cstdio>
int put_apple (int m, int n) {
if (n > m)
n = m;
if (n == 1 || m == 0)
return 1;
return put_apple (m-n, n) + put_apple (m, n-1);
}
int main () {
int t, m, n;
scanf ("%d", &t);
while (t --) {
scanf("%d %d", &m, &n);
printf("%d\n", put_apple(m, n));
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号