埃拉托色尼筛选法(素数筛选法)

素数指的是在一个大于1的自然数中,除了1和此整数自身以外 ,不能被其他自然数整除.在加密应用中起重要的位置，比如广为人知的RSA算法中，就是基于大整数的因式分解难题，寻找两个超大的素数然后相乘作为密钥的。一个比较常见的求素数的办法是埃拉托斯特尼筛法(the Sieve of Eratosthenes) ，说简单一点就是画表格，然后删表格，如图所示：

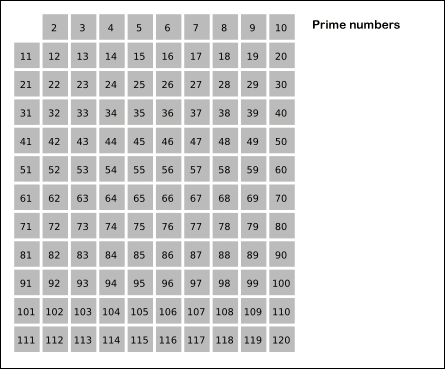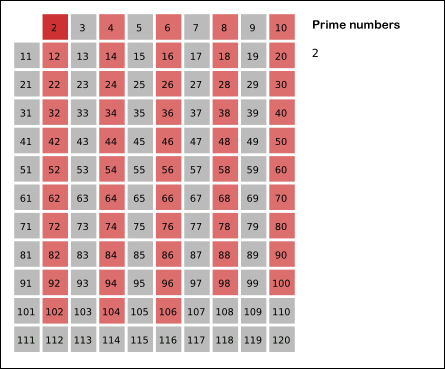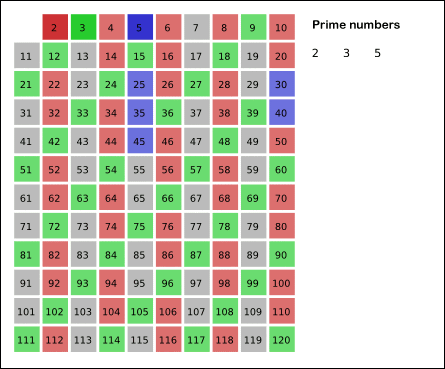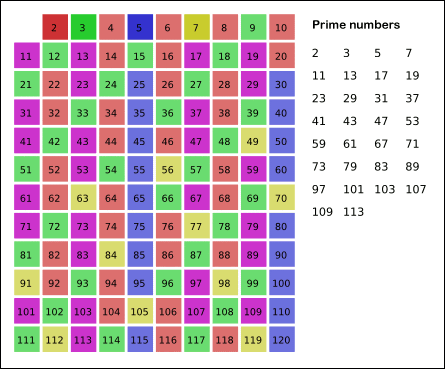
 具体思想就是:先将1去掉,将2的倍数去掉,将3的倍数去掉,.......,将i的倍数去掉,一直到A

Python实现:

#!/usr/bin/python
num=100
arr=[True]*(num+1)
#第一个素数
n=2
while n*n <= num:
    if arr[n]:
               #试下n*n行不行
        for i in range(n*2,num+1,n):
            arr[i]=False
        n+=1
#打印所有素数
print([element for  element in range(2,num) if arr[element]])#得到小于num的素数
#打印小于num,素数的个数,需要去掉0和1
print(arr.count(True)-2)