[LuoguP1801] 黑匣子

题目描述

Black Box是一种原始的数据库。它可以储存一个整数数组，还有一个特别的变量i。最开始的时候Black Box是空的．而i等于0。这个Black Box要处理一串命令。

命令只有两种：

ADD(x):把x元素放进BlackBox;

GET:i加1，然后输出Blackhox中第i小的数。

记住：第i小的数，就是Black Box里的数的按从小到大的顺序排序后的第i个元素。例如：

我们来演示一下一个有11个命令的命令串。（如下图所示）

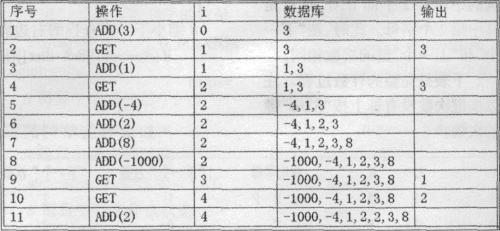
现在要求找出对于给定的命令串的最好的处理方法。ADD和GET命令分别最多200000个。现在用两个整数数组来表示命令串：

1.A(1)，A(2)，…A(M)：一串将要被放进Black Box的元素。每个数都是绝对值不超过2000000000的整数，M$200000。例如上面的例子就是A=(3，1，一4，2，8，-1000，2)。

2.u(1)，u(2)，…u(N)：表示第u(j)个元素被放进了Black Box里后就出现一个GET命令。例如上面的例子中u=(l，2，6，6)。输入数据不用判错。

输入格式

第一行，两个整数，M，N。

第二行，M个整数，表示A(l)

……A(M)。

第三行，N个整数，表示u(l)

…u(N)。

输出格式

输出Black Box根据命令串所得出的输出串，一个数字一行。

输入输出样例

输入 #1复制

7 4
3 1 -4 2 8 -1000 2
1 2 6 6

输出 #1复制

3
3
1
2

说明/提示

对于30%的数据，M≤10000;

对于50%的数据，M≤100000：

对于100%的数据，M≤200000。

 

一个大根堆维护前i个

一个小根堆维护剩下的

也可以直接平衡树

 

#include <bits/stdc++.h>
using namespace std;
priority_queue<int> q1;
priority_queue<int, vector<int>, greater<int> > q2;
int m, n;
int a[200000 + 10], u[200000 + 10];
int main(){
    cin >> m >> n;
    for(int i = 1; i <= m; i++) cin >> a[i];
    for(int i = 1; i <= n; i++) cin >> u[i];
    for(int i = 1; i <= u[1]; i++){
        q2.push(a[i]);
    }
    cout << q2.top() << endl;
    for(int i = 2; i <= n; i++){
        q1.push(q2.top()); q2.pop();
        for(int j = u[i - 1] + 1; j <= u[i]; j++){
            q1.push(a[j]);
            q2.push(q1.top());
            q1.pop();
        }
        cout << q2.top() << endl;
    }
    return 0;
}