2020hdu多校第七场比赛及补题

1009 Increasing and Decreasing

一个n的全排列，它的最长上升子序列长度为x，它的最长下降子序列长度为y，让你构造一个这样的字典序最小的全排列

这签到题好难，我也只是猜出来的结论，也不怎么清楚怎么证明，我的思路就是分为 x 个下降子序列,比如x=3,y=5时，若n = 15我构造出来的是 5 4 3 2 1   10 9 8 7 6   15 14 13 12 11,若n = 14,我构造出来的是 4 3 2 1   10 9 8 7 6   15 14 13 12 11，就是这种构造法

#include<iostream>
#include<algorithm>
using namespace std;
const int MAXN = 1e5+7;
int ans[MAXN];
int lolo[MAXN];
int main()
{
	int T, n, x, y;
	cin >> T;
	while(T--){
		cin >> n >> x >> y;
		if(x+y>n+1){
			cout<<"NO"<<endl;
			continue;
		}
		for (int i = 1;i <= n;i++) ans[i] = 0;
		bool flag = false;
		int cnt = 0;
		int lis = 0;
		int cs = n/y;
		if(y * cs < n) cs++;
		if(x < cs){
			cout<<"NO"<<endl;
			continue;
		} 
		int su = n - x; 
		for(int i = 1;i <= x;i++){
			lolo[i] = 1;
		}
		for(int i = x;i;i--){
			if(su >= y - 1){
				su -= y - 1;
				lolo[i] += y - 1;
			}
			else if(su){
				lolo[i] += su;
				su = 0;
			}
			else break;
		}
		int pos = 0;
		for(int i = 1;i <= x;i++){
			for(int j = 1;j <= lolo[i];j++){
				pos++;
				ans[pos] = cnt + lolo[i] - j + 1;
			}
			cnt += lolo[i];
			//cout<<lolo[i]<<endl;
		}
		cout<<"YES"<<endl;
		for(int i = 1;i < n;i++){
			printf("%d ",ans[i]);
		}
		printf("%d\n",ans[n]);
	}
	return 0;
} 

　　

1010 Jogging

一个无限大的二维地图，一个格子坐标为（x,y），若x,y互质，那这个格子就是墙，否则这个格子就是一个空地

现给一个初始坐标，每次跳远可以等概率的跳到周围八格的空地和自身的格子里（周围八格有z格空地，那跳到这z格的概率分别为1/(z+1),跳到自己身上的一格的概率也是1/(z+1) ）

问跳跃无数次后，回到初始坐标的概率

分析：

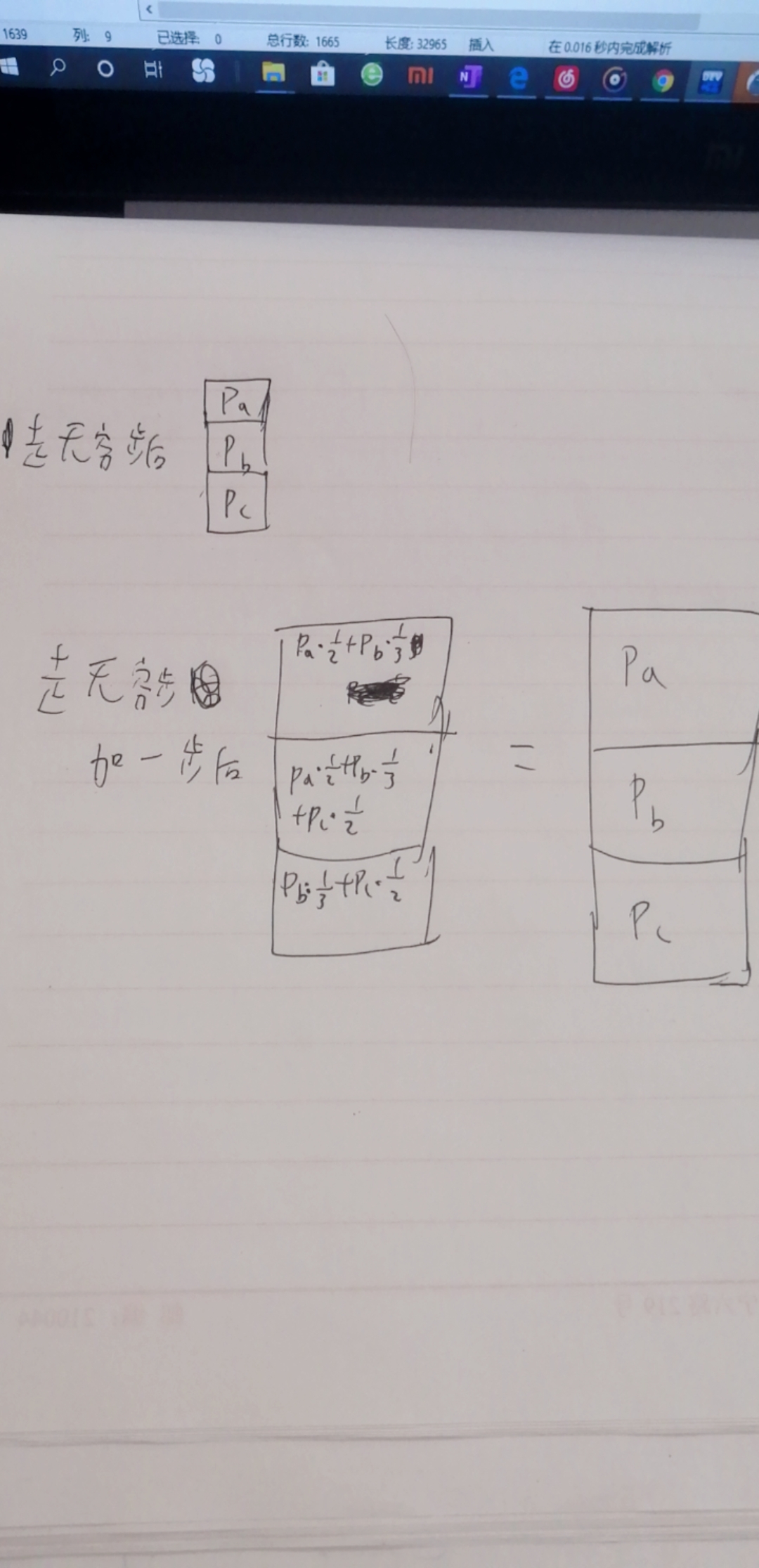
• 首先，坐标互质的格子为墙，其余为空地，和一个叫恐怖稽器人的题一样，有着一些性质：
• 1、对角线上的格子，除了(1,1),全是空地，所以如果可以跳到对角线，那么就可以跳到对角线上所有的格子（无限）
• 2、如果不能跳到对角线，那么可以跳到的格子是很有限的
• 上面的两个性质可以把一部分地图输出出来，观察得到,那么如果能跳到对角线，回到初始坐标的概率就为0，如果周围八格都是墙，概率为1，else,概率为0到1之间的分数

计算：

概率为（0,1]时，该怎么计算这个概率，我做的时候感觉自己算不来，因为我概率题没学过，就先看其他题了，没多想这个，虽然没多想，但我还是观察到一个东西的，在一个样例中：

1号格子能跳到1号，2号 

2号格子能跳到1号，2号，3号

3号格子能跳到2号，3号

初始坐标在1号格子

样例的答案时2 / 7

1号格子能跳到2个格子

2号格子能跳到3个格子

3号格子能跳到2个格子

2 / 2 + 3 + 2恰好等于 2 / 7

当时我感觉应该不是这么简单的，后来突然想要判断这个计算方法是否正确

然后我还真的证出就是这样算的

#include<iostream>
#include<algorithm>
using namespace std;
bool vis[400][400];
long long res[400][400];
long long opx[8] = {-1,-1,-1,0,0,1,1,1};
long long opy[8] = {-1,0,1,-1,1,-1,0,1};
long long gcd(long long a,long long b){
	if(a<b) swap(a,b);
	while(b){
		a = a % b;
		swap(a,b);
	}
	return a;
}
int fz,fm;
long long sx, sy;
bool flag;
void dfs(long long xx,long long yy){
	vis[200+xx][200+yy] = true;
	res[200+xx][200+yy] = 1;
	for(int i = 0;i < 8;i++ ){
		long long dx = xx + opx[i], dy = yy + opy[i];
		if(gcd(sx + dx,sy + dy) > 1){
			res[200+xx][200+yy]++;
			if(vis[200+dx][200+dy]) continue;
			if(sx + dx == sy + dy){
				flag = false;
				return;
			} 
			dfs(dx,dy);
			if(sx + dx == sy + dy){
				flag = false;
				return;
			} 
		}  
	}
	//cout<<res[200+xx][200+yy]<<endl;
	fm += res[200+xx][200+yy];
}
int main()
{

	int T;
	cin >> T;
	while(T--){
		cin>>sx>>sy;
		fz = fm = 0;
		for(int i = 0;i < 400;i++){
			for(int j = 0;j < 400;j++){
				vis[i][j] = false;
				res[i][j] = 0;
			}
		}
		flag = true;
		dfs(0,0);
		if(!flag) {
			cout<<"0/1"<<endl;
			continue;
		}
		fz = res[200][200];
		long long g = gcd(fz,fm);
		fz /= g;fm /= g;
		cout<<fz<<"/"<<fm<<endl;
	}
	return 0;
}

　　

 1004 Decision

 难的一匹OAO，补题补了好久

题意：给定t,a,c,m。2t<=m

u,v是在[0,t]范围内的随机的数(取各个数字的概率相同)，X[0] = u + v, X[i] = (X[i-1] * a + c) % m (i >= 1),如果X[ | u-v| ] 为偶数则获胜,问获胜的概率

看到这个，我是想到会成一个环，然后自己就开始写了，写了好长，然后样例都过不了，才发现这不是一个环

看了题解才知道这是一个环套树森林，我自己写的代码又长又烂又错的离谱,看了下std，很短很简洁orz, 果然acmer与acmer是不能一概而论的

正解是倍增，这种思路我很少用到，写的时候把人写傻了

#include<iostream>
#include<algorithm>
using namespace std;
const int MAXN = 1e6+7;
int fa[20][MAXN];
long long dp[20][MAXN];
long long fz,fm;
void cnt(int p,int k){ 
	for(int i = 19;i >= 0;i--){
		if((1<<i)>k) continue;
		fz += dp[i][p] * 2;
		k -= 1<<i;
		p = fa[i+1][p];
	}
}
long long gcd(long long a,long long b){
	if(a<b) swap(a,b);
	while(b){
		a = a % b;
		swap(a,b);
	}
	return a;
}
int main()
{
	int T;
	cin>>T;
	long long t,a,c,m;
	while(T--){
		cin>>t>>a>>c>>m;
		fz = 0;
		for(long long i = 0;i < m; i++) {
			fa[0][i] = (i * a + c) % m;
			dp[0][i] = (fa[0][i] % 2 == 0);
		}
		for(int i = 1;i < 20; i++){
			for(int j = 0;j < m;j++){
				fa[i][j] = fa[i-1][fa[i-1][j]];
				dp[i][j] = dp[i-1][j] + dp[i-1][fa[i][j]];
			}
		}	
		for(int i = 0;i <= t;i++){
			if(i%2) cnt(i,i/2+1);
			else {
				fz++;
				cnt(fa[0][i],i/2);
			}
		}
		for(int i = t + 1;i <= 2 * t;i++){
			if(i%2) cnt(i,(2 * t - i) / 2 + 1);
			else {
				fz++;
				cnt(fa[0][i],(2 * t - i) / 2);
			} 
		}
		fm = (t+1)*(t+1);
		long long gg = gcd(fz,fm);
		fz/=gg;fm/=gg;
		cout<<fz<<"/"<<fm<<endl;
	}
	return 0;
}