【翻译】Species distribution modeling 5 模型拟合、预测、评价

5.1 模型拟合

　　模型拟合与存在于R中的建模方法在技术上十分相似。大多数方法使用formula来识别独立和依赖性变量，伴随着一个包含这些变量的data.frame。有关具体方法的详细信息，请参见本文档第三部分。

　　一个简单的公式可能看起来像：y ~ x1 + x2 + x3 ，也就是说，y是x1，x2和x3的函数。另一个离子是 y ~ .，这意味着y是提供给函数的data.frame中所有其他参数的函数。参见help('formula')查看有关公式语法的更多细节。在下方的例子中，函数glm被用来拟合一般线性模型。glm返回一个模型对象。

　　注意下方的例子，我们又一次使用‘sdmdata’这个data.frame。首先从磁盘中读取sdmdata（我们在上一章结束时保存了它）。

sdmdata <- readRDS("sdm.Rds")
presvals <- readRDS("pvals.Rds")

　　

m1 <- glm(pb ~ bio1 + bio5 + bio12, data=sdmdata)
class(m1)
## [1] "glm" "lm"
summary(m1)
##
## Call:
## glm(formula = pb ~ bio1 + bio5 + bio12, data = sdmdata)
##
## Deviance Residuals:
##      Min        1Q    Median        3Q       Max
## -0.62298  -0.23134  -0.08801   0.08069   0.92866
##
## Coefficients:
##               Estimate Std. Error t value Pr(>|t|)
## (Intercept)  1.336e-01  1.085e-01   1.232  0.21844
## bio1         1.252e-03  3.877e-04   3.229  0.00131 **
## bio5        -1.391e-03  4.716e-04  -2.950  0.00330 **
## bio12        1.381e-04  1.689e-05   8.177 1.68e-15 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for gaussian family taken to be 0.1187387)
##
##     Null deviance: 94.156  on 615  degrees of freedom
## Residual deviance: 72.668  on 612  degrees of freedom
## AIC: 441.53
##
## Number of Fisher Scoring iterations: 2

m2 = glm(pb ~ ., data=sdmdata)
m2
##
## Call:  glm(formula = pb ~ ., data = sdmdata)
##
## Coefficients:
## (Intercept)         bio1        bio12        bio16        bio17
##   0.2816158   -0.0023685    0.0004537   -0.0006286   -0.0007830
##        bio5         bio6         bio7         bio8       biome2
##  -0.0203384    0.0216124    0.0200767    0.0007421   -0.0840330
##      biome3       biome4       biome5       biome7       biome8
##  -0.0736604   -0.1090272   -0.0608034   -0.1957278   -0.0495390
##      biome9      biome10      biome11      biome12      biome13
##   0.0355491   -0.0610281   -0.3649844   -0.0503743    0.0226996
##     biome14
##  -0.0742118
##
## Degrees of Freedom: 614 Total (i.e. Null);  594 Residual
##   (1 observation deleted due to missingness)
## Null Deviance:       94.12
## Residual Deviance: 67.91     AIC: 434.2

　　在dismo中实施的模型不使用公式（而且大多数模型只有存在点）。Bioclim是一个例子。它只用存在数据，所以我们使用‘presvals’代替‘sdmdata’。

bc <- bioclim(presvals[,c('bio1', 'bio5', 'bio12')])
class(bc)
## [1] "Bioclim"
## attr(,"package")
## [1] "dismo"
bc
## class    : Bioclim
##
## variables: bio1 bio5 bio12
##
##
## presence points: 116
##    bio1 bio5 bio12
## 1   263  338  1639
## 2   263  338  1639
## 3   253  329  3624
## 4   243  318  1693
## 5   243  318  1693
## 6   252  326  2501
## 7   240  317  1214
## 8   275  335  2259
## 9   271  327  2212
## 10  274  329  2233
##   (... ...  ...)
pairs(bc)

　　

5.2 模型预测

　　不同的建模方法返回不同类型的‘model’对象（通常它们具有与使用的建模方法相同的名称）。所有这些‘model’对象，不管它们的确切类（class），可以被用于使用predict函数来对任何独立参数所组成的值来作出预测。下方的例子演示了我们使用glm模型对象‘m1’和bioclim模型中的‘bc’来作出预测，对于变量bio1、bio5和bio12的三个记录（这些变量在上方的例子中被用于创建模型对象）。

bio1 = c(40, 150, 200)
bio5 = c(60, 115, 290)
bio12 = c(600, 1600, 1700)
pd = data.frame(cbind(bio1, bio5, bio12))
pd
##   bio1 bio5 bio12
## 1   40   60   600
## 2  150  115  1600
## 3  200  290  1700
predict(m1, pd)
##         1         2         3
## 0.1830781 0.3823152 0.2152447
predict(bc, pd)

　　对少量环境作出这种预测对于探索和理解模型预测是很有用处的。例如，它在函数response中使用，将其它参数设为中值来创建每个参数的响应图形。

　　大多数情况下，无论如何，SDM的意图都是创建一个适应性分数的地图。我们可以利用一个Raster*对象和一个模型对象来提供预测函数。只要模型对象中的参数名在Raster*对象的图层（layerNames）中是可用的。

predictors <- stack(list.files(file.path(system.file(package="dismo"), 'ex'), pattern='grd$', full.names=TRUE ))
names(predictors)
## [1] "bio1"  "bio12" "bio16" "bio17" "bio5"  "bio6"  "bio7"  "bio8"  "biome"
p <- predict(predictors, m1)
plot(p)

　　

5.3 模型评价

　　相对于评估一个模型的好坏和它是否可以用于一个特定的目的来说，去创建模型和作出预测就太简单了。大多数模型都有不同的量度来帮助评估模型与数据的适宜度。熟悉这些并了解它们的角色是值得的，因为它们帮助你去评估你的模型是否有实质性的错误。大多数统计或机器学习的说明（texts）都会提供一些细节。例如，对于GLM来说，可以查看解释了多少偏差，有没有残差模式，有没有高杠杆点等。然而，自从很多模型被用于预测，更多的评价集中于模型对于在模型训练中没有使用的点的预测程度。（参见有关数据分区的下一节）。在我们给出用于评价的统计的例子之前，应当考虑的是在评价一个模型时还需要做什么。有用的问题包括：
　　模型在生态学意义上看起来是合理的吗？
　　拟合函数（建模关系的性状）合理吗？
　　这些预测看起来合理吗（绘制成地图，然后考虑它们）？
　　在模型残差中有任何空间模式吗（参见Leathwick and Whitehead 2001作为一个有趣的例子）？

　　大多数建模依赖交叉验证。这包括创建包含一个‘training’数据集的模型，然后用另一个包含已知出现点的数据集测试它。典型地，训练和测试数据是通过从一个单独的数据集随机抽样（无需替换）获得的。仅仅在少数情况下，比如Elith et al., 2006，训练和测试数据来自不同的源并预先定义好了。

　　可以使用不同的措施评估预测的质量（Fielding and Bell，1997，Liu et al., 2011；and Potts and Elith（2006）为丰富数据），也许取决于研究的目标。许多对基于存在-不存在数据或仅存在数据的模型的评估措施是‘阈值依赖（threshold dependent）’的。那意味着必须首先设定一个阈值（比如0.5，尽管0.5很少是一个明智的选择-见Lui et al.2005的例子）。超过阈值的预测值表示一个‘存在’的预测，而低于阈值表示‘不存在’。一些措施注重虚假（false）不存在的比重；其他的把更多比重放在虚假存在。

　　大量使用与阈值无关的统计信息都是相关系数和接收器操作曲线之下的区域（AUROC，通常进一步缩写为AUC）。AUC是一个级别相关的量度。在无偏差的数据中，一个高的AUC代表着具有高预测适用性值的场所往往是已知存在的区域，而具有较低模型预测值的地点往往是物种未知存在的区域（不存在或者随机点）。一个0.5分的AUC意味着模型与随机猜测一样好。关于在仅存在而不是存在/不存在数据的情况下使用AUC的讨论见Philips et al. (2006)。

　　这里我们可视化了相关系数的计算和两个随机参数的AUC。p（presence）具有更高的值，而且代表着物种所存在的50个已知情况（地点）的预测值，而a（absence）具有较低的值，而且代表着物种所不存在的50个已知情况（地点）的预测值。

p <- rnorm(50, mean=0.7, sd=0.3)
a <- rnorm(50, mean=0.4, sd=0.4)
par(mfrow=c(1, 2))
plot(sort(p), col='red', pch=21)
points(sort(a), col='blue', pch=24)
legend(1, 0.95 * max(a,p), c('presence', 'absence'),
          pch=c(21,24), col=c('red', 'blue'))
comb <- c(p,a)
group <- c(rep('presence', length(p)), rep('absence', length(a)))
boxplot(comb~group, col=c('blue', 'red'))

　　

　　我们建立了两个具有随机正态分布值的变量，但具有不同的平均值和标准偏差。两个参数显然具有不同的分布，而‘存在’值往往更高于‘不存在’的值。以下是如何计算相关系数和AUC。

group = c(rep(1, length(p)), rep(0, length(a)))
cor.test(comb, group)$estimate
##       cor
## 0.3375294
mv <- wilcox.test(p,a)
auc <- as.numeric(mv$statistic) / (length(p) * length(a))
auc
## [1] 0.6872

　　下面我们展示如何使用dismo包中的evaluate函数计算这些和其他更方便的统计。看见了吗？评估有关可用的其他评估措施的信息。ROC/AUC也可以使用ROCR包来计算。

e <- evaluate(p=p, a=a)
class(e)
## [1] "ModelEvaluation"
## attr(,"package")
## [1] "dismo"
e
## class          : ModelEvaluation
## n presences    : 50
## n absences     : 50
## AUC            : 0.6872
## cor            : 0.3375294
## max TPR+TNR at : 0.3449397
par(mfrow=c(1, 2))
density(e)
boxplot(e, col=c('blue', 'red'))

　　

　　回到一些真实的数据上，本例中的仅存在数据。我们将此数据划分成两个随即集，一个用来培养（training）BioClim模型，另一个用来评价这个模型。

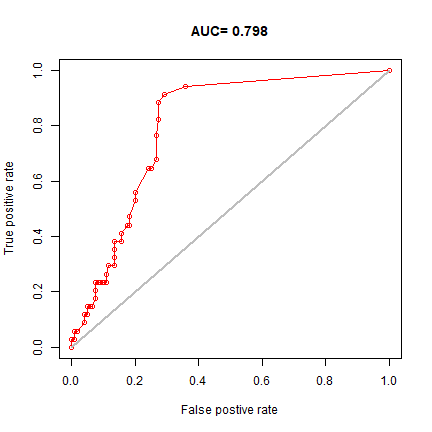
samp <- sample(nrow(sdmdata), round(0.75 * nrow(sdmdata)))
traindata <- sdmdata[samp,]
traindata <- traindata[traindata[,1] == 1, 2:9]
testdata <- sdmdata[-samp,]
bc <- bioclim(traindata)
e <- evaluate(testdata[testdata==1,], testdata[testdata==0,], bc)
e
## class          : ModelEvaluation
## n presences    : 26
## n absences     : 128
## AUC            : 0.79372
## cor            : 0.3991351
## max TPR+TNR at : 0.06656667
plot(e, 'ROC')

　　

　　在真实的项目里，你会想用k-fold数据分区来代替一个独立随即样本。dismo包中的kfold函数有助于这种类型的分区。它创建一个向量来将数据矩阵中的每一行分配给一个组（从1到k之间）。

　　让我们首先创建存在和背景数据。

pres <- sdmdata[sdmdata[,1] == 1, 2:9]
back <- sdmdata[sdmdata[,1] == 0, 2:9]

　　背景数据将会仅被用于模型测试而且不需要被分区。我们现在将数据分为5个组。

k <- 5
group <- kfold(pres, k)
group[1:10]
##  [1] 5 1 2 5 4 1 3 4 5 3
unique(group)
## [1] 5 1 2 4 3

　　现在我们可以拟合（fit）和测试我们的模型5次。在每次运行中，5组中的对应1组的记录仅被用于评价这个模型，而其他4组仅被用于拟合（fit）这个模型。结果被保存在一个叫做‘e’的列表中。

e <- list()
for (i in 1:k) {
    train <- pres[group != i,]
    test <- pres[group == i,]
    bc <- bioclim(train)
    e[[i]] <- evaluate(p=test, a=back, bc)
}

　　我们可以从‘e’中的对象里提取一些东西，但是让我们限制自己的AUC值和“最大灵敏度之和（真阳性率（true positive rate）和特指度（specificity)（负阳性率或真阴性率(true negative rate）”阈值“spec_sens”（这有时被用作将单元设置为存在或不存在的阈值）。

auc <- sapply(e, function(x){x@auc})
auc
## [1] 0.7957391 0.7907391 0.7268333 0.8164783 0.7313478
mean(auc)
## [1] 0.7722275
sapply( e, function(x){ threshold(x)['spec_sens'] } )
## $spec_sens
## [1] 0.06441613
##
## $spec_sens
## [1] 0.09667419
##
## $spec_sens
## [1] 0.02163913
##
## $spec_sens
## [1] 0.08592151
##
## $spec_sens
## [1] 0.03215806

　　在评估SDMs时使用AUC已被批评（Lobo et al. 2008，Jiménez-Valverde 2011）。一个特别粘稠（sticky）的问题是AUC的值随着用于选择背景点的空间范围而变化。通常地，范围越大，AUC的值越高。因此，AUC的值一般有偏差而且不能被直接比对。Hijmans（2012）建议从“逐点距离采样（spatial sorting bias）”中移除“空间排序偏差（spatial sorting bias）”（从测试（testing）-存在到训练（training）-存在的距离和测试-不存在到训练-不存在的点的距离。

（以下代码经过修改）

> nr <- nrow(bradypus)
> s <- sample(nr, 0.25 *nr)
> pres_train <- bradypus[-s, ]
> pres_test <- bradypus[s, ]
> nr <- nrow(backgr)
> set.seed(9)
> s <- sample(nr, 0.25 * nr)
> back_train <- backgr[-s, ]
> back_test <- backgr[s, ]

　　

> sb <- ssb(pres_test, back_test, pres_train)
> sb[,1] / sb[,2]
        p 
0.1509002 

　　sb[,1] / sb[,2]是一个空间排序偏差（spatial sorting bias，SSB）的指标。如果没有SSB，这个值将会是1，在这些数据中它接近零，表明SSB十分强（strong）。让我们创建一个移除SSB的子样本。

> i <- pwdSample(pres_test, back_test, pres_train, n=1, tr=0.1)
> pres_test_pwd <- pres_test[!is.na(i[,1]), ]
> back_test_pwd <- back_test[na.omit(as.vector(i)), ]
> sb2 <- ssb(pres_test_pwd, back_test_pwd, pres_train)
> sb2[2] / sb2[2]
[1] 1

　　空间排序偏差现在大大减少；注意AUC是如何下降的！

> bc <- bioclim(predictors, pres_train)
> evaluate(bc, p=pres_test, a=back_test, x=predictors)
class          : ModelEvaluation 
n presences    : 29 
n absences     : 125 
AUC            : 0.7637241 
cor            : 0.2030576 
max TPR+TNR at : 0.04587701 
> evaluate(bc, p=pres_test_pwd, a=back_test_pwd, x=predictors)
class          : ModelEvaluation 
n presences    : 12 
n absences     : 12 
AUC            : 0.59375 
cor            : -0.05177002 
max TPR+TNR at : 0.05737126 
>