CS224n-作业1
0 前言
1 Softmax(10分)
(a)(5分)
对于向量$x+c$的任一维度$i$,有:
\begin{align*}
\mbox{softmax(x + c)}_i &= \frac{e^{x_i + c}}{\sum_j e^{x_j + c}} \\
&= \frac{e^c e^{x_i}}{\sum_j e^c e^{x_j}} \\
&= \frac{e^c e^{x_i}}{e^c \sum_j e^{x_j}} \\
&= \frac{e^{x_i}}{\sum_j e^{x_j}} \\
&= \mbox{softmax(x)}_i
\end{align*}
(b)(5分)
向量和矩阵分开处理:
if len(x.shape) > 1: # Matrix ### YOUR CODE HERE x = x - np.max(x, 1).reshape(-1 ,1) # 每个元素都减去所在列对应的最大值 x_exp = np.exp(x) x = x_exp / np.sum(x_exp, 1) ### END YOUR CODE else: # Vector ### YOUR CODE HERE x = x - np.max(x) x_exp = np.exp(x) x = x_exp / np.sum(x_exp) ### END YOUR CODE
也可以参考完整代码
2 神经网络基础(30分)
(a)(3分)
\begin{align*}
\frac{\partial }{\partial x} \sigma(x) &= \frac{\partial \frac{1}{1+\exp(-x)}}{\partial (1+\exp(-x))}\cdot \frac{\partial (1+\exp(-x))}{\partial x} \\
&= -\frac{1}{(1+\exp(-x))^2} \cdot (-\exp(-x)) \\
&= \frac{1}{1+\exp(-x)} \cdot \frac{\exp(-x)}{1+\exp(-x)} \\
&= \sigma(x)(1-\sigma(x))
\end{align*}
(b)(3分)
题目中已经假设,$y$的第$k$维是1,其它维度都是0。首先求$\hat{y}_k$关于每一个$\theta_i$的偏导数。其中,
\begin{align*}
\hat{y}_k = \frac{\exp(\theta_k)}{\sum_j \exp(\theta_j)}
\end{align*}
当$i=k$时,
\begin{align*}
\frac{\partial \hat{y}_k}{\partial \theta_k} &= \frac{\partial }{\partial \theta_k} \frac{\exp(\theta_k)}{\sum_j \exp(\theta_i)} \\
&= \frac{\exp(\theta_k)(\sum_j \exp(\theta_i)) - \exp(\theta_k)\exp(\theta_k)}{(\sum_j \exp(\theta_i))^2} \\
&= \frac{\exp(\theta_k)}{\sum_j \exp(\theta_i)}(1 - \frac{\exp(\theta_k)}{\sum_j \exp(\theta_i)}) \\
&= \hat{y}_k(1 - \hat{y}_k)
\end{align*}
当$i \neq k$时,
\begin{align*}
\frac{\partial \hat{y}_k}{\partial \theta_i} &= \frac{\partial }{\partial \theta_i} \frac{\exp(\theta_k)}{\sum_j \exp(\theta_j)} \\
&= \frac{0 \cdot \sum_j \exp(\theta_j) - \exp(\theta_k)\exp(\theta_i)}{(\sum_j \exp(\theta_j))^2} \\
&= -\hat{y}_k\hat{y}_i
\end{align*}
对CE进行简化,
\begin{align*}
CE(y,\hat{y}) &= -\sum_iy_i\log(\hat{y}_i) \\
&=-\log(\hat{y}_k)
\end{align*}
\begin{align*}
\frac{\partial }{\partial \theta} CE(y,\hat{y}) = -\frac{\partial }{\partial \theta} \log(\hat{y}_k)
\end{align*}
当$i=k$时,
\begin{align*}
\frac{\partial }{\partial \theta_k} CE(y,\hat{y}) &= -\frac{\partial }{\partial \theta_k} \log(\hat{y}_k) \\
&= -\frac{1}{\hat{y}_k} \cdot \hat{y}_k(1 - \hat{y}_k) \\
&= \hat{y}_k - 1
\end{align*}
当$i \neq k$时,
\begin{align*}
\frac{\partial }{\partial \theta_i} CE(y,\hat{y}) &= -\frac{\partial }{\partial \theta_i} \log(\hat{y}_k) \\
&= -\frac{1}{\hat{y}_k} \cdot (-\hat{y}_k\hat{y}_i) \\
&= \hat{y}_i
\end{align*}
(c)(6分)
参考神经网络及其训练中的1.5,向后推导即可。不同的是,前文是求损失函数关于某个权重的偏导数,这里是求损失函数关于输入$x$的偏导数。
(d)(2分)
输入层到隐层需要权重$D_x \cdot H$个,偏置项$H$个。
隐层到输出层需要权重$D_y \cdot H$个,偏置项$D_y$个。
该神经网络参数总共个$D_x \cdot H + H + D_y \cdot H + D_y$。
(e)(4分)
(f)(4分)
(g)(8分)
3 word2vec(40分)
(a)(3分)
与2(b)的证明类似,
\begin{align*}
CE(y,\hat{y}) &= -\sum_iy_i\log(\hat{y}_i) \\ &=-\log(\hat{y}_o)
\end{align*}
\begin{align*}
\frac{\partial }{\partial v_c} CE(y,\hat{y}) &= -\frac{\partial }{\partial v_c} \log(y_o) \\
&= -\frac{1}{y_o} \frac{\partial }{\partial v_c} \frac{\exp(u_o^Tv_c)}{\sum_{w=1}^{V}\exp(u_w^Tv_c)} \\
&= -\frac{1}{y_o} \frac{1}{(\sum_{w=1}^{V}\exp(u_w^Tv_c))^2} ((\sum_{w=1}^{V}\exp(u_w^Tv_c))\exp(u_o^Tv_c)u_o -\exp(u_o^Tv_c)\sum_{w=1}^V \exp(u_w^Tv_c)u_w) \\
&= -\frac{1}{y_o} \frac{\exp(u_o^Tv_c)}{(\sum_{w=1}^{V}\exp(u_w^Tv_c))^2} ((\sum_{w=1}^{V}\exp(u_w^Tv_c))u_o - \sum_{w=1}^V \exp(u_w^Tv_c)u_w) \\
&= - \frac{1}{\sum_{w=1}^{V}\exp(u_w^Tv_c)} ((\sum_{w=1}^{V}\exp(u_w^Tv_c))u_o - \sum_{w=1}^V \exp(u_w^Tv_c)u_w) \\
&= -(u_o - \frac{\sum_{w=1}^V \exp(u_w^Tv_c)u_w}{\sum_{w=1}^{V}\exp(u_w^Tv_c)}) \\
&= \frac{\sum_{w=1}^V \exp(u_w^Tv_c)u_w}{\sum_{w=1}^{V}\exp(u_w^Tv_c)} - u_o
\end{align*}
(b)(3分)
这一问跟2(b)更类似。
当$k = o$时,
\begin{align*}
\frac{\partial }{\partial u_k} CE(y,\hat{y}) &= -\frac{\partial }{\partial u_k} \log(y_o) \\
&= -\frac{1}{y_o} \frac{\partial }{\partial u_k} \frac{\exp(u_o^Tv_c)}{\sum_{w=1}^{V}\exp(u_w^Tv_c)} \\
&= -\frac{1}{y_o} \frac{1}{(\sum_{w=1}^{V}\exp(u_w^Tv_c))^2} ((\sum_{w=1}^{V}\exp(u_w^Tv_c))\exp(u_o^Tv_c)v_c - \exp(u_o^Tv_c)\exp(u_k^Tv_c)v_c) \\
&= -\frac{1}{\sum_{w=1}^{V}\exp(u_w^Tv_c)} ((\sum_{w=1}^{V}\exp(u_w^Tv_c))v_c - \exp(u_k^Tv_c)v_c) \\
&= -(v_c - \hat{y}_k v_c) \\
&= (\hat{y}_k - 1)v_c
\end{align*}
当$k \neq o$时,
\begin{align*}
\frac{\partial }{\partial u_k} CE(y,\hat{y}) &= -\frac{\partial }{\partial u_k} \log(y_o) \\
&= -\frac{1}{y_o} \frac{\partial }{\partial u_k} \frac{\exp(u_o^Tv_c)}{\sum_{w=1}^{V}\exp(u_w^Tv_c)} \\
&= -\frac{1}{y_o} \frac{1}{(\sum_{w=1}^{V}\exp(u_w^Tv_c))^2} (0 - \exp(u_o^Tv_c)\exp(u_k^Tv_c)v_c) \\
&= -\frac{1}{\sum_{w=1}^{V}\exp(u_w^Tv_c)} (- \exp(u_k^Tv_c)v_c) \\
&= \hat{y}_kv_c
\end{align*}
将两种情况合并起来,
\begin{align*}
\frac{\partial }{\partial u_k} CE(y,\hat{y}) = (\hat{y}_k - y_k)v_c
\end{align*}
(c) (3分)
用negative sampling损失函数改写3(b):
\begin{align*}
\frac{\partial }{\partial u_o} J_{neg-sample} &= -\frac{\partial }{\partial u_o} \log(\sigma(u_o^Tv_c)) \\
&= -\frac{1}{\sigma(u_o^Tv_c)} \frac{\partial }{\partial u_o} \sigma(u_o^Tv_c) \\
&= -\frac{1}{\sigma(u_o^Tv_c)} \sigma(u_o^Tv_c)(1-\sigma(u_o^Tv_c))v_c \\
&= (\sigma(u_o^Tv_c)-1)v_c
\end{align*}
\begin{align*}
\frac{\partial }{\partial u_k} J_{neg-sample} &= -\frac{\partial }{\partial u_k} \sum_{i=1}^{K}\log(\sigma(-u_i^Tv_c)) \\
&= -\frac{\partial }{\partial u_k} \log(\sigma(-u_k^Tv_c)) \\
&= -\frac{1}{\sigma(-u_k^Tv_c)} \frac{\partial }{\partial u_k} \sigma(-u_k^Tv_c) \\
&= (1 - \sigma(-u_k^Tv_c))v_c
\end{align*}
之前计算softmax损失函数时,需要计算整个词表的概率分布,时间复杂的是$O(V)$。而使用negative sampling损失,时间复杂度降为了$O(K)$。
用negative sampling损失函数改写3(a):
\begin{align*}
\frac{\partial }{\partial v_c} J_{neg-sample} &= -\frac{\partial }{\partial v_c}\{\log(\sigma(u_o^Tv_c)) + \sum_{i=1}^{K}\log(\sigma(-u_i^Tv_c))\} \\
&= (\sigma(u_o^Tv_c)-1)u_o + \sum_{i=1}^{K} (1 - \sigma(-u_i^Tv_c))u_i
\end{align*}
(d)(8分)
我只求一下Skip-Gram模型的导数吧,CBOW的不准备做了。
假设$u_{t+j}$是词$w_{t+j}$对应的输出词向量。
1、使用softmax损失函数,再根据3(a)、3(b)算得的结果:
\begin{align*}
\frac{\partial }{\partial v_c} J_{softmax}(w_{t-m \cdots t+m}) &= \frac{\partial }{\partial v_c} \sum_{-m \leq j \leq m, j \neq 0} F(w_{t+j}, v_c) \\
&= \sum_{-m \leq j \leq m, j \neq 0} (\frac{\sum_{w=1}^V \exp(u_w^Tv_c)u_w}{\sum_{w=1}^{V}\exp(u_w^Tv_c)} - u_{t+j}) \\
\end{align*}
\begin{align*}
\frac{\partial }{\partial u_{t+j}} CE(y,\hat{y}) = (\hat{y}_{t+j} - y_{t+j})v_c
\end{align*}
2、并使用negative sampling损失函数,再根据3(c)算得的结果:
\begin{align*}
\frac{\partial }{\partial v_c} J_{skip-gram}(w_{t-m \cdots t+m}) &= \frac{\partial }{\partial v_c} \sum_{-m \leq j \leq m, j \neq 0} F(w_{t+j}, v_c) \\
&= \frac{\partial }{\partial v_c} \sum_{-m \leq j \leq m, j \neq 0} \{ -\log(\sigma(u_{t+j}^T)v_c) - \sum_{i=1}^{K_{j}} \log(\sigma(-u_{ji}^Tv_c))\} \\
&= \sum_{-m \leq j \leq m, j \neq 0} \{ (\sigma(u_{t+j}^Tv_c)-1)u_{t+j} + \sum_{i=1}^{K_{j}} (1 - \sigma(-u_{ji}^Tv_c))u_{ji} \}
\end{align*}
其中,$u_{ji}$是为词$w_{t+j}$负抽样出的第$i$个负样本,$K_j$是词$w_{t+j}$负抽样的总词数。
$\frac{\partial }{\partial u_{t+j}} J_{skip-gram}(w_{t-m \cdots t+m})$、$\frac{\partial }{\partial u_{ji}} J_{skip-gram}(w_{t-m \cdots t+m})$与上题中,对3(b)的改写是一样的。
(e)(12分)
我实现了Skip-Gram模型,没有去实现CBOW。参考代码
(f)(4分)
(g)(4分)
该题不需要写额外的代码,下载数据之后,运行q3 run.py即可训练词向量,最后生成如下的可视化图像:

4 情感分析(20分)
a(2分)
b(1分)
对机器学习任务引入正则项,是为了防止过拟合。如果不用正则项,会导致在训练集上面效果很好,模型自由度过高,充分拟合了训练集数据(包括噪声)。却无法一般化,推广到测试集,导致测试集效果很差。
c(2分)
虽然题目乍一看有点复杂,不过从分值就可以看出,该题的解答代码很简单。参考代码
d(3分)
预训练的GloVe在测试集达到了 37.96%的正确率(正则项系数$10^3$),而使用我自己训练的词向量正确率只有29.86%。我想这是因为:
1、GloVe的训练语料(Wikipedia data)要大得多
2、我的模型训练时,基本又有进行参数的调优。比如,词向量维度只有10,而GloVe词向量的维度至少是50
3、GloVe模型本身就要优于word2vec
e(4分)
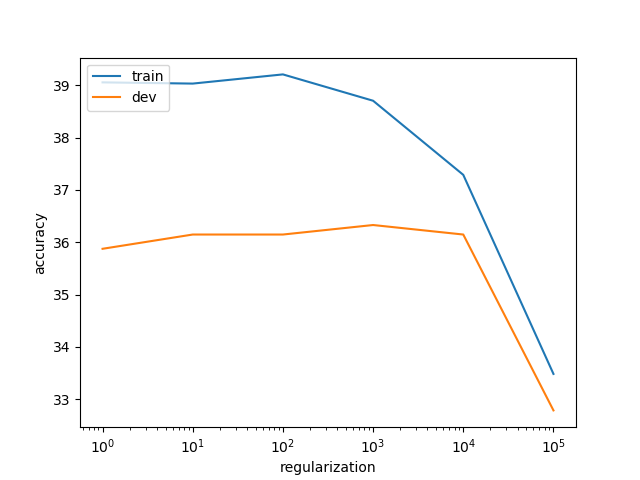
从图中可以看出,随着正则项系数的增大,训练集的正确率总体上是震荡下降的。而开发集(dev)有一个先缓慢上升然后下降的过程,并在$10^{3}$附近达到最大。
f(4分)

从图中可以看出,“-”预测为“+”、“+”预测为“-”这种严重的错误还是挺多的。甚至有两个“--”被预测为“++”的案例。
g(4分)
先来看两个“--”被预测为“++”的案例:
- “dull , lifeless , and amateurishly assembled .”这基本都是负面词汇,这不知道为什么预测得这么离谱。难道是标点符号所占比例太大导致的?
- “a lackluster , unessential sequel to the classic disney adaptation of j.m. barrie 's peter pan .”这句话出错情有可原吧,毕竟逻辑回归没那么智能。人类一眼就能看出,关键词是前两个形容词lackluster和unessential,及其负面。但无奈的是,后面跟真实情感无关的一些词比较正面,比如classic。
然后是“+”被预测为“--”的案例:
“chilling but uncommercial look into the mind of jeffrey dahmer , serial killer” 转折之后是重点,可以逻辑回归算法不知道这个常识。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号