神经网络及其训练
在前面的博客人工神经网络入门和训练深度神经网络,也介绍了与本文类似的内容。前面的两篇博客侧重的是如何使用TensorFlow实现,而本文侧重相关数学公式及其推导。
1 神经网络基础
1.1 单个神经元
一个神经元就是一个计算单元,传入$n$个输入,产生一个输出,再应用于激活函数。记$n$维输入向量为$x$,$n$维权重矩阵向量是$w$,偏置项为$b$,激活函数为sigmoid,最终激活后的输出为$a$:
\begin{align*}
a = \frac{1}{1 + \exp(-(w^T x + b))}
\end{align*}
将权重和偏置项组合在一起,得到如下公式:
\begin{align*}
a = \frac{1}{1 + \exp(-[w^T \quad b] \cdot [x \quad 1])}
\end{align*}
图1更直观地描述了该公式:
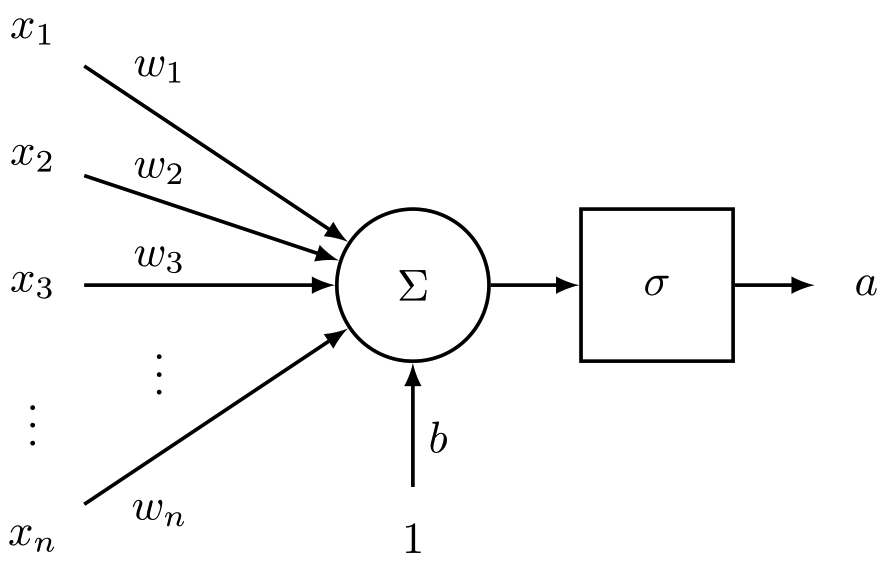
图1 单个神经元的输入及输出
1.2 单层神经元
将单个神经元扩展到一层,共$m$个神经元,每个神经元的输入都是$x$,权重记做$\{ w^{(i)}, \cdots, w^{(m)} \}$,偏置项记做$\{ b^{(i)}, \cdots, b^{(m)} \}$,则每个神经元激活后的输出:
\begin{align*}
a_1 &= \frac{1}{1 + \exp(-((w^{(1)})^T x + b_1))} \\
&\vdots \\
a_m &= \frac{1}{1 + \exp(-((w^{(m)})^T x + b_m))}
\end{align*}
下面我们定义更抽象的形式,以便用于复杂的神经网络:
\begin{align*}
&W = \begin{bmatrix} - & w^{(1)T} & -\\ & \cdots & \\ - & w^{(m)T} & - \end{bmatrix} \in \mathbb{R}^{m \times n} \\
&b = \begin{bmatrix} b_1\\ \vdots \\ b_m \end{bmatrix} \in \mathbb{R}^m \\
&z = Wx + b \\
&\sigma(z) = \begin{bmatrix} \frac{1}{1 + \exp(-z_1)}\\ \vdots \\ \frac{1}{1 + \exp(-z_m)} \end{bmatrix} \\
&\begin{bmatrix} a^{(1)}\\ \vdots \\ a^{(m)} \end{bmatrix} = \sigma(z) = \sigma(Wx + b)
\end{align*}
1.3 前馈计算

图2 简单的前馈神经网络
如图2所示的神经网络,只有1个隐层,输出:
\begin{align*}
s = U^T a = U^T f(Wx + b)
\end{align*}
其中,$f$是激活函数。
维度分析:假设词向量维度为2,一次使用5个词作为输入,则输入$x \in \mathbb{R}^{20}$。如果隐层有8个sigmoid神经元,并在输出层产生1个未规范化的分值,那么$W \in \mathbb{R}^{8 \times 20},b \in \mathbb{R}^{8},U \in \mathbb{R}^{8 \times 1},s \in \mathbb{R}$。
1.4 最大间隔目标函数
最大间隔目标函数的思想是,确保正样本的分值高于负样本的分值。这与SVM的目标韩式较为相似。正样本经神经网络计算,得到的分值记做$s$,负样本记做$s_c$,目标函数就是最大化$(s - s_c)$,或者最小化$(s_c - s)$。只有在$s_c > s$时才需要更新神经网络的参数。因此,如果$s_c > s$,则损失是$s_c - s$;否则,损失是0。因此损失函数:
\begin{align*}
J = \max(s_c-s,0)
\end{align*}
训练神经网络的目标是使得$J$最小。
为了得到一个更安全的边界,我们希望正样本分值比负样本分值大出$\Delta$(大于0),因此:
\begin{align*}
J = \max(s_c - s + \Delta ,0)
\end{align*}
其实为了简化公式,可以直接取$\Delta = 1$(根据SVM提到的知识,对函数距离的缩放,不会影响最终结果。$s$和$s_c$都是函数距离),模型在训练过程中其参数会自动适应这一约束,且不影响最终结果。此时目标函数:
\begin{align*}
J = \max(s_c - s + 1 ,0)
\end{align*}
1.5 反向传播训练模型
我们需要求得损失函数关于每个参数的偏导数,然后使用梯度下降更新参数:
\begin{align*}
\theta^{(t+1)} = \theta^{(t)} - \alpha \nabla_{\theta^{(t)}} J
\end{align*}
反向传播使用链式求导法则,求得损失函数关于每个参数的偏导数。为了进一步理解这一技术,首先看一下图3的神经网络:
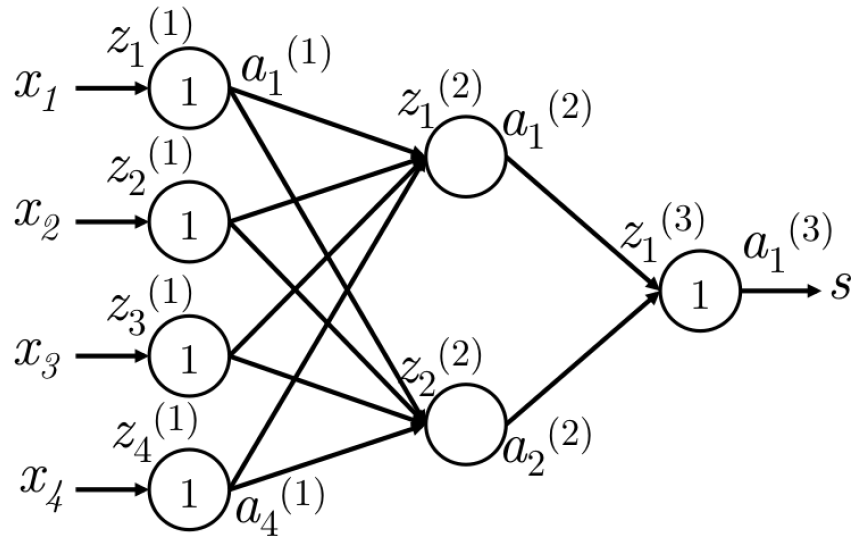
图3
上图的神经网络只有一个隐层,一个输出。为简单起见,定义以下概率:
- $x_i$是神经网络的一个输入
- $s$是神经网络的输出
- 第$k$层的第$j$个神经元接受标量输入$z^{(k)}_j$并产生标量激活输出$a^{(k)}_j$
- 将$z^{(k)}_j$算出的反向传播误差记做$\delta^{(k)}_j$
- 第一层是指输入层,而不是第一个隐层。对于输入层,$x_j = z^{(1)}_j = a^{(1)}_j$
- $W^{(k)}$是转移矩阵,将第$k$层的输出映射为第$k+1$层的输入
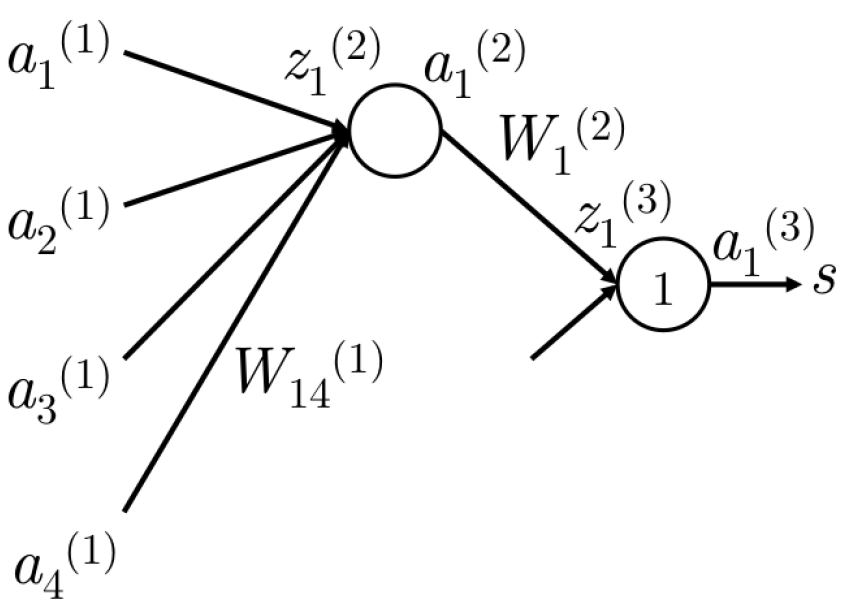
图4 与更新$W^{(1)}_{14}$相关的部分
如图4,如果要更新$W^{(1)}_{14}$,首先要意识到,只有在计算$z^{(2)}_1$时才会用到$W^{(1)}_{14}$。$z^{(2)}_1$仅仅用于计算了$a^{(2)}_1$,$a^{(2)}_1$与$W^{(2)}_1$用于计算最终的分值。首先有算是函数关于$s$和$s_c$的偏导数:
\begin{align*}
\frac{\partial J}{\partial s} = -\frac{\partial J}{\partial s_c} = -1
\end{align*}
为简单起见,我们只计算$\frac{\partial s}{\partial w^{(1)}_{ij}}$:
\begin{align*}
\frac{\partial s}{\partial w^{(1)}_{ij}} &= \frac{\partial W^{(2)} a^{(2)}}{\partial w^{(1)}_{ij}} \tag{1} \\
&= \frac{\partial W^{(2)}_i a^{(2)}_i}{\partial w^{(1)}_{ij}} \tag{2} \\
&= W^{(2)}_i \frac{\partial a^{(2)}_i}{\partial w^{(1)}_{ij}} \tag{3} \\
\end{align*}
第(1)步很直观,因为$s = W^{(2)} a^{(2)}$。第(2)步是因为,只有在计算标量$a^{(2)}_i$时,才会用到向量$W^{(1)}_i$。第(3)步也很直观,我们是在求关于$W^{(1)}_i$的偏导数,$W^{(2)}_i$直接看做常数。
然后应用链式法则:
\begin{align*}
W^{(2)}_i \frac{\partial a^{(2)}_i}{\partial w^{(1)}_{ij}} &= W^{(2)}_i \frac{\partial a^{(2)}_i}{\partial z^{(2)}_i} \frac{\partial z^{(2)}_i}{\partial w^{(1)}_{ij}} \\
&= W^{(2)}_i \frac{\partial f(z^{(2)}_i)}{\partial z^{(2)}_i} \frac{\partial z^{(2)}_i}{\partial w^{(1)}_{ij}} \\
&= W^{(2)}_i f'(z^{(2)}_i) \frac{\partial z^{(2)}_i}{\partial w^{(1)}_{ij}} \\
&= W^{(2)}_i f'(z^{(2)}_i) \frac{\partial}{\partial w^{(1)}_{ij}} (b^{(1)}_i + a^{(1)}_1W^{(1)}_{i1} + a^{(1)}_2W^{(1)}_{i2} + a^{(1)}_3W^{(1)}_{i3} + a^{(1)}_4W^{(1)}_{i4}) \\
&= W^{(2)}_i f'(z^{(2)}_i) a^{(1)}_j \\
&= \delta^{(2)}_i \cdot a^{(1)}_j
\end{align*}
$\delta^{(2)}_i$本质上是第2层第$i$个神经元反向传回的误差。
现在我们换一种方式,用误差分配和反向传播来讨论如何更新图4中的更新$W^{(1)}_{14}$:
- 首先从$a^{(3)}_1$反向传回误差1
- 这个误差乘以把$z^{(3)}_1$映射到$a^{(3)}_1$的神经元的导数。由于输出层没有激活函数,$z^{(3)}_1 = a^{(3)}_1$,因此这一导数刚好是1,乘积依然是1,也就是$\delta^{(3)}_1 = 1$
- 目前误差已经反向传播到了$z^{(3)}_1 = 1$,我们需要将误差“公平分配”给$a^{(2)}_1 = 1$
- 到达$a^{(2)}_1$的误差是$\delta^{(3)}_1 \times W^{(2)}_1 = W^{(2)}_1$
- 和第2不一样,求得将$z^{(2)}_1$映射到a^{(2)}_1$的神经元的导数$f'(z^{(2)}_1)$
- 到达$z^{(2)}_1$的误差$f'(z^{(2)}_1)W^{(2)}_1$,也就是$\delta^{(2)}_1 = 1$
- 然后需要将误差“公平分配”给$W^{(1)}_{14}$,也就是上一步的误差乘以$a^{(4)}_1$
- 因此,最终得到损失函数关于$W^{(1)}_{14}$的偏导数$a^{(4)}_1 f'(z^{(2)}_1) W^{(2)}_{1}$
以上我们用链式法则和误差分配反向传播得到的结果是一样的。
偏置项更新:偏置项也可以看成输入向量的一个维度,只不过这个维度始终为1(这种1.1小节中的第二个公式就可以看出)。因此,第$k$层第$i$个神经元偏置项的偏导数直接就是$\delta^{(k)}_i$。例如,在上面我们是要更新$b^{(1)}_1$,而不是$W^{(1)}_{14}$,那么梯度直接就是$f'(z^{(2)}_1) W^{(2)}_{1}$。
将$\delta^{(k)}$到$\delta^{(k-1)}$的误差计算一般化:
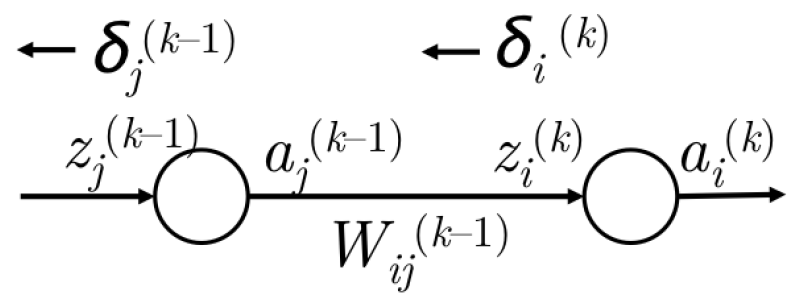
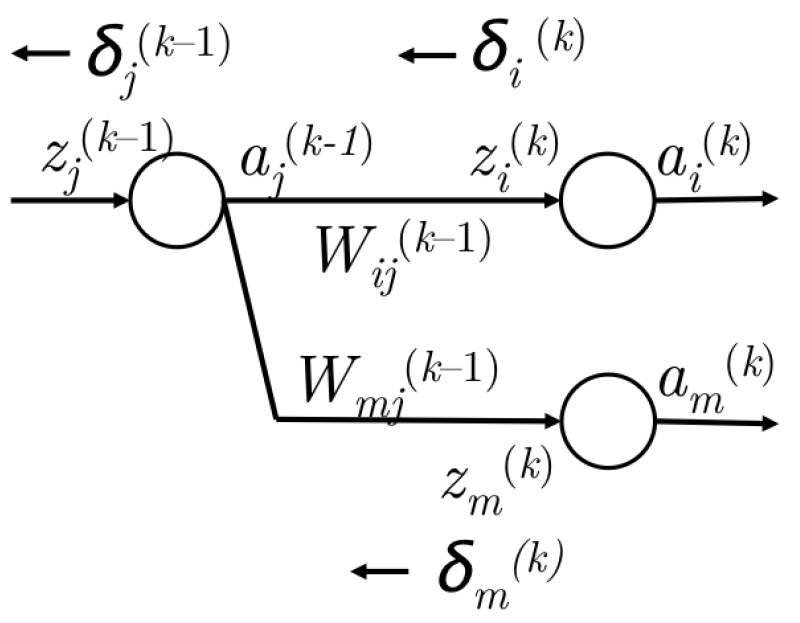
图5 从$\delta^{(k)}$到$\delta^{(k-1)}$的误差传播
- 我们已经有了从$z^{(k)}_i$传回的误差$\delta^{(k)}$,如图5左侧所示
- 计算反向传给$a^{(k-1)}_j$的误差,通过$\delta^{(k)}_i$乘以路径权重$W^{(k-1)}_{ij}$
- 因此,$a^{(k-1)}_j$接收到的误差就是$\delta^{(k)}_i W^{(k-1)}_{ij}$
- 然而,$a^{(k-1)}_j$可能会前馈到下一层的多个节点,如图5右侧所示。这样的话,$a^{(k-1)}_j$还要接收从$k$层的节点$m$反向传回的误差。
- 一次,$a^{(k-1)}_j$接收到的误差是$\delta^{(k)}_i W^{(k-1)}_{ij} + \delta^{(k)}_m W^{(k-1)}_{mj}$
- 事实上,这可以一般化为$\sum_i \delta^{(k)}_i W^{(k-1)}_{ij}$
- 现在已经有了$a^{(k-1)}_j$的误差,并且$a^{(k-1)}_j$关于$z^{(k-1)}_j$的导数为$f'(z^{(k-1)}_j)$
- 因此,误差传到了$z^{(k-1)}_j$,记做$\delta^{(k-1)}_j$,大小为$f'(z^{(k-1)}_j) \sum_i \delta^{(k)}_i W^{(k-1)}_{ij}$
1.6 反向传播训练向量化
用向量化的代码取代for循环,有助于提高代码的执行效率(可以充分利用GPU加速吧?)。
上面我们给出了如何计算一个参数的梯度,现在我们介绍更一般化的方法,一次性地更新整个权重矩阵和偏置向量。这一简单的扩张有助于为我们建立一种直觉,误差传播可以抽象到矩阵-向量级别。
给出一个权重$W^{(k)}_{ij}$,我们定义其误差梯度为$\delta^{(k+1)}_i \cdot a^{(k)}_j$。$W^{(k)}$是将$a^{(k)}$映射为$z^{(k+1)}$的权重矩阵。我们可以建立整个矩阵$W^{(k)}$的误差梯度:
\begin{align*}
\nabla_{W^{(k)}} = \begin{bmatrix}
\delta^{(k+1)}_1 a^{(k)}_1 & \delta^{(k+1)}_1 a^{(k)}_2 &\cdots \\
\delta^{(k+1)}_2 a^{(k)}_1 & \delta^{(k+1)}_2 a^{(k)}_2 &\cdots \\
\vdots & \vdots & \ddots
\end{bmatrix}
= \delta^{(k+1)} a^{(k)T}
\end{align*}
下面我们来看如何计算误差向量$\delta^{(k)}$。在图5中我们已经知道,$\delta^{(k)}_j = f'(z^{(k)}_j) \sum_i \delta^{(k+1)}_i W^{(k)}_{ij}$,这可以一般化为如下的矩阵形式:
\begin{align*}
\delta^{(k)} = f'(z^{(k)}) \circ (W^{(k)T}\delta^{(k+1)}_i)
\end{align*}
其中,$\circ$运算符是指矩阵点乘($\mathbb{R}^N \circ \mathbb{R}^N \rightarrow \mathbb{R}^N$)。
计算效率:我们探索了基于元素的更新和基于矩阵的更新。我们必须意识到,向量化的实现在科学运算环境里效率更高,比如MATLAB和Python的NumPy/SciPy包。因此,我们应该使用向量化的实现。更进一步,在反向传播时应该避免重复计算。比如,$\delta^{(k)}$直接依赖于$\delta^{(k+1)}$。我们应该确保,在使用$\delta^{(k+1)}$更新完$W^{(k)}$之后,不能丢弃,而是要保存训练,用于后面计算$\delta^{(k)}$。重复这一过程$(k-1) \cdots (1)$。最终得到了一个计算上还负担得起的递归过程。
本文翻译自CS224n课程的官方笔记3,对应该课程的第4、5节。笔记的后半部分还介绍了神经网络的一些实践经验以及技巧,这与先前的博客训练深度神经网络存在较大重叠,所以并没有写在这里。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号