转 :原码,反码,补码
数值在计算机中是以补码的方式存储的,在探求为何计算机要使用补码之前, 让我们先了解原码, 反码和补码的概念。
对于一个数, 计算机要使用一定的编码方式进行存储。 原码, 反码, 补码是计算机存储一个具体数字的编码方式。
一个数在计算机中的二进制表示形式, 叫做这个数的机器数。机器数是带符号的,在计算机用一个数的最高位存放符号, 正数为0, 负数为1。比如,十进制中的数 +2 ,计算机字长为8位,转换成二进制就是[00000010]。如果是 -2 ,就是 [10000010] 。因为第一位是符号位,所以机器数的形式值就不等于真正的数值。例如上面的有符号数 [10000010],其最高位1代表负,其真正数值是 -2 而不是形式值130([10000010]转换成十进制等于130)。所以将带符号位的机器数对应的真正数值称为机器数的真值。
- 原码就是符号位加上真值的绝对值, 即用第一位表示符号, 其余位表示值。
- 反码的表示方法是:正数的反码是其本身;负数的反码是在其原码的基础上, 符号位不变,其余各个位取反。
- 补码的表示方法是:正数的补码就是其本身;负数的补码是在其原码的基础上, 符号位不变, 其余各位取反, 最后+1。 (即在反码的基础上+1)
举例:
| 十进制数 | 原码 | 反码 | 补码 |
|---|---|---|---|
| 85 | 0101 0101 |
0101 0101 |
0101 0101 |
| -85 | 1101 0101 |
1010 1010 |
1010 1011 |
| 9 | 0000 1001 |
0000 1001 |
0000 1001 |
| -9 | 1000 1001 |
1111 0110 |
1111 0111 |
那么计算机为什么要使用补码呢?
首先,根据运算法则减去一个正数等于加上一个负数, 即: 1-1 = 1+(-1), 所以计算机被设计成只有加法而没有减法, 而让计算机辨别”符号位”会让计算机的基础电路设计变得十分复杂,于是就让符号位也参与运算,从而产生了反码。
用反码计算, 出现了”0”这个特殊的数值, 0带符号是没有任何意义的。 而且会有[0000 0000]和[1000 0000]两个编码表示0。于是设计了补码, 负数的补码就是反码+1,正数的补码就是正数本身,从而解决了0的符号以及两个编码的问题: 用[0000 0000]表示0,用[1000 0000]表示-128。
注意-128实际上是使用以前的-0的补码来表示的, 所以-128并没有原码和反码。使用补码, 不仅仅修复了0的符号以及存在两个编码的问题, 而且还能够多表示一个最低数。 这就是为什么8位二进制, 使用补码表示的范围为[-128, 127]。
-----------------------------------------------------------------------------------------------------------------------------------------------
1.使用补码,可以将符号位和其它位统一处理;同时,减法也可按加法来处理。
2.使用补码, 不仅仅修复了0的符号以及存在两个编码的问题, 而且还能够多表示一个最低数. 这就是为什么8位二进制, 使用原码或反码表示的范围为[-127, +127], 而使用补码表示的范围为[-128, 127].
(-1) + (-127) = [1000 0001]原 + [1111 1111]原 = [1111 1111]补 + [1000 0001]补 = [1000 0000]补
-1-127的结果应该是-128, 在用补码运算的结果中, [1000 0000]补 就是-128. 但是注意因为实际上是使用以前的-0的补码来表示-128, 所以-128并没有原码和反码表示.(对-128的补码表示[1000 0000]补算出来的原码是[0000 0000]原, 这是不正确的)
四.补码表示的溢出问题
以下是本人的补充的理解,不知道是否正确:
由于计算机中的数字用补码表示,例如8bit的byte类型的表示范围为:
[-128, 127]
0 = [0000 0000](补)
-128 = [1000 0000](补)
127 = [0111 1111](补)
当byte类型的变量超上限127时,如:
+128 = -(-128)= 127 + 1
= [1111 1111](补)+ [0000 0001](补)
= [1000 0000](补)
= -128
+129 = 127 + 2
= [1111 1111](补)+ [0000 0001](补)
= [1000 0001](补)
= [1111 1111](原)
= -127
当byte类型的变量超过下限-128时:
-129 = -128 - 1
= [1000 0000](补) - [0000 0001](补)
= [0111 1111](补)
= 127
-130 = -128 - 2
= [1000 0000](补) - [0000 0010](补)
= [0111 1110](补)
= 126
byte a = -128, b = (byte) 128, c = (byte) 129, d = (byte) 130;
byte e = (byte) -129, f = (byte) -130;
System.out.println(a == ((byte)-a)); // true
System.out.println(b); // -128
System.out.println(c); // -127
System.out.println(d); // -126
System.out.println(e); // 127
System.out.println(f); // 126
五.原码, 反码, 补码 再深入(不一定要搞懂)
计算机巧妙地把符号位参与运算, 并且将减法变成了加法, 背后蕴含了怎样的数学原理呢?
将钟表想象成是一个1位的12进制数. 如果当前时间是6点, 我希望将时间设置成4点, 需要怎么做呢?我们可以:
1. 往回拨2个小时: 6 - 2 = 4
2. 往前拨10个小时: (6 + 10) mod 12 = 4
3. 往前拨10+12=22个小时: (6+22) mod 12 =4
2,3方法中的mod是指取模操作, 16 mod 12 =4 即用16除以12后的余数是4.
所以钟表往回拨(减法)的结果可以用往前拨(加法)替代!
现在的焦点就落在了如何用一个正数, 来替代一个负数. 上面的例子我们能感觉出来一些端倪, 发现一些规律. 但是数学是严谨的. 不能靠感觉.
首先介绍一个数学中相关的概念: 同余
同余的概念
两个整数a,b,若它们除以整数m所得的余数相等,则称a,b对于模m同余
记作 a ≡ b (mod m)
读作 a 与 b 关于模 m 同余。
举例说明:
4 mod 12 = 4
16 mod 12 = 4
28 mod 12 = 4
所以4, 16, 28关于模 12 同余.
负数取模
正数进行mod运算是很简单的. 但是负数呢?
下面是关于mod运算的数学定义:
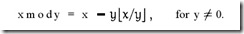
上面是截图, "取下界"符号找不到如何输入(word中粘贴过来后乱码). 下面是使用"L"和"J"替换上图的"取下界"符号:
x mod y = x - y L x / y J
上面公式的意思是:
x mod y等于 x 减去 y 乘上 x与y的商的下界.
以 -3 mod 2 举例:
-3 mod 2
= -3 - 2xL -3/2 J
= -3 - 2xL-1.5J
= -3 - 2x(-2)
= -3 + 4 = 1
所以:
(-2) mod 12 = 12-2=10
(-4) mod 12 = 12-4 = 8
(-5) mod 12 = 12 - 5 = 7
开始证明
再回到时钟的问题上:
回拨2小时 = 前拨10小时
回拨4小时 = 前拨8小时
回拨5小时= 前拨7小时
注意, 这里发现的规律!
结合上面学到的同余的概念.实际上:
(-2) mod 12 = 10
10 mod 12 = 10
-2与10是同余的.
(-4) mod 12 = 8
8 mod 12 = 8
-4与8是同余的.
距离成功越来越近了. 要实现用正数替代负数, 只需要运用同余数的两个定理:
反身性:
a ≡ a (mod m)
这个定理是很显而易见的.
线性运算定理:
如果a ≡ b (mod m),c ≡ d (mod m) 那么:
(1)a ± c ≡ b ± d (mod m)
(2)a * c ≡ b * d (mod m)
如果想看这个定理的证明, 请看:http://baike.baidu.com/view/79282.htm
所以:
7 ≡ 7 (mod 12)
(-2) ≡ 10 (mod 12)
7 -2 ≡ 7 + 10 (mod 12)
现在我们为一个负数, 找到了它的正数同余数. 但是并不是7-2 = 7+10, 而是 7 -2 ≡ 7 + 10 (mod 12) , 即计算结果的余数相等.
接下来回到二进制的问题上, 看一下: 2-1=1的问题.
2-1=2+(-1) = [0000 0010]原 + [1000 0001]原= [0000 0010]反 + [1111 1110]反
先到这一步, -1的反码表示是1111 1110. 如果这里将[1111 1110]认为是原码, 则[1111 1110]原 = -126, 这里将符号位除去, 即认为是126.
发现有如下规律:
(-1) mod 127 = 126
126 mod 127 = 126
即:
(-1) ≡ 126 (mod 127)
2-1 ≡ 2+126 (mod 127)
2-1 与 2+126的余数结果是相同的! 而这个余数, 正式我们的期望的计算结果: 2-1=1
所以说一个数的反码, 实际上是这个数对于一个模的同余数. 而这个膜并不是我们的二进制, 而是所能表示的最大值! 这就和钟表一样, 转了一圈后总能找到在可表示范围内的一个正确的数值!
而2+126很显然相当于钟表转过了一轮, 而因为符号位是参与计算的, 正好和溢出的最高位形成正确的运算结果.
既然反码可以将减法变成加法, 那么为什么现在计算机使用的补码呢? 为什么在反码的基础上加1, 还能得到正确的结果?
2-1=2+(-1) = [0000 0010]原 + [1000 0001]原 = [0000 0010]补 + [1111 1111]补
如果把[1111 1111]当成原码, 去除符号位, 则:
(0111 1111]原 = 127
其实, 在反码的基础上+1, 只是相当于增加了模的值:
(-1) mod 128 = 127
127 mod 128 = 127
2-1 ≡ 2+127 (mod 128)
此时, 表盘相当于每128个刻度转一轮. 所以用补码表示的运算结果最小值和最大值应该是[-128, 128].
但是由于0的特殊情况, 没有办法表示128, 所以补码的取值范围是[-128, 127].




 浙公网安备 33010602011771号
浙公网安备 33010602011771号