leetcode 目标和 中等

 

 

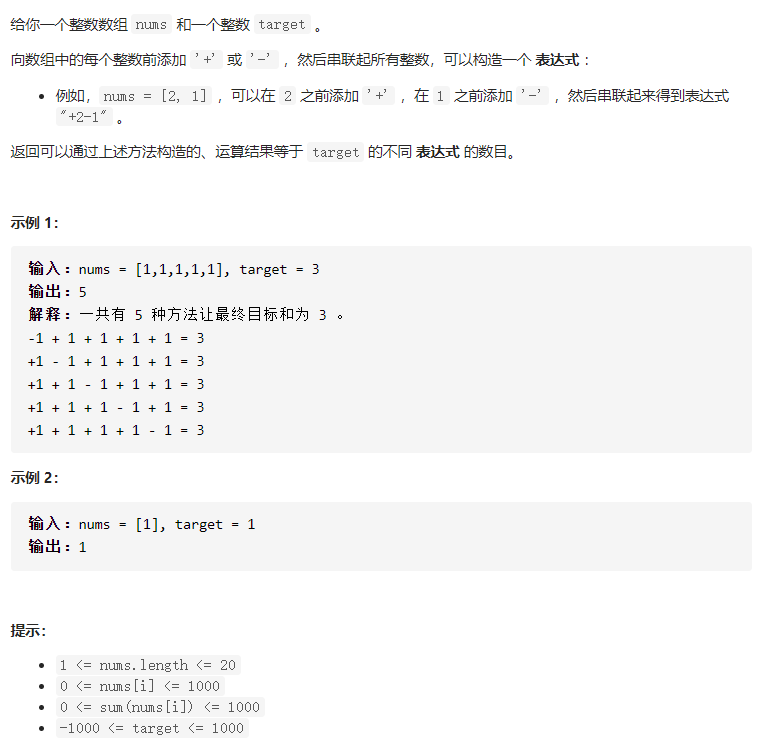
① 可以直接 dfs + 一些小的剪枝来做；

② dp[i][j] 表示前 i 个数都使用，和为 j 的方案数。由于和可能为负，但 sum(num[i]) 最大值为 1000，所以可以开 2000 大小的数组，并做一个偏移量来解决负数和问题；

③ 假设添加符号的数的和为 a，那么另一半数的和为 sum - a，即 (sum - a) + (-a) = target，有 a = (sum - target) / 2，最终变为求数组挑选一些数，使得其和为 a 的方案数。一样的可以用dp做

 

 

class Solution {
public:
    int findTargetSumWays(const vector<int>& nums, const int &target) {
        int sum = 0;
        for(auto &num : nums) sum += num;
        int tar = sum - target;
        if(tar < 0 || tar & 1) return 0;
        tar /= 2;
        vector<int> dp[2];
        dp[0].resize(tar + 1, 0);
        dp[1].resize(tar + 1, 0);
        for(int i = 0; i < nums.size(); ++ i) {
            if(i == 0) {
                dp[i][0] = 1;       // 不加 nums[i] 这个数
                if(nums[i] <= tar) {
                    ++ dp[i][nums[i]];  // 加 nums[i] 这个数, 由于 nums[i] 可能 == 0, 所以这里用 ++
                }
                continue;
            }
            for(int j = 0; j <= tar; ++ j) {
                dp[i % 2][j] = dp[(i - 1) % 2][j];     // 不加 nums[i]
                if(j >= nums[i]){
                    dp[i % 2][j] += dp[(i - 1) % 2][j - nums[i]];  // 加 nums[i]
                }
            }
        }
        return dp[(nums.size() - 1) % 2][tar];
    }
};

 

class Solution {
public:
    int findTargetSumWays(const vector<int>& nums, const int &target) {
        // dp[i][j] 前 i 个数, 和为 j 的方案数
        vector<vector<int>> dp(nums.size());
        for(auto &item : dp) item.resize(2100, 0);
        for(int i = 0; i < nums.size(); ++ i) {
            if(i == 0) {
                // 以 1050 作为偏移量
                // 注意: 两者不是连等赋值为 1, 因为当 nums[i] == 0 时, 初始化所得值应该为 2
                ++ dp[i][-nums[i] + 1050];
                ++ dp[i][nums[i] + 1050];
                continue;
            }
            for(int j = 0; j < 2100; ++ j) {
                if(j >= nums[i]) dp[i][j] += dp[i - 1][j - nums[i]];
                if(j + nums[i] < 2100) dp[i][j] += dp[i - 1][j + nums[i]];
            }
        }
        return dp.back()[target + 1050];
    }
};

 

class Solution {
public:
    int findTargetSumWays(const vector<int>& nums, const int &target) {
        if(nums.empty()) return 0;
        sumA.reserve(nums.size());
        for(int i = nums.size() - 1; i >= 0; -- i) {
            if(i == nums.size() - 1) {
                sumA[i] = nums[i];
                continue;
            }
            sumA[i] = sumA[i + 1] + nums[i];
        }
        solve(nums, target, 0, 0);
        return ans;
    }

private:
    int ans = 0;
    vector<int> sumA;
    void solve(const vector<int> &nums, const int &target, int sum, int l) {
        if(l == nums.size()) {
            if(target == sum) ++ ans;
            return ;
        }
        if(sum - sumA[l] > target || sum + sumA[l] < target) return ;
        solve(nums, target, sum + nums[l], l + 1);
        solve(nums, target, sum - nums[l], l + 1);
    }
};