剪邮票 --全排列和DFS

剪邮票

有12张连在一起的的12生肖邮票，现在你要从中剪下5张来，要求必须是连着的。（仅仅连接一个角不算相连）请你计算，一共有多少种不同的剪去方法。

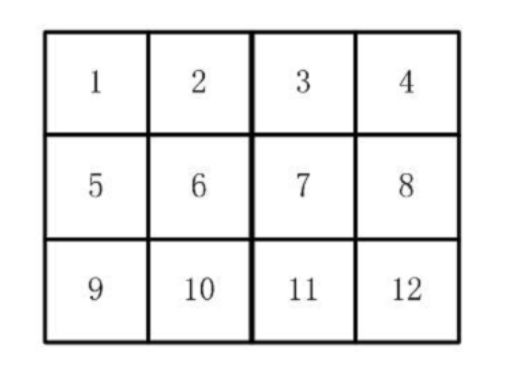
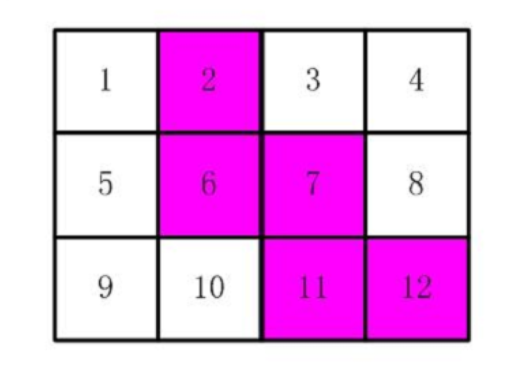
　　看到这个题一开始我直接认为DFS搜索12次就行了。

　　肯定没那么简单。因为有几种情况是搜索不到的，比如：

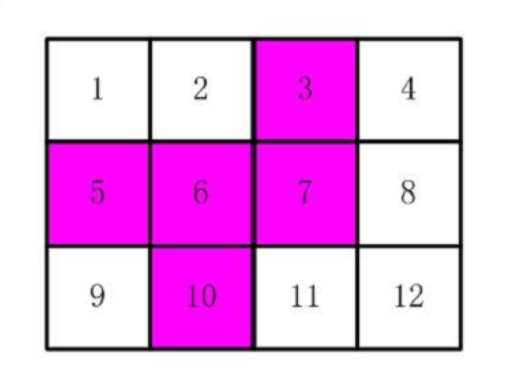
     可以转换成一个思路，就是随机找个5张邮票，看它们能不能凑成一张大邮票；

　　

#include <stdio.h>

int cnt = 0, ans = 0;
int a[5];//用来存放，组合数列
int next[4][2] = {{0,1},{1,0},{0,-1},{-1,0}};
int book[50][50];
int g[50][50];
void dfs(int x, int y){
    int i;
    cnt++;
    book[x][y] = 1;
    for(i = 0; i < 4; i++){
        int tx = x + next[i][0];
        int ty = y + next[i][1];
        if(tx >= 0 && tx < 3 && ty >= 0 && ty < 4 && book[tx][ty] == 0 && g[tx][ty] == 1){
            dfs(tx, ty);
        }
    }
}
void solve(int step, int k){
    int i;
    if(step == 5){
        int x, y;
        for(i = 0; i < 5; i++){
            x = (a[i] - 1) / 4;
            y = (a[i] - 1) % 4;
            g[x][y] = 1; 
        }

        dfs((a[0] - 1) / 4, (a[0] - 1) % 4);
        if(cnt == 5){
            ans++;
        }
        cnt = 0;
        memset(g,0,sizeof(g));
        memset(book,0,sizeof(book));
    }                                                  
    for(i = k + 1; i <= 12; i++){
        a[step] = i;
        solve(step + 1, i);
    }
}
int main() {
    int i, j;
    solve(0, 0); 
    printf("%d\n",ans);
    
    return 0;
}

 

注意问题：

　　以后在搜索地图的时候一定要把book[x][y]写在刚进函数时，而不是写在进函数前，否则初始点可能会被忘记记录，一定要养成习惯，在for循环里不多BB！

题目知识点：

　　（1）数的全排列，是每次的排列组合里面的数都是不完全一样的，例如 有 1 2 3 4 5 就不会再出现 1 2 3 5 4.

　　（2）一维数组转换成二维数组。