int变量与字符编码问题

数据类型

整型

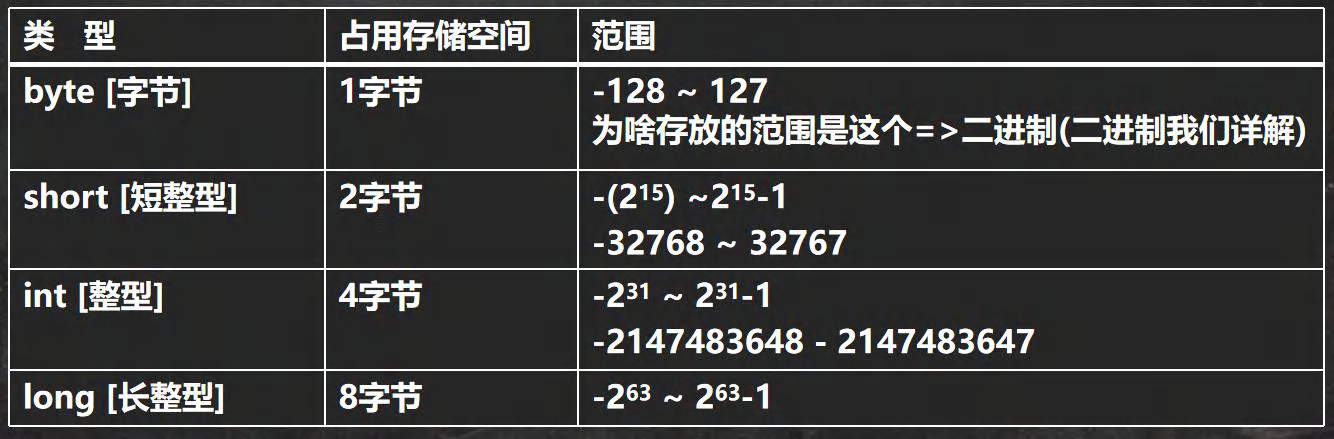
这里引入第一个问题：为什么byte的存放范围是-128~127呢？

首先补充计算机的基础知识：二进制

其实是因为硬件上的二极管的限制，一个1节是8个bit，这里的bit其实就是二极管

其实是根据二进制的规律，然后设计出反码来解决减法运算，设计出补码来解决0的符号问题
int 是4个字节，1个字节等于8个比特，共有4*8个比特，每个比特位不是1就是0，那么就有2种选择，
而在二进制里，我们把第一个比特位用来表示正负，0为正数，1为负数。我们把32个比特位都用上，再减去用来表示正负第一个比特位，有31个比特位可以用，也就是有231个组合方式，那么大家可能会自然想到，231就是最大值，但是，最重要的一点大家忽略了，

因为我们现实生活中一般是从1开始计数，我们自然就认为231就是最大值，
可我们计算机里是从0开始计数，组合数231要减去1才是int型能表示的最大值。

原码，反码，补码

基本规则

1、正数的原码、反码、补码都一样；
2、负数的反码 = 它的原码符号位不变，其他位取反（取反的意思：0 换成 1 、 1 换成 0 ）；
3、负数的补码 = 它的反码 +1；
4、0的反码、补码都是0；

思考1：为什么Java中byte的取值范围为-128~127？

（计算机的二进制问题）第一位表示的是符号位.而使用补码表示时又可以多保存一个最小值。因为首先byte是一个字节，即为8个比特，最高位是符号位，则能够表示数值的只有7个位置，对于正数而言：00000000~01111111(补码形式)，也就是十进制的0-127.对于负数而言：10000000-11111111，由于计算机中为了避免存在-0，因此将10000000定为-128，因此多保留了这个-128最小值，则byte的取值范围为-128—127。

思考2：为什么要有反码和补码

其实就是计算机中没有办法直接识别符号位

计算十进制的表达式: 1-1=0

　　1 - 1 = 1 + (-1) = [00000001]原 + [10000001]原 = [10000010]原 = -2

　　如果用原码表示, 让符号位也参与计算, 显然对于减法来说, 结果是不正确的.这也就是为何计算机内部不使用原码表示一个数.（符号位正常参与运算）

　　为了解决原码做减法的问题, 出现了反码:

　　计算十进制的表达式: 1-1=0

　　1 - 1 = 1 + (-1) = [0000 0001]原 + [1000 0001]原= [0000 0001]反 + [1111 1110]反 = [1111 1111]反 = [1000 0000]原 = -0
但是，对于绝大多数运算，将减法转化为补码就可以了，但是这里出现了一个问题：就是而且会有[0000 0000]原和[1000 0000]原两个编码表示0。

​ 为了解决0的符号问题，出现了补码：

​ 1-1 = 1 + (-1) = [0000 0001]原 + [1000 0001]原 =[0000 0001]反 + [1111 1110]反= [0000 0001]补 + [1111 1111]补 = [10000 0000]补=[0000 0000]原

​ 这样0用[0000 0000]表示, 而以前出现问题的-0则不存在了.而且可以用[1000 0000]表示-128:

​ 因此-128只有补码，没有反码与原码

思考3:移位操作

为什么负数不断地无符号移动的最小值是1？

以整型为例，因为移动的位数是一个MOD32的结果，当移动31位时，除了最右边为1，其他均为0，因此为1，当移动到32位时，则为原数值本身。

参考资料：

字节的数据解释

反码补码的比较

int变量的范围

字符的编码

utf-8（通用编码）

可变长编码方案：分为1个字节，2个字节，3个字节，4个字节

——这也是为何英文数据集乱码出现较少，中文数据集乱码较多的原因。