AT ARC192E Snuke's Kyoto Trip

本题需要用到一个结论：在一个 \(n\times m\)（边长）的矩形中，只往 \(x, y\) 正方向走，记 \(f(n, m)\) 为起点为 \((0, 0)\) 终点任选的路径数，\(g(n, m)\) 为起点终点均任选的路径数，则有 \(f(n, m) = \binom{n + m + 2}{n + 1} - 1, g(n, m) = \binom{n + m + 4}{n + 2} - (n + 2)(m + 2) - 1\)。
下面给出一个比较直观的证明（最后也有本题题解）。

首先考虑起点为 \((0, 0)\)，终点为 \((n, m)\)。
那就是有 \(n\) 步向 \(x\) 正方向，\(m\) 步向 \(y\) 正方向，所以路径数为 \(\binom{n + m}{n}\)。

接下来考虑起点为 \((0, 0)\)，终点为 \((n, i)(0\le i\le m)\)，也就是最后一列上的点，如图：

那么一个经典的想法是在最后一列的终点都往右拐再汇到 \(n + 1\) 列的同一个点，如图：

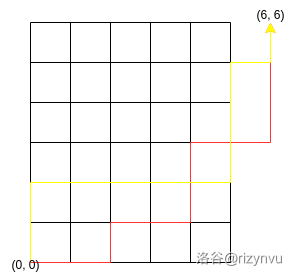
于是会发现所有路径都可以对应上一条 \((0, 0)\) 到 \((n + 1, m)\) 的路径，所以路径数即为 \(\binom{n + m + 1}{n + 1}\)。

然后来考虑 \(f(n, m)\)，即起点为 \((0, 0)\) 终点任选，如图：

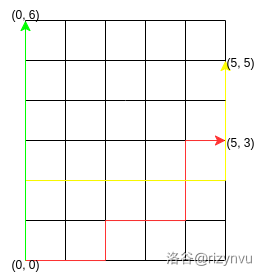
考虑类似上面对第 \(n\) 列的处理，对 \(0\sim n\) 的每一列做上面的变换。
此时到第 \(i\) 列的路径就全部可以转为到 \((i + 1, m)\) 的路径。
那么就变成了 \((0, 0)\) 到 \((i, m)(1\le i\le n + 1)\) 的路径数，即：

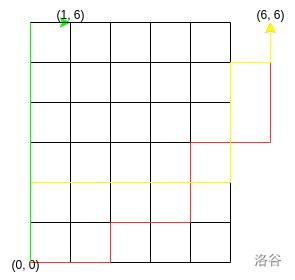
考虑手动补上一个 \((0, 0)\) 到 \((0, m)\) 的方案数 \(1\)，此时就成了所有 \((0, 0)\) 到 \((i, m)(0\le i\le n + 1)\) 的路径数。
发现这个时候的情况其实是与 \((0, 0)\) 到一列的情况一样的，因为这其实就是到一行，交换 \(x, y\) 就一样了。
所以再类似的做一次变换，如图：

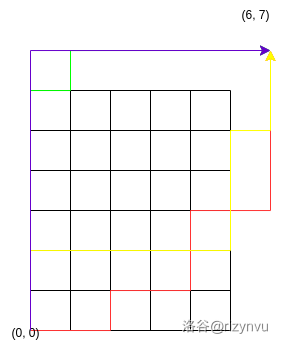
于是此时所有路径就对应到了 \((0, 0)\) 到 \((n + 1, m + 1)\) 的路径上。
而需要注意的是紫色这条是算不了的，因为这对应的是 \((0, 0)\) 到 \((0, m)\) 的路径。
所以有 \(f(n, m) = \binom{n + m + 2}{n + 1} - 1\)。

接下来考虑 \(g(n, m)\)，即起点终点都任选，如图：

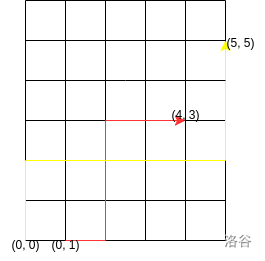
考虑对每个 \((i, j)(0\le i\le n, 0\le j\le m)\) 都作为起点算一次，用上面的推导能够知道这就是 \((i, j)\) 到 \((n + 1, m + 1)\) 的路径数 \(-1\)。
此时先抛去这个 \(-1\)，最后 \(-(n + 1)(m + 1)\) 即可。
那需要求的就是所有 \((i, j)\) 到 \((n + 1, m + 1)\) 的路径数。
把起点终点倒过来，那就是 \((n + 1, m + 1)\) 到所有 \((i, j)(0\le i\le n, 0\le j\le m)\) 的路径数，如图：

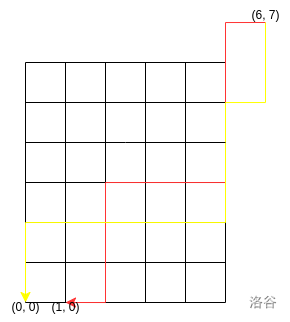
类似的考虑补齐这个图，如果也加上 \((n + 1, m + 1)\) 到 \((n + 1, m + 1), (i, m + 1)(0\le i\le n), (n + 1, j)(0\le j\le m)\) 的路径，要求的就变成了 \((n + 1, m + 1)\) 到 \((i, j)(0\le i\le n + 1, 0\le j\le m + 1)\) 的路径数。
那这不就是起点从左下角变成了右上角吗，所以又可以对应到 \((n + 1, m + 1)\) 到 \((-1, -1)\) 的路径，如图：

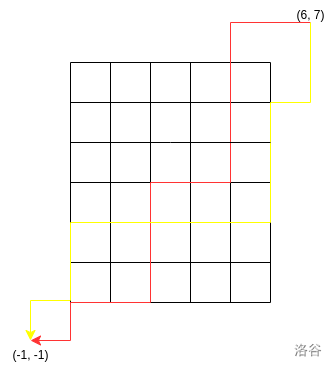
于是有 \(g(n, m) = f(n + 2, m + 2) - (n + 1)(m + 1) - 1 - (n + 1) - (m + 1)\)，其中 \(-1 - (n + 1) - (m + 1)\) 是为了减去补全的路径数。
写好看点就是 \(g(n, m) = \binom{n + m + 4}{n + 2} - (n + 1)(m + 1) - (n + 1) - (m + 1) - 2 = \binom{n + m + 4}{n + 2} - (n + 2)(m + 2) - 1\)。

---

以下是题解。

首先题目就是要求路径不能过 \((x, y)(L\le x\le R, D\le y\le U)\)。

那考虑容斥，先求出没有限制的方案数：\(g(n, m)\)。

然后考虑减掉经过了这个矩形的方案数。
因为只能往 \(x, y\) 正方向走，于是要走进这个矩形一定是从左边或下边进入，要走出这个矩形一定是从右边或者上边出去，于是分类讨论：

• 起点终点都在矩形内，那就是 \(g(R - L, U - D)\)。

• 路径过程中进入了这个矩形。
  那么一定会有一步是向右走到矩形的左边界或向上走到矩形的下边界。

  所以可以枚举左边界和下边界的点，\(\mathcal{O}(1)\) 算出起点到该点与该点到终点的方案数相乘。
  因为点数是 \(\mathcal{O}(H + W)\)，所以是可接受的。

• 路径起点在矩形内，终点不在矩形内。
  那类似上面一种情况，肯定会从上边界向上走出去或者右边界向右走出去。

  一样的枚举边界上的点 \(\mathcal{O}(1)\) 计算贡献。

于是最后的时间复杂度为 \(\mathcal{O}(H + W)\)。

#include <bits/stdc++.h>

using i64 = long long;
constexpr i64 mod = 998244353;
inline i64 qpow(i64 a, i64 b) {
    i64 v = 1;
    for (; b; b >>= 1, a = a * a % mod) {
        if (b & 1) v = v * a % mod;
    }
    return v;
}

constexpr int N = 2e6 + 10;
i64 fac[N + 1], ifac[N + 1];

inline i64 binom(int n, int m) {
    return fac[n] * ifac[n - m] % mod * ifac[m] % mod;
}
inline i64 f(int n, int m) {
    return (binom(n + m + 2, n + 1) - 1 + mod) % mod; 
}
inline i64 g(int n, int m) {
    return (f(n + 1, m + 1) - (n + 1) - (m + 1) - 1 - (i64)1 * (n + 1) * (m + 1) % mod + mod + mod) % mod;
}

int main() {
    fac[0] = 1;
    for (int i = 1; i <= N; i++) fac[i] = fac[i - 1] * i % mod;
    ifac[N] = qpow(fac[N], mod - 2);
    for (int i = N; i >= 1; i--) ifac[i - 1] = ifac[i] * i % mod;

    int W, H, L, R, D, U;
    scanf("%d%d%d%d%d%d", &W, &H, &L, &R, &D, &U);

    i64 ans = (g(W, H) - g(R - L, U - D) + mod) % mod;

    for (int x = L; x <= R; x++) {
        ans = (ans - f(W - x, H - D) * f(x, D - 1) % mod + mod) % mod;
    }
    for (int y = D; y <= U; y++) {
        ans = (ans - f(W - L, H - y) * f(L - 1, y) % mod + mod) % mod;
    }

    for (int x = L; x <= R; x++) {
        ans = (ans - f(W - x, H - (U + 1)) * f(x - L, U - D) % mod + mod) % mod;
    }
    for (int y = D; y <= U; y++) {
        ans = (ans - f(W - (R + 1), H - y) * f(R - L, y - D) % mod + mod) % mod;
    }

    printf("%lld\n", ans);
    return 0;
}