布隆过滤器
1 概述
了解缓存穿透的同学应该都或多或少的了解布隆过滤器吧。布隆过滤器是解决缓存穿透的一大利器。
2 缓存穿透及解决方案
缓存穿透:key对应的数据在数据源中并不存在,每次针对此key的请求从缓存获取不到,请求都会压到数据库,从而导致压垮数据库。
我们用到缓存的目的就是,减少数据库的压力,让能够从缓存中查询到的数据查询到之后就直接进行返回,查询不到在进行数据库的访问。但如果用一个不存在的用户id获取用户信息,不论缓存还是数据库都没有,若黑客利用此漏洞攻击可能压垮数据库。
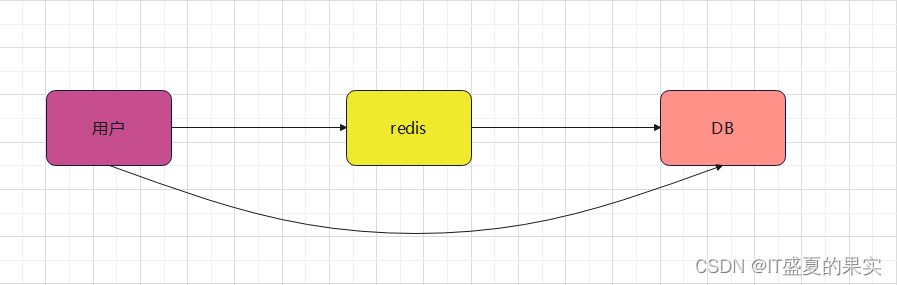
那么布隆过滤器是否能够解决缓存穿透问题呢?其实并不能够完全避免。因为只要用了redis,就不能避免缓存穿透。但是可以避免高频的缓存穿透。
举例:有人恶意攻击一个网站,拿一个不存在的id去访问,此时redis中肯定没有这条数据,就会去请数据库,而数据库中同样的也不可能有。假使他的访问频率比较高,那么就会对数据库造成很大的压力。
那么如何解决缓存穿透这个问题呢?第一种就是缓存空数据,第二种就是今天要说的布隆算法了。
2.1 缓存空数据
1)缓存空数据,当从redis中访问不到,再去数据库中也访问不到时,就在redis中存取一个null值,这样每回他再次访问的时候就直接将null返回了。
所以可以看出,当黑客通过一个固定的非法请求去攻击数据库,可以采用null值再次缓存的解决方案。
但是这样的攻击很容易被解决,也就可以看出来这个黑客的技术水平不是很高了。如果要是采用随机的请求方式去攻击的话,依然按照这种解决方案的话,就会在redis中存储了许多null值。占用内存空间不说,万一触发了redis的内存淘汰策略,就有可能清除掉redis中有价值的数据。
2.2 布隆过滤器
布隆过滤器:布隆过滤器是一种比较紧凑型的,比较巧妙的概率性数据结构,特点是高效的插入和查询,判断某样东西是否存在,他是用多个hash函数将一个数据映射到位图结构中,不仅可以提高查询效率,也可以节省大量的内存空间。
如果我们要映射一个值到布隆过滤器中,我们需要使用多个不同的哈希函数生成多个hash值、并对每个生成的hash值指向bit位置1,例如针对“Taobao”和3个不同的hash函数分别生成了3个hash值分别对应在位图下标第0,1,5的位置,用下图表示为:
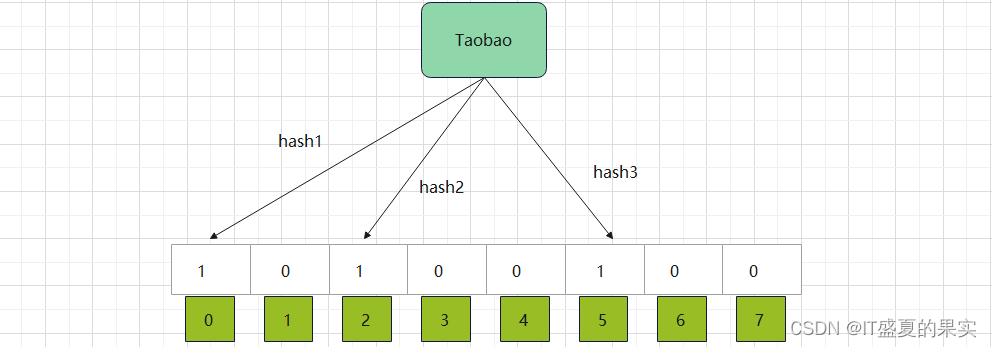
这只是存储了一个值,那么现在再存储一个值呢?比如再存储一个”Tianmao“值。”Tianmao“值也经过3个不同的hash函数生成了3个hash值对应在位图下标第1,2,6位置,用下图表示为:
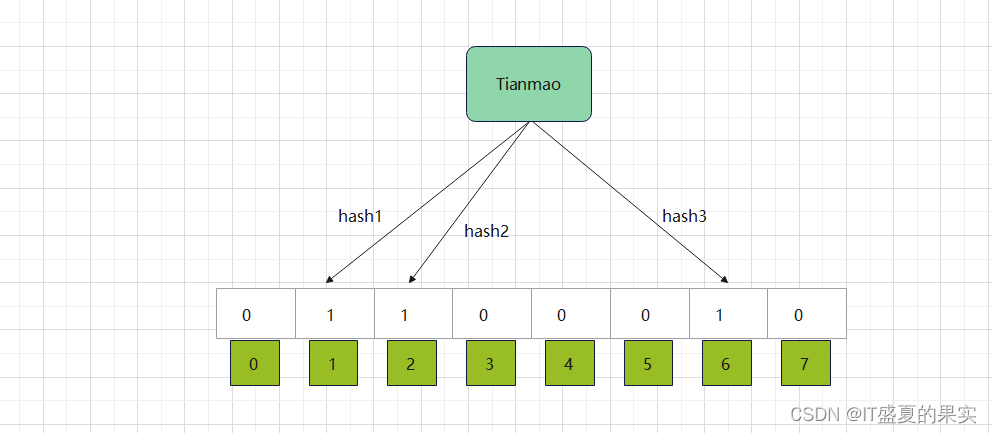
好,结合这两个值的存储,我们发现,第一个数值的hash位置在下标为2的地方与第二个数值的hash位置重合了。 以此来探讨下布隆过滤器的一些问题
问题一:当查找一个值的时候,返回的结果表明不存在,那么真的不存在吗?
答案:真的不存在。加入查询一个值“Hema”生成3个hash值所对应的下标为1,4,7。结果我们发现下标为4的这个bit位上值为0,说明没有任何一个值映射到这个bit位上。因此可以确定的说“Hema”不存在。
问题二:当查找一个值的时候,返回的结果表明存在,那么真的存在吗?
答案:不一定存在。因为hash碰撞的原因,hash值有可能重合。就拿上面两张图来说下标为2所对应的bit位上的值重合了。所以当你查询”Tianmao“的时候,发现3个bit位上的值都是1。有可能是其他的值填充的。所以当表名结果显示存在,不一定存在。
问题三:布隆过滤器支持删除吗?
传统的布隆过滤器并不支持删除操作。因为hash碰撞的原因,你想要删除的元素有可能存储着其他元素的信息。但是名为 Counting Bloom filter 的变种可以用来测试元素计数个数是否绝对小于某个阈值,它支持元素删除。
2.2.1 位图
在说布隆过滤器之前,不得不说一下位图这个数据结构。因为布隆过滤器就是通过位图+hash算法来实现的。
那么既然要说位图,肯定要直到它的作用以及它的实际应用。
假如现在有这样一个面试题:有10亿个无符号的整形数据,现在给定一个目标数字,判断这个数字是否在个10亿个数据中。
对于这样的问题,不同的同学给出了不同的解决方式,
解决方式一:说这么多的数据结构List,Map将数据全放进去,然后一个个的遍历,看它是否存在不就行了
解决方式二:还有的同学可能会说:将这些数字排序,然后进行二分查找
这样的解决方案可能会认为第二种解决方式比第一种的解决方式会高很多,不可否认的是的确是这样。但是大家都忽略了这样的一个问题,这么大量的数据,内存中放的下吗?
一个整形int就是4个字节,10亿个大概就需要4G的内存了,所以这种方式显然是行不通的!那就只能选择所占字符更小的了,char类型只占一个字节,但是这个治标不治本啊,依然是很大,于是我们引入了一种节省空间的数据结构,位图,他是一个有序的数组,只有两个值,0和1,0代表不存在,1代表存在。
bit 位 00000000
8bit = 1 byte (8位=1字节)
byte 1字节
shot 2字节
int 4字节
long 8字节
float 4字节
double 8字节
char java中2字节 (C语言中1字节)
boolean false/true(理论上1/8字节,实际上是占1字节)

2.2.2 位图+hash算法
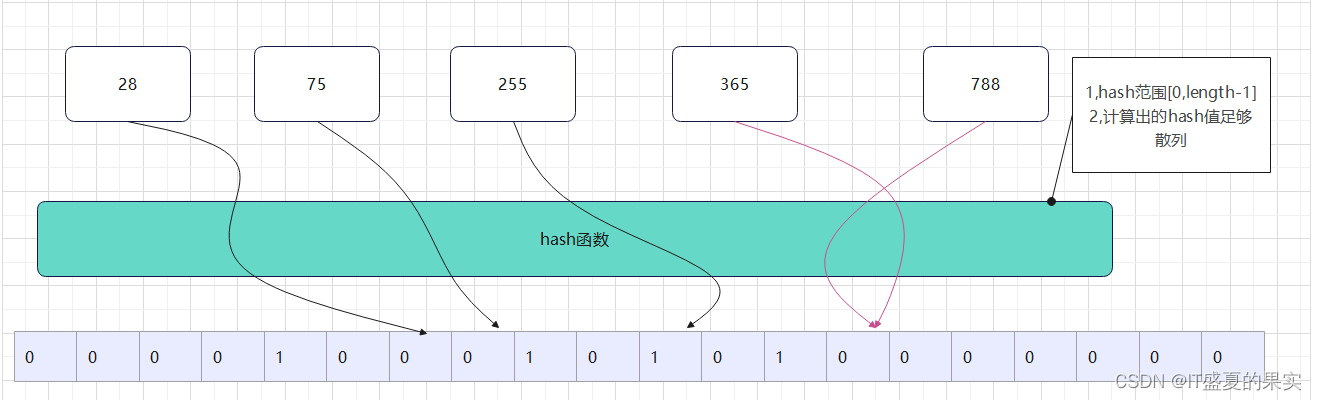
上图可以简要概括我们的布隆过滤器,数值经过hash函数计算出结果将数据映射到位图结构中。但是不同的数值计算有可能产生相同的hash值 (如图中红色的线表示),这种行为叫做hash冲突或者hash碰撞。
注意:hash函数自定义时需满足两个条件
1)hash值范围[0,length-1]
2)计算出的hash值足够散列
只有一个hash算法时: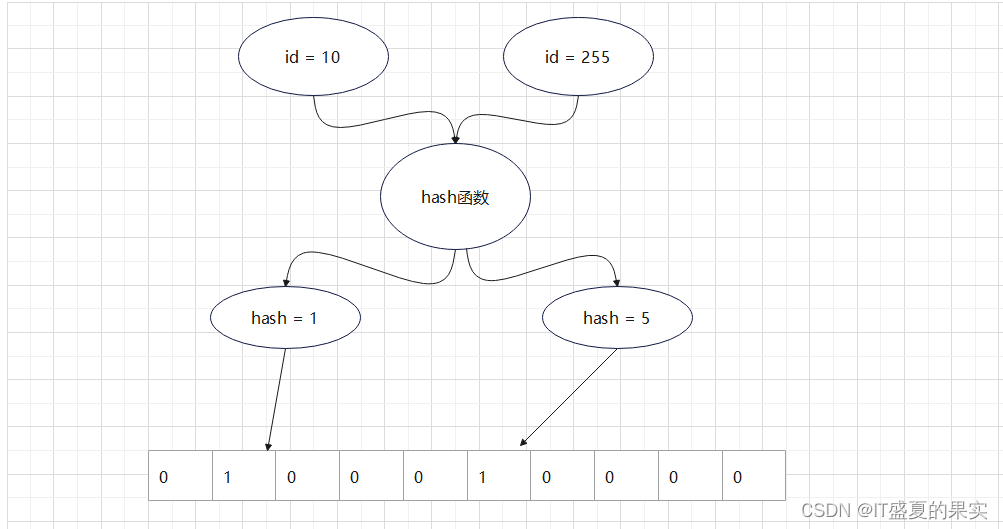
例如:当我们用id = 10时进行数据访问,此时经过hash算法算出hash值为1,就会在bit数组中下标为1的位置来标识数据 ,此时发现在下标为1的地方是有数据的,就将数据返回。(id = 255访问时也是如此)。但刚刚也讨论过,这个是有可能发生hash碰撞的。但是hash碰撞是不可避免的,只能减少hash碰撞的概率。减少hash碰撞的概率方式有两种一是加大数组的长度,二是增大hash函数的个数。假如id = 10这条数据经过3次hash计算,然后在位图上确定了3个位置。那么假如再来一个id = 166的数据,也计算它的3次hash值,然后在位图上确定了3个位置。那么它们通过第一次hash函数计算出来的结果可能相同,第二次通过hash函数计算出来的结果相同的概率就非常小了,第三次通过hash函数计算出来的结果要是还相同的话那概率真的是极低极低了。
有多个hash算法时:
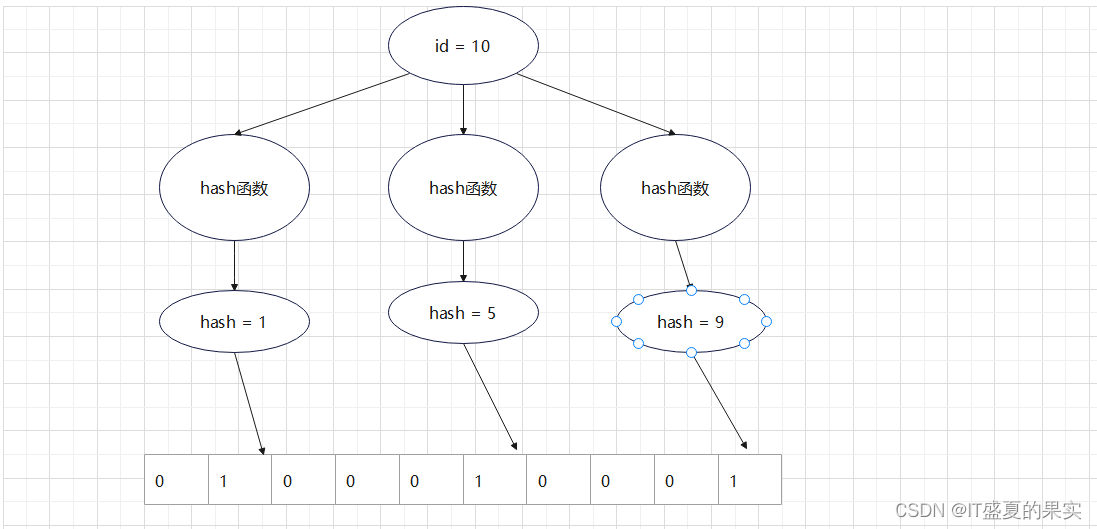
这个时候可能有人会问,一个数据的存储需要消耗3个位置,那么我们的bit数组岂不是会变的越来越长。内存也会随之而来越占越大。其实这是可以忽略的。因为bit数组本身占内存就是非常小的。
那么又有同学会问了,这样的话那我让他占的位数越多,那么发生hash碰撞的概率岂不是越小,那我让他占的位数多多益善不就行了 。其实这里要注意的是:hash函数的个数并不是越多越好,需要参考数组长度。
由上面的可知:我们利用布隆过滤器是存在一定的错误率的,因为hash碰撞的原因,它会有误判,即位图中不存在该数据,它也会误判成位图中存在该数据。但是布隆算法说不存在该数据,那么就一定不存在该数据。
2.3 代码演示
2.3.1 guava实现的布隆过滤器
用谷歌guava包中实现的布隆过滤器,这种方式的布隆过滤器是在本地内存中实现的。
引入相关依赖:
<dependency> <groupId>com.google.guava</groupId> <artifactId>guava</artifactId> <version>20.0</version> </dependency>
相关代码:
插入1千万条数据,误判率为0.01时:
package com.liubujun;
import com.google.common.hash.BloomFilter;
import com.google.common.hash.Funnels;
import java.text.NumberFormat;
/**
* @Author: liubujun
* @Date: 2022/3/8 15:57
*/
public class BloomFilterTest {
/** 预计插入的数据 */
private static Integer expectedInsertions = 10000000;
/** 误判率 */
private static Double fpp = 0.01;
/** 布隆过滤器 */
private static BloomFilter<Integer> bloomFilter = BloomFilter.create(Funnels.integerFunnel(), expectedInsertions, fpp);
public static void main(String[] args) {
long start = System.currentTimeMillis();
// 插入 1千万数据
for (int i = 0; i < expectedInsertions; i++) {
bloomFilter.put(i);
}
// 用1千万数据测试误判率
int count = 0;
for (int i = expectedInsertions; i < expectedInsertions * 2; i++) {
if (bloomFilter.mightContain(i)) {
count++;
}
}
// 创建一个数值格式化对象
NumberFormat numberFormat = NumberFormat.getInstance();
// 设置精确到小数点后2位
numberFormat.setMaximumFractionDigits(2);
String result = numberFormat.format((float) count / (float) expectedInsertions );
long end = System.currentTimeMillis();
long time = (end - start) ;
System.out.println("一共误判了:" + count);
System.out.println("误判率大概为:"+result);
System.out.println("耗时"+time+"毫秒");
}
}
测试结果:

bloomFilter断点结果:
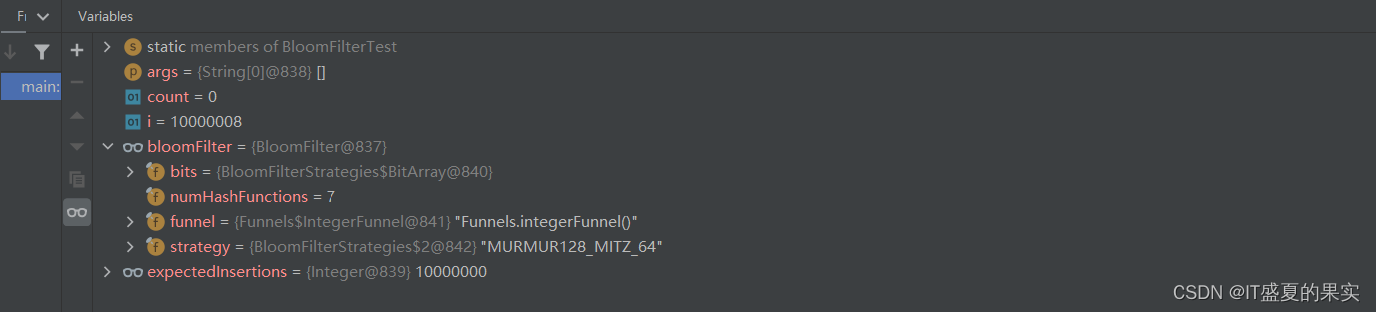
插入1千万条数据,误判率为0.03时:
测试代码:
/** 预计插入的数据 */
private static Integer expectedInsertions = 10000000;
/** 误判率 */
private static Double fpp = 0.03;
/** 布隆过滤器 */
private static BloomFilter<Integer> bloomFilter = BloomFilter.create(Funnels.integerFunnel(), expectedInsertions, fpp);
public static void main(String[] args) {
long start = System.currentTimeMillis();
// 插入 1千万数据
for (int i = 0; i < expectedInsertions; i++) {
bloomFilter.put(i);
}
// 用1千万数据测试误判率
int count = 0;
for (int i = expectedInsertions; i < expectedInsertions * 2; i++) {
if (bloomFilter.mightContain(i)) {
count++;
}
}
// 创建一个数值格式化对象
NumberFormat numberFormat = NumberFormat.getInstance();
// 设置精确到小数点后2位
numberFormat.setMaximumFractionDigits(2);
String result = numberFormat.format((float) count / (float) expectedInsertions );
long end = System.currentTimeMillis();
long time = (end - start) ;
System.out.println("一共误判了:" + count);
System.out.println("误判率大概为:"+result);
System.out.println("耗时"+time+"毫秒");
}测试结果:

bloomFilter断点结果: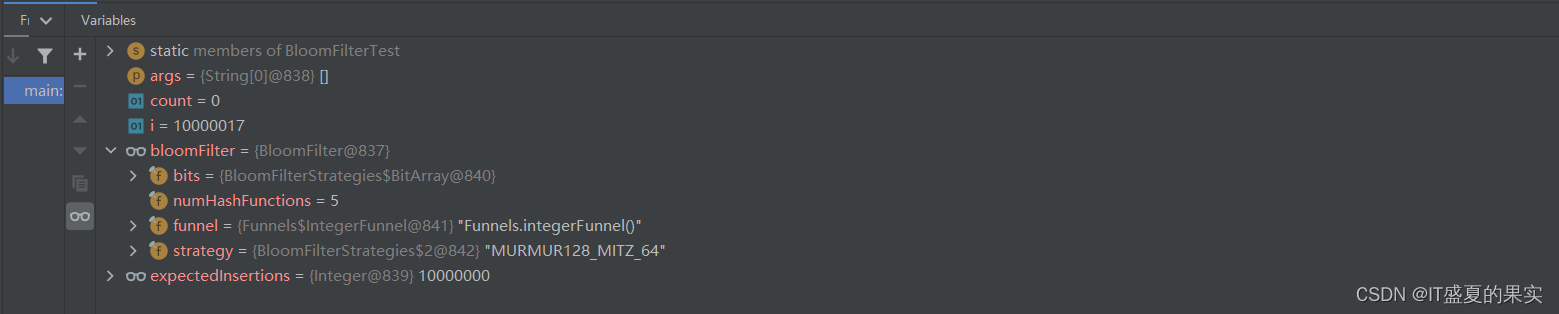
总结:当插入值的数量不变时,误差值越小,位组数越大,hash函数的个数越多,耗时越多。
注意:这个时候大家可能发现这个误差值是可以设置的,但是千万不能设成0,要根据实际情况,否则是非常耗时的。
2.3.2 redis实现的布隆过滤器
// Redis连接配置,无密码
Config config = new Config();
config.useSingleServer().setAddress("redis://124.221.89.80:6379");
// config.useSingleServer().setPassword("123456");
// 初始化布隆过滤器
RedissonClient client = Redisson.create(config);
RBloomFilter<Object> bloomFilter = client.getBloomFilter("user");
//初始化布隆过滤器:第一个参数:预计插入的数量,第二个参数,误判率
bloomFilter.tryInit(expectedInsertions, fpp);
//将号码10086插入到布隆过滤器中
bloomFilter.add("10086");
//判断下面号码是否在布隆过滤器中
System.out.println(bloomFilter.contains("123456"));//false
System.out.println(bloomFilter.contains("10086"));//true3 布隆过滤器的优缺点
布隆过滤器的优点:
1)增加和查询元素的时间复杂度为:O(K),(K为hash函数的个数,一般比较小),与数据量大小无关
2)hash函数硬件之间没有关系,方便硬件并行运算
3)布隆过滤器不需要存储元素本身,在某些对保密比较严格的场合有很大的优势
4)在能够承受一定误判的情况下,布隆过滤器比其他数据结构有很大的空间优势
5)数据量很大时,布隆过滤器可以表示全集,其他数据结构不能
6)使用同一组散列函数的布隆过滤器可以进行交,并,差运算
布隆过滤器缺点:
1)有误判率,即不能准确判断元素是否在集合中
2)不能获取元素本身
3)一般情况下,不能从布隆过滤器中删除元素
4)如果采用计数方式删除,可能会存在计数回绕问题



 浙公网安备 33010602011771号
浙公网安备 33010602011771号