[算法]KD树

KD树，你看着他好几个维度不明白，但实际上非常简单
\(K\)指维度 因此他可以在二维（多维）平面内进行搜索！！！

1.二维

1.1 建树

对于每一层，我们使用轮转法进行建树 什么意思呢？比如二维，如果\(x\)层为一维（横坐标），则\((x+1)\)层为二维（纵坐标）
确定好维数，接下来就是构建了。
此处用一张平面直角坐标系图来进行举例说明
已知二维平面点集\({(2,3),(5,4),(9,6),(4,7),(8,1),(7,2)}\)
首先进行排序，排完后如下：
\({(2,3),(4,7),(5,4),(7,2),(8,1),(9,6)}\)
将其作图，得：

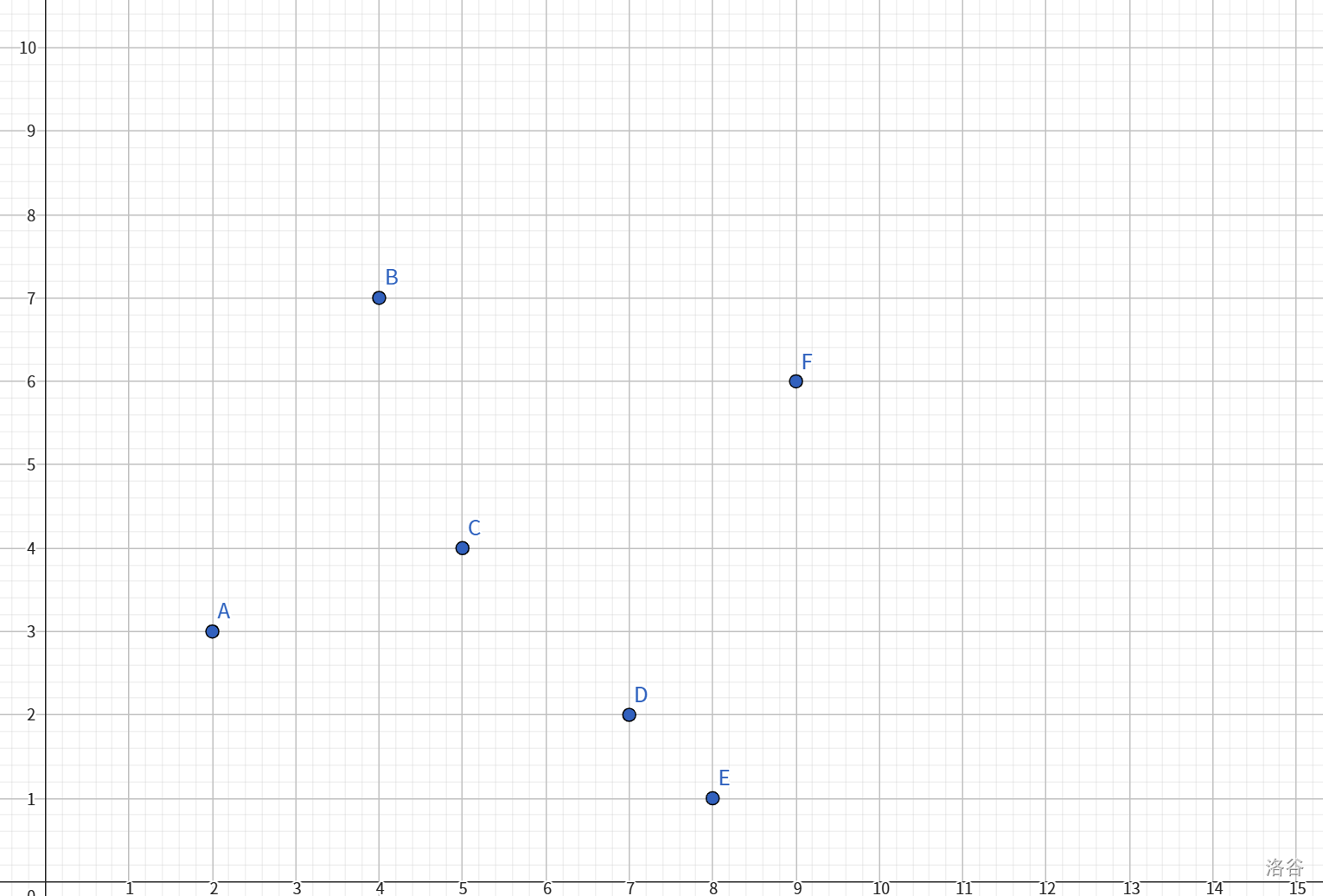
第一轮在\(x\)轴上进行划分（竖着切），找中点，得\((7,2)\)
则有图:

然后就有问题了
没法确定左右子树的根节点啊
于是递归
因为是第二轮，所以横着在\(y\)轴上划分
首先划分相对的左子树，找中点，得图：

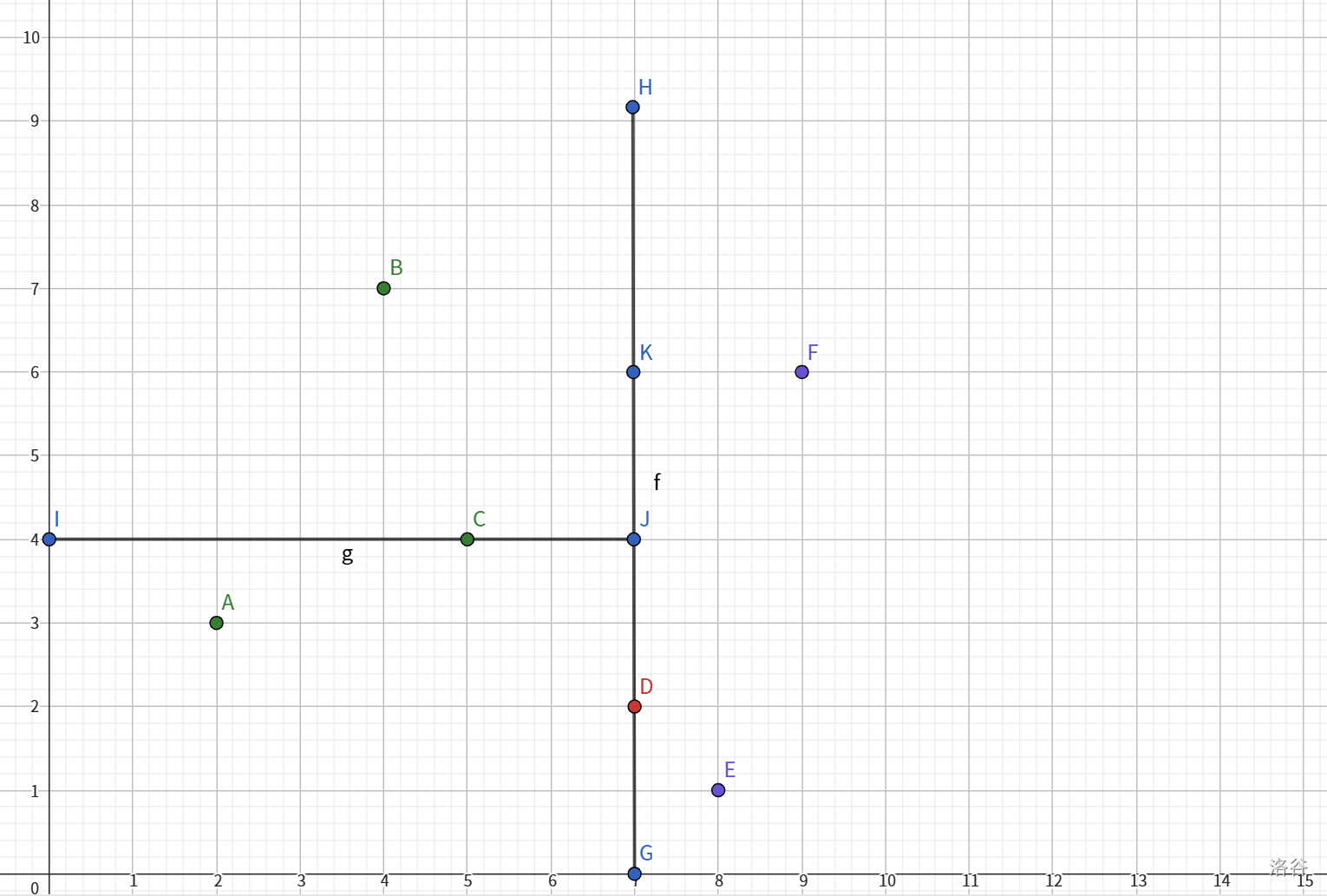
因此完整构建左子树
然后构建右子树（\(y\)轴）
两个点，我习惯性将在上的设为中点，则得图：

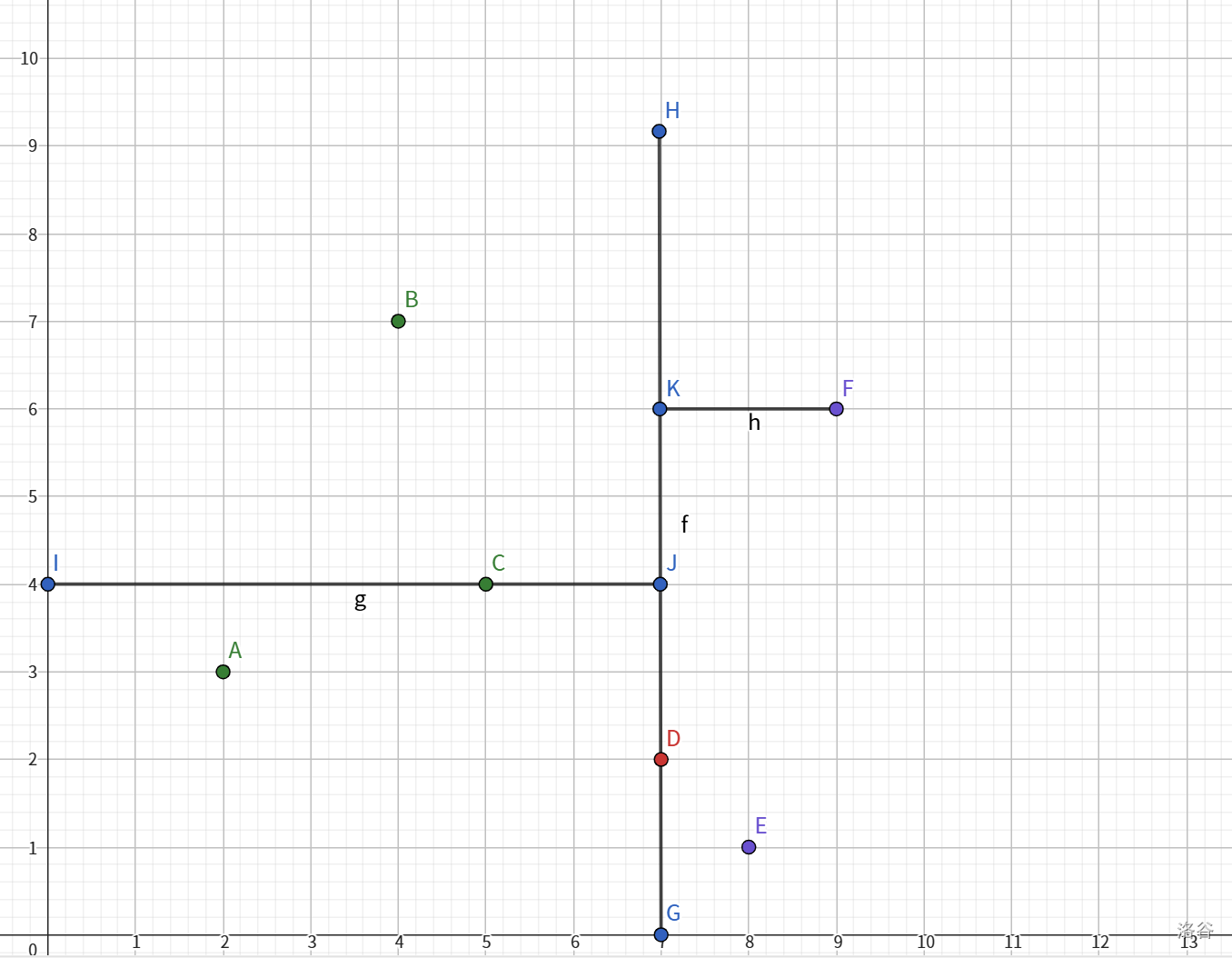
因此构建出树：

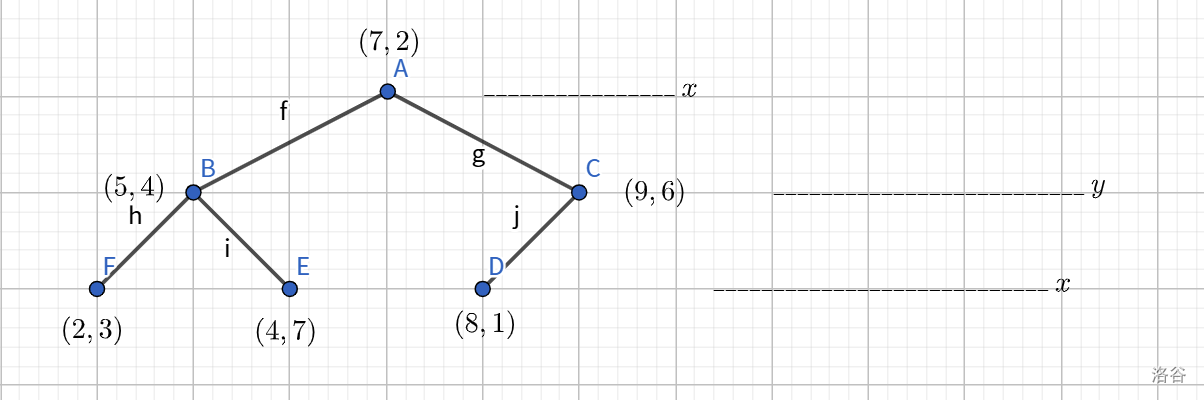
可以看到，每一次划分都用一条水平线或垂直线将平面分成相等的两部分（二分思想），得到的两个子空间单座左右节点，即二分过程

1.2 计算中位数

nth_element(ps+l,ps+mid,ps+r)解决的问题不必多讲 但是不会排序数组！！！

1.3 代码

struct kdTree {
    point p;          // 直接存储对象
    kdTree ls, rs;    // 对象实例
};

/kdtree-build
void build(int l, int r, int rt = 1, int dep = 0)
{
    if (l > r)
        return;
    son[rt] = r - l;                    // 当前节点子树元素数量
    son[rt * 2] = son[rt * 2 + 1] = -1; // 初始化子节点为无效值
    idx = dep % k;                      // 根据深度决定当前分割维度
    int mid = (l + r) / 2;              // 计算当前区间中点

    // 快速选择算法，将中位数元素放到mid位置
    nth_element(po + l, po + mid, po + r + 1);
    pt[rt] = po[mid]; // 当前节点存储中位数点

    // 递归构建左右子树
    build(l, mid - 1, rt * 2, dep + 1);     // 左子树区间[l,mid-1]
    build(mid + 1, r, rt * 2 + 1, dep + 1); // 右子树区间[mid+1,r]
}

2.插入

2.1 思路

与二叉查找树类似，假设现在要将新增点插入到节点\(x\)的子树中，那么通过比较新增点的大小，来确定是左/右子树
（小左大右）

2.2 代码

void insert(kdTree* &o,const point &p)
{
    if(o==nullptr)  // 当前节点为空时创建新节点
    {
        o=new kdTree(p); // 初始化新节点存储目标点
        return;
    }
    int d=cmp(p,o->p)^1; // 比较当前维度坐标（异或1实现维度交替）
    dimension ^=1;        // 切换分割维度
    insert(o->ch[d],p);   // 递归插入对应子树
    o->maintain();        // 更新节点统计信息（如子树大小等）
}

3.查询

3.1 思路

对于每个节点，判断其对应的k维超矩形是否与查询超矩形有交集。
1.如果当前超矩形与查询超矩形不相交，则跳过该节点。
2.如果当前超矩形完全包含在查询超矩形内，则将该节点及其子树中的所有点添加到结果集。
3.如果当前超矩形与查询超矩形部分相交，则递归查询左右子树。


ps.超矩形你可以理解为一大块空间，放到二维上比

3.2 代码

可惜啦 这里没有代码
这就是\(manacher\)的思路，回去好好想想，看看自己是否学会！

4.查找最近/远点

4.1 思路

这里以查找远点为例，就是由远及近的一个思想，看着代码理解

4.2代码

void query(kdTree* o,const point &p)
{
    if(o==nullptr) return;
    ans=min(ans,dis(o.p,p));       // 更新最近距离
    int d=o.ls.dis(p)>o.rs.dis(p); // 比较左右子树到目标点的距离，选择更远的分支
    query(o.ch[d],p);              // 优先搜索更远的分支（剪枝优化）
    if(o.ch[d^1].dis(p)<ans)       // 检查另一分支是否可能有更近点
        query(o.ch[d^1],p);        // 递归搜索另一分支
}

5.例题

1.摆棋子
2.查找k远点
都是模板题，只不过一个是远，一个是近，这里就不解析了（反正也是模板题

完结撒花！！！