DFS

200. 岛屿数量

 

给定一个由 '1'（陆地）和 '0'（水）组成的的二维网格，计算岛屿的数量。一个岛被水包围，并且它是通过水平方向或垂直方向上相邻的陆地连接而成的。你可以假设网格的四个边均被水包围。

示例 1:

输入:
11110
11010
11000
00000

输出: 1
示例 2:

输入:
11000
11000
00100
00011

输出: 3

 

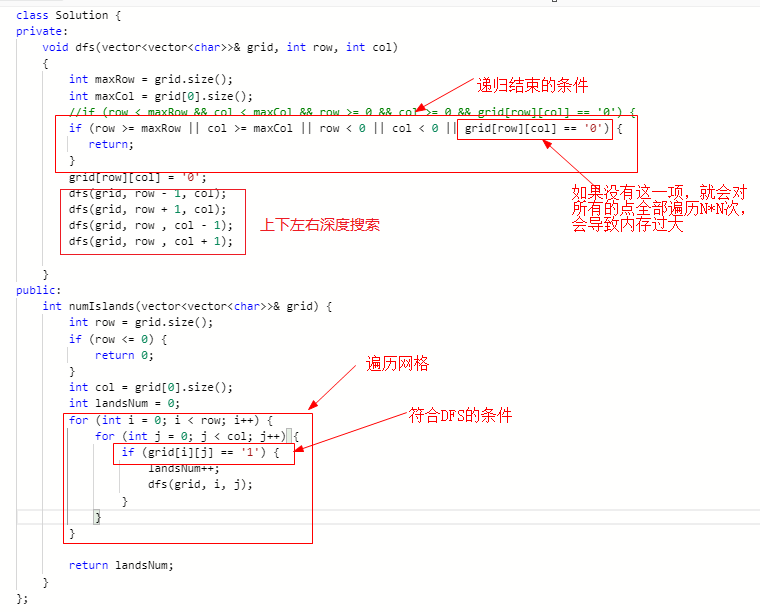
 官方题解：

DFS

方法一：深度优先搜索 【通过】

将二维网格看成一个无向图，竖直或水平相邻的 1 之间有边。

线性扫描整个二维网格，如果一个结点包含 1，则以其为根结点启动深度优先搜索。在深度优先搜索过程中，每个访问过的结点被标记为 0。计数启动深度优先搜索的根结点的数量，即为岛屿的数量。

class Solution {
private:
  void dfs(vector<vector<char>>& grid, int r, int c) {
    int nr = grid.size();
    int nc = grid[0].size();

    grid[r][c] = '0';
    if (r - 1 >= 0 && grid[r-1][c] == '1') dfs(grid, r - 1, c);
    if (r + 1 < nr && grid[r+1][c] == '1') dfs(grid, r + 1, c);
    if (c - 1 >= 0 && grid[r][c-1] == '1') dfs(grid, r, c - 1);
    if (c + 1 < nc && grid[r][c+1] == '1') dfs(grid, r, c + 1);
  }

public:
  int numIslands(vector<vector<char>>& grid) {
    int nr = grid.size();
    if (!nr) return 0;
    int nc = grid[0].size();

    int num_islands = 0;
    for (int r = 0; r < nr; ++r) {
      for (int c = 0; c < nc; ++c) {
        if (grid[r][c] == '1') {
          ++num_islands;
          dfs(grid, r, c);
        }
      }
    }

    return num_islands;
  }
};

　　

复杂度分析

时间复杂度 : O(M\times N)O(M×N)，其中 MM 和 NN 分别为行数和列数。

空间复杂度 : 最坏情况下为 O(M \times N)O(M×N)，此时整个网格均为陆地，深度优先搜索的深度达到 M \times NM×N。

方法二: 广度优先搜索 【通过】
算法

线性扫描整个二维网格，如果一个结点包含 1，则以其为根结点启动广度优先搜索。将其放入队列中，并将值设为 0 以标记访问过该结点。迭代地搜索队列中的每个结点，直到队列为空。

class Solution {
public:
  int numIslands(vector<vector<char>>& grid) {
    int nr = grid.size();
    if (!nr) return 0;
    int nc = grid[0].size();

    int num_islands = 0;
    for (int r = 0; r < nr; ++r) {
      for (int c = 0; c < nc; ++c) {
        if (grid[r][c] == '1') {
          ++num_islands;
          grid[r][c] = '0'; // mark as visited
          queue<pair<int, int>> nei***ors;
          nei***ors.push({r, c});
          while (!nei***ors.empty()) {
            auto rc = nei***ors.front();
            nei***ors.pop();
            int row = rc.first, col = rc.second;
            if (row - 1 >= 0 && grid[row-1][col] == '1') {
              nei***ors.push({row-1, col}); grid[row-1][col] = '0';
            }
            if (row + 1 < nr && grid[row+1][col] == '1') {
              nei***ors.push({row+1, col}); grid[row+1][col] = '0';
            }
            if (col - 1 >= 0 && grid[row][col-1] == '1') {
              nei***ors.push({row, col-1}); grid[row][col-1] = '0';
            }
            if (col + 1 < nc && grid[row][col+1] == '1') {
              nei***ors.push({row, col+1}); grid[row][col+1] = '0';
            }
          }
        }
      }
    }

    return num_islands;
  }
};

　　

复杂度分析

时间复杂度 : O(M \times N)O(M×N)，其中 MM 和 NN 分别为行数和列数。

空间复杂度 : O(min(M, N))O(min(M,N))，在最坏的情况下（全部为陆地），队列的大小可以达到 min(M，NM，N)。

作者：LeetCode
链接：https://leetcode-cn.com/problems/number-of-islands/solution/dao-yu-shu-liang-by-leetcode/
来源：力扣（LeetCode）