容斥原理学习笔记
数数菜鸡在线丢人。
由于一道计数题都不会做,做别的题又时不时碰到容斥,我决定深入学一学这个东西。
这个博主的数数能力比较拉垮,要是写的那里比较 naive 了还请喷的轻一点。
从小学数学开始
我们小学数学讲过这样的东西,
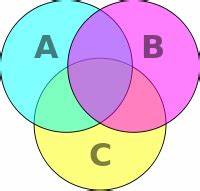
我们只要拥有 A 属性的物品数量、拥有 B 属性的物品数量、拥有 C 属性的物品数量、同时拥有某两个属性的物品数量、同时拥有三个属性的物品数量,让我们求总物品数量。
小学数学老师会告诉你,先把拥有一个属性的物品数量全加起来,再用拥有某两个属性的物品数量减去多算进去的,再用拥有三个属性的物品数量补偿多减去的。
那么我们扩展到 \(k\) 个属性呢?我们形式化的描述一下题意:设 \(k\) 个属性的集合为 \(U\),我们已知 \(F(S)\) 表示至少拥有属性集合 \(S\) 的物品数量(假设每个物品都有属性),求拥有至少一个属性的物品数量。
我们依照小学数学的思路,答案就是
很神奇哦,这时候是不是应该去深究一下这个 \((-1)^{|S|+1}\) 是怎么来的。从本质上理解的话,那么我们给属性集合 \(S\) 一个容斥系数 \(f(|S|)\),我们要让某一个拥有 \(n\) 个属性的物品只被算 \(1\) 次,然后考虑这个物品被那些属性集合枚举到,可以得到
一个合理的构造就是 \(f(i)=(-1)^{i+1}\)。反向推回去可以证明是对的。
一般化的容斥
通过容斥可以数很多东西,我们下文以“物品”为数数对象,当然可以以是方案、路径、数字等等;同样的,“条件”也不过是属性、限制一类词的统称,毕竟本质上是一样的。
假设我们有 \(n\) 个条件 \(A_1\dots A_n\),和物品集合 \(S\)。泛泛的讲,我们应该考虑每一个物品应该的贡献,计数答案的形式往往是
其中 \(c(x,A_i)\) 表示物品 \(x\) 在 \(A_i\) 条件下的贡献,\(f(A_i)\) 则表示 \(A_i\) 条件的容斥系数。当然你也可以当废话看。
一般情况下每个物品在某个条件下的贡献是 \(0/1\)。
因为题目中往往让我们计算 \(S\) 中满足条件 \(A_0\) 的物品数,而我们只能够求得一些限制较为宽裕的条件 \(A_1\dots A_n\) 的物品数,我们设为 \(s(A_i)\),所以我们要通过容斥系数,让每个物品贡献到应该贡献的地方,即
这个容斥系数怎么求,也就是计数问题的重点。不同的问题有不同的解法,不过还是有迹可循的。
刚开始的时候会有些晕,晕的时候一定要抓住计数对象是谁、条件是谁,搞清楚每一步已知什么、在求什么。
例子 1
求有多少个长为 \(n\) 的排列 \(a_1\dots a_n\) 满足 \(a_i\neq i\)。
也就是求恰好 \(0\) 个位置满足 \(a_i=i\) 的排列数。“恰好”的条件不好求,但是“至少”是好求的,至少 \(i\) 个位置满足 \(a_i=i\) 的排列数显然是 \(\displaystyle {n\choose i}(n-i)!\)。
然后要计算容斥系数,考虑一个有 \(m\) 个位置满足 \(a_i=i\) 的排列的贡献:在“恰好 \(m\) 个位置满足 \(a_i=i\)”条件中贡献为 \([m=0]\),在 \(\forall i\le m\) 的“至少 \(i\) 个位置满足 \(a_i=i\)”条件中贡献为 \({m\choose i}\)。
设 \(f_i\) 表示至少 \(i\) 个位置满足 \(a_i=i\) 条件的容斥系数,\(g_i\) 表示恰好 \(i\) 个位置满足 \(a_i=i\) 条件的答案贡献,可以得到
在这里 \(g_m=[m=0]\),然后可以通过 \(\mathcal O(n^2)\) 递推、打表找规律,或者大力二项式反演求得 \(f_i\),
最后答案就是 \(\sum_{i=0}^n{n\choose i}(n-i)!(-1)^i\)。
例子 2
求 \([1,n]\) 中能被 \(a_1\dots a_m\) 中的奇数个数整除的数个数。
\(1\le n\le 10^9\),\(1\le m\le 15\)。
首先枚举 \(\{a_i\}\) 的子集 \(S\),就容易得到至少被 \(|S|\) 个数整除的数的个数为 \(\lfloor\frac{n}{\operatorname{lcm}S}\rfloor\)。
类似的思路,若有一个恰好能被 \(k\) 个 \(a_i\) 整除的数,它的贡献应该是 \(k\bmod 2\),所以得到容斥系数的计算式为
考虑到 \(m\) 很小,所以直接 \(\mathcal O(m^2)\) 递推。递推式很好得到,首先 \(f_0=0\),然后把 \(f_k\) 项拆出来,
例子 3
在找了在找了……
一点总结
可以发现,我们先转化题目条件,求出若干较为好满足的条件的答案,条件之间的转化常见的有:
- \(=\) 和 \(\neq\)(\(\ge\)、\(\le\))
- \(\min\) 和 \(\max\)
- “恰好” 和 “至少”
然后往往是从一个物品应该的贡献出发,得到容斥系数的计算式,然后通过递推,或是递推打表后找规律,或是直接反演得到容斥系数。
对于很多数据范围很大的题目,容斥系数的计算式有一些很常见的形式,对应着一些基本的反演类型:
-
组合数形式(二项式反演)
\[\sum_{i=0}^m{m\choose i}f_i=g_m \] -
倍数形式(莫比乌斯反演)
\[\sum_{d|m}f_d=g_m \] -
斯特林数形式(斯特林反演)
\[\sum_{i=1}^m{m\brace i}f_i=g_m \] -
集合形式(子集反演)
\[\sum_{T\subseteq S}f_T=g_S \]
例题
BZOJ#4671 异或图
给出 \(s\) 个图,求有多少个图的集合满足异或和是一张连通图。
这里图的异或相当于边集的异或,若 \(G_1\operatorname{xor} G_2=G_3\),一条边存在于 \(G_3\) 当且仅当在 \(G_1,G_2\) 的出现次数和为 \(1\)。
\(1\le n\le 10\),\(1\le s\le 60\)。
“一张连通图”翻译为“连通块个数恰好为 \(1\)”。
我们还是先满足“至少”的条件:枚举点集的划分,假设划分为 \(k\) 个集合,那么就是要求不同集合之间的点不能连边,集合之内随意。设这样一条不允许连的边在这 \(s\) 个图的取值分别为 \(a_i\),我们可以得到一个异或方程 \(a_1x_1\operatorname{xor} a_2x_2\operatorname{xor}\dots a_sx_s=0\)。最后形成一个异或方程组,方案数就是 \(2^{\text{自由元个数}}\)。可以通过高斯消元或者线性基求。
接下来考虑一张拥有 \(m\) 个连通块的图的贡献,得到容斥系数的计算式
这里 \(g_m=[m=1]\)。识别为斯特林数形式,斯特林反演得到
这道题就可以 \(\mathcal O(B_nn^2)\) 做了,\(B_n\) 为贝尔数,即划分的方案数。
P3349 [ZJOI2016]小星星
给出一张图 \(G\) 和一棵树 \(T\),点数都为 \(n\),求有多少个长为 \(n\) 的排列 \(\{a_i\}\),满足若存在 \(\langle u,v\rangle \in T\) 则一定有 \(\langle a_u,a_v\rangle \in G\)。
\(n\le 17\)。
题意转化一下,就是给树上每一个点分配一个编号,并且相邻的点有编号的限制,要求最后编号无重复。
一开始不太容易想到要容斥,不妨先考虑暴力状压 DP。设 \(f(u,i,S)\) 表示 \(u\) 点编号为 \(i\),且以 \(u\) 为根的子树的编号集合为 \(S\),的方案数。转移就是对几个不相交的集合的合并。显然这样复杂度是爆炸的,但是已经没有优化的余地了。
这时候容斥的作用就显现了,我们可以先放宽限制来降低复杂度,然后容斥来得到最终答案。我们可以瞅准转移时“集合不相交”的限制,但是去掉了这个限制的话,编号会重复,编号集合的大小小于 \(n\)。
这时候有容斥的味道了。我们发现要求的是编号集合大小等于 \(n\),而现在只能得到编号集合大小小于等于 \(n\) 的方案数。于是构造若干个限制:枚举编号集合 \(S\),钦定整棵树的编号集合为 \(S\) 的子集。\(\mathcal O(n^3)\) DP 一下可以得到 \(s(S)\) 表示整棵树编号集合为 \(S\) 的子集的方案数。
上套路,设大小为 \(n\) 的编号集合为 \(U\),对于一个编号集合恰好为 \(S\) 的方案,正确的贡献应该为 \([S=U]\),得到容斥系数计算式
识别为集合形式,子集反演可以得到容斥系数
最后答案就是 \(\sum_{S\subseteq U}s(S)f(T)\)。
于是我们得到了 \(\mathcal O(n^32^n)\) 的做法,实际上跑的飞快。
在咕了在咕了……


 浙公网安备 33010602011771号
浙公网安备 33010602011771号