fhq-Treap学习笔记

前言

FHQ-Treap不是区，它是基于笛卡尔树利用分裂和合并来实现平衡的平衡树

我写这篇随笔是因为我在上whk期间手推出了我之前一辈子也不会的fhq-treap，~~由于太兴奋被老师逮着了~~，遂写此文

啥是 fhq-treap

网络上关于treap和fhq-treap的教程已经够多了。这里就只讲一下最基本的 \(fhq-Treap\) 的板子及其原理

首先 \(fhq-Treap\) 肯定是基于 \(Treap\) 的一个改进版本，而 \(fhq\) ，范浩强就是这个数据结构的发明人。

啥是 Treap

Treap由两个名词合并而来 \(tree\) 树， \(heap\) 堆 , 那么顾名思义，这玩意就是同时满足二叉搜索树和堆的性质的一棵树。

先讲讲万恶之源二叉搜索树，这个东西很简单左子树永远小于父亲，右子树永远大于父亲(具体视情况而定)

ok，现在又得到一个问题了，为什么要结合二者呢。因为对于二叉搜索树来讲，对于一个序列，插入节点的顺序不同会导致树的形态的不同，因此可能会退化成为一条链。
所以 \(Treap\) 的使命就是优化插入，使其尽可能能卡满整个二叉树使得树高来到 \(log_2 n\)

原理

对于那么多的概念其实没有必要理解那么透彻。因为学完之后再来看上面的部分应该更好理解一点。在 \(treap\) 中有两个关键值 \((val,rnk)\) , 这里有的教程会和这里不同。

在 \(treap\) 中, 节点中的 \(val\) 满足二叉搜索树的性质，而 \(rnk\) 满足二叉堆的性质。

啥意思呢，且看下面的一张图

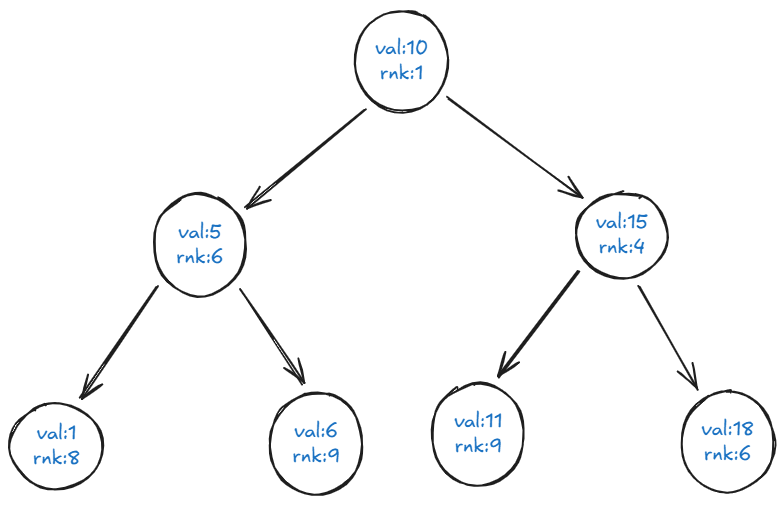
其中对于任意节点的左字数里的任意节点的 \(val\) 都比当前节点的 \(val\) 的大。
而对于任意节点的子节点的 \(rnk\) 都比自身的 \(rnk\) 要大。（即一个小根堆，具体实现随便大根堆还是小根堆都行）。

那要如何维护这一颗树呢？

首先对于每一个节点，他的 \(val\) , 一般是会给定的 , 那么 \(rnk\) 只要随机生成一个数就行了。

重头戏来了，如何做到插入节点并保持这棵树的性质呢？
对于 \(Treap\) 来讲，它是靠左旋与右旋来保证的。这一部分比较抽象（~~可能是我太蒻了~~），而 \(fhq-Treap\) 就解决了这一个问题。它的码量不仅小，而且通俗易懂，并且能完成 \(Treap\) 能完成的工作，只不过常数可能大一点。

\(fhq-Treap\)

接下来就细说 \(fhq-Treap\) 的基本逻辑,首先是它的基本操作 \(split\) 和 \(merge\) , 分裂与合并

基本结构

基本的 \(fhq-Treap\) 代码的结构如下， \(cnt\) 表示总共生成的节点总数（没有进行内存优化），\(root\) 表示树的根。

struct node{
	ll val , rnk , ls , rs , siz;
};

struct fhq{
    node tree[kMaxN];
    ll cnt , root;
    ...
}

\(addnode\) 操作

这个操作是 \(fhq-treap\) 的基石，含义顾名思义

代码

	ll addnode(ll val){
		tree[++cnt] = {val , rand() , 0 , 0 , 1};
		return cnt;
	}

\(pushup\) 操作

如果说 \(split\) 和 \(merge\) 操作给予了 \(fhq-Treap\) 行动的肌肉，那么 \(pushup\) 就是 \(Treap\) 的骨架。

对于很多平衡树类的题目常常要维护节点上除了 \(val\) 的其他信息，这一些信息会被增加节点与删除节点所改变，那么就需要 \(pushup\) 来更新这些信息。
比如在普通平衡树模版题里，要额外维护的信息就是 \(siz\) , 树的大小，那么此时就需要 \(pushup\) 来维护。

显然，如果当前节点 \(p\) , 的左右儿子的 \(siz\) 信息是最新的，那么只需要 \(p.siz \leftarrow p.l.siz + p.r.siz + 1\) 即可

代码如下

  void pushup(ll p){
	tree[p].siz = tree[tree[p].ls].siz + tree[tree[p].rs].siz + 1;
  }

\(split\) 操作

给定一颗值域在 \([1,n]\) 的\(Treap\)，进行一次 \(split\) 操作，参数为 \(val\) , 就能得到值域在 \([1,val]\) 与 \((val,n]\) （在整数范围内等价于 \([val + 1,n]\)）的两颗\(Treap\)

令 \(x\) 表示值域在 \([1,val]\) 的 \(Treap\) 的根, \(y\) 表示值域在 \((val , n]\) 的 \(Treap\) 的根。即 \(x\) 内的所有节点都比 \(y\) 内的所有节点要小
现在考虑实现(split的参数val用v表示)：

对于 \(val \leq v\) 的话，那么它就包括它的左子树就划分到 \(X\) 中去，接着向右边递归
对于 \(val > v\) 的话，那么包括它和他的右子树就要划分到 \(Y\) 中去，然后向左边递归

难道真的只有这么简单吗，答案是否定的，对于 \(val \le v\) 时，可能它的右子树中的一个节点满足 \(\leq v\) , 像下面的动图那样。

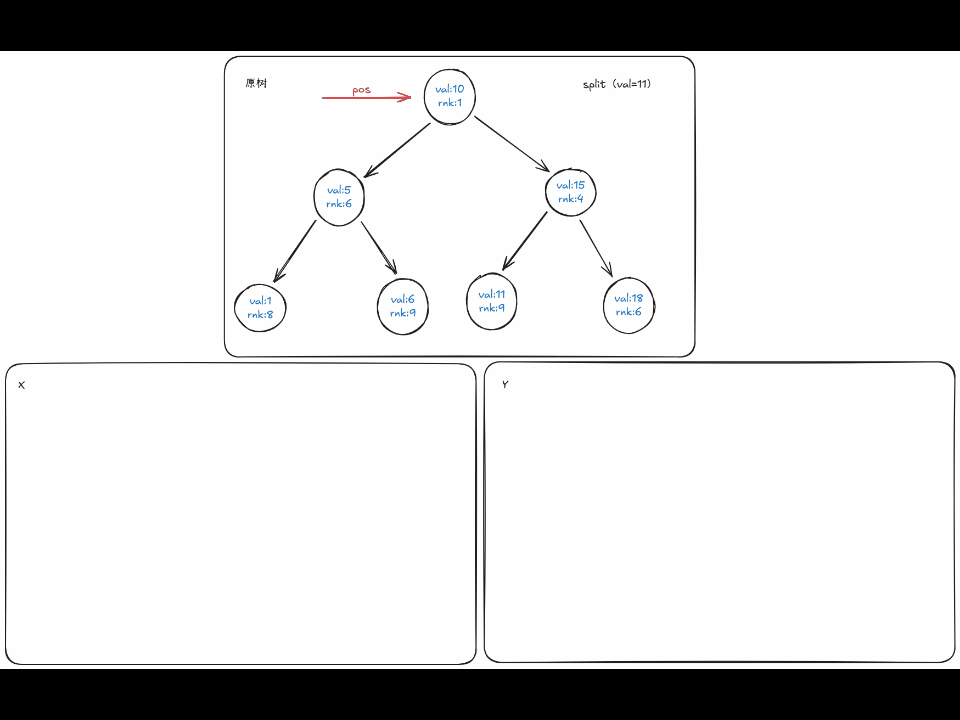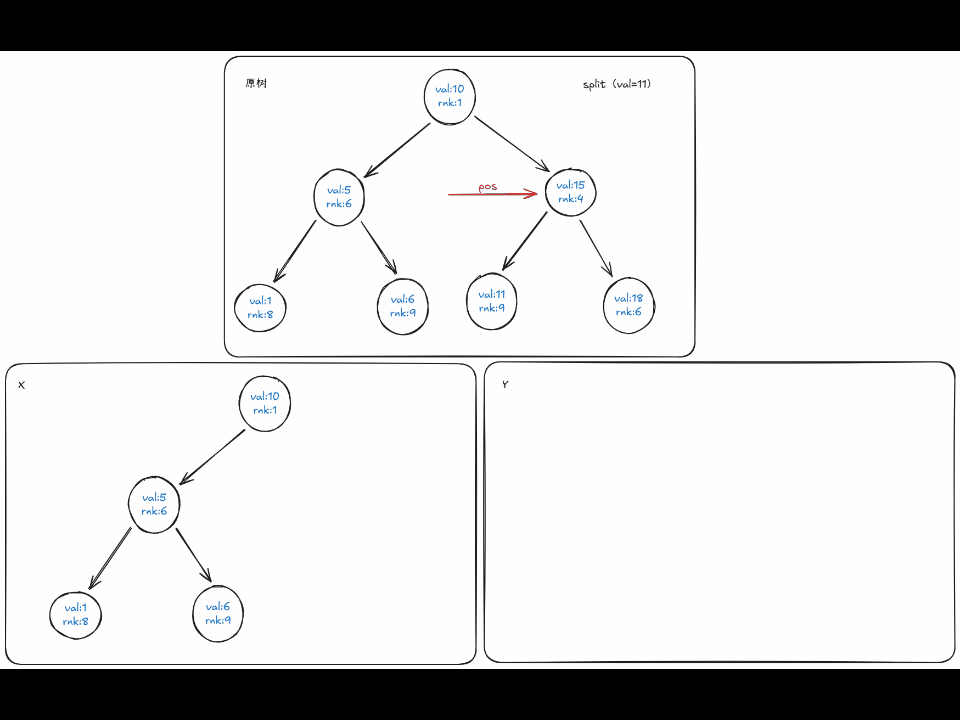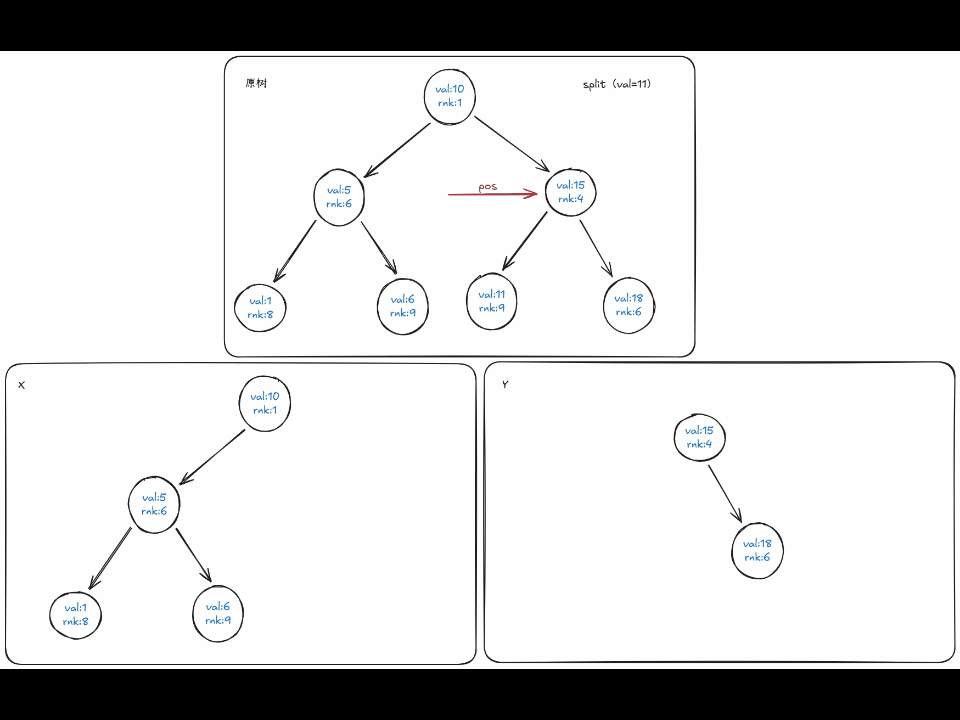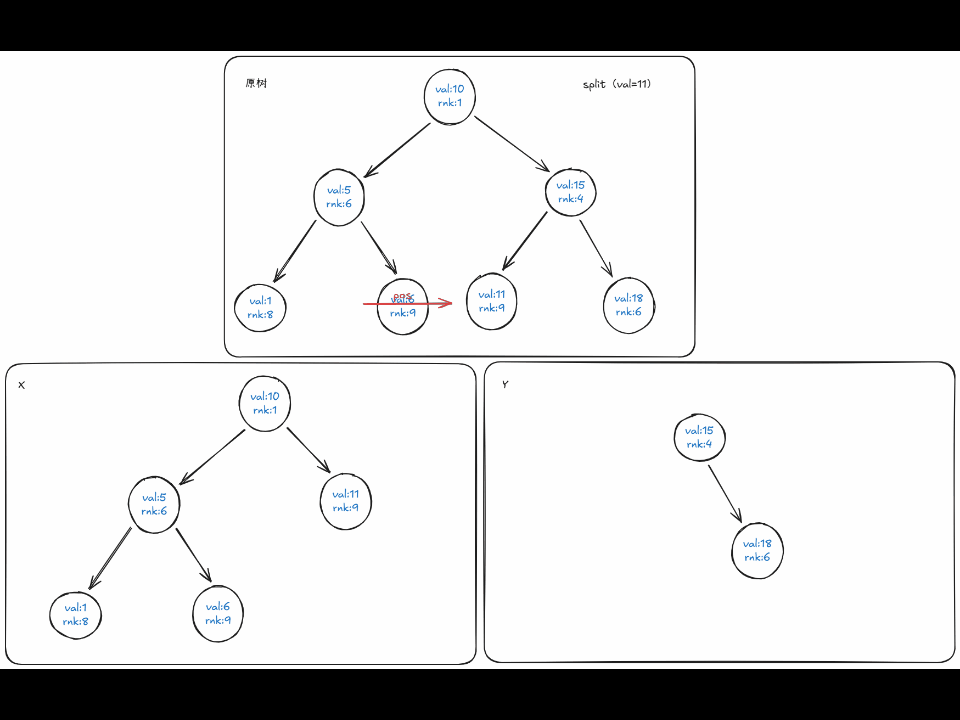
合并结果_1

定义 \(split(pos,val)\) 表示在递归到 \(pos\) 时，按 \(val\) 分割，返回的 \(x,y\) , 由于函数的返回值有两个，因此一般在实现里通过传引用的方式来实现
一般写成这样 ll split(ll now , ll&x , ll&y , ll val)

因此我们需要在递归时将 \(x , y\) 作为参数进行传入，具体的：

当 \(now.val \leq val\) 时，右子树没有被划分，\(x \leftarrow now\) , 然后因为是在 \([1,val]\) 之内，所以递归执行 split(now.r , now.r , y , val)
当 \(now.val > val\) 时，左子树没有被划分，\(y \leftarrow now\) , 然后因为是在 \((val,n]\) 之内，所以递归执行 split(now.l , x , now.l , val)

虽然上面看上去很绕但是看一遍代码思路就明了了

	void split(ll now , ll &x , ll &y , ll val){
		if(!now) { // 节点没了，肯定就不会执行下去了
			x = y = 0;
			return;
		}
		if(tree[now].val <= val){
			x = now;
			split(tree[now].rs , tree[now].rs , y , val);
		}else{
			y = now;
			split(tree[now].ls , x , tree[now].ls , val);
		}
		pushup(now);
	}

\(merge\) 操作

~~天下大势，分久必合，合久必分~~

有了分裂，那么就一定有合并~~不然我写fhq-treap干嘛~~

定义函数 \(merge(u,v)\) , 表示将以 \(u\) 为根的树与以 \(v\) 为根，并且保证 \(u\) 内的所有节点小于 \(v\) 内的所有节点，返回值是合并后的根，通常写成 ll merge(ll u , ll v)
合并是按照堆的规则进行合并的，然而 \(rnk\) 最后为什么堆不重要（即大根堆小根堆随意）,因为 \(rnk\) 的是随机值，因此 \(Treap\) 的平衡性是靠平衡保证的。

大体思路是这样的：

若满足 \(u\) 做根节点，则 \(u.r \leftarrow merge(u.r,v)\)
若满足 \(v\) 做根节点，则 \(v.l \leftarrow merge(u,v.l)\)

我一般是作为小根堆来维护了，因此满足 \(u\) 做根节点的条件是 \(u.rnk < v.rnk\), \(v\) 的情况同理

这个代码就更简单了

	ll merge(ll u , ll v){
		if(!u || ! v) return u + v; // 最终有一个节点为空，就返回不是空的
		if(tree[u].rnk < tree[v].rnk){ // 条件随意
			tree[u].rs = merge(tree[u].rs , v);
			pushup(u);
			return u;
		}else{
			tree[v].ls = merge(u , tree[v].ls);
			pushup(v);
			return v;
		}
	}

开始起飞

会了 \(split\) 与 \(merge\) , 那么就是会了 \(fhq-Treap\),目光看向模版题

现在可以利用 \(split\) 和 \(merge\) 把题目中的所有操作写出来。可以先想一想，然后在看下面的内容

插入节点

我要插入一个权值为 \(val\) 的节点，那么肯定得先分裂成两个部分 \([1,val]\) , \((val,n]\) , 然后将新生成的节点与 \([1,val]\) 合并

代码

	void insert(ll val){
		ll x , y;
		split(root , x , y , val);
		root = merge(merge(x , addnode(val)) , y);
	}

删除节点

删除节点有两种，一种是把所有的 \(val\) 全部删除，另一种就是将一个 \(val\) 的节点删除

对于前者，先 \(split\) 分成三部分 \([1,val-1] , (val - 1 , val] , (val , n]\) , 然后将 \([1,val-1]\) 与 \((val , n]\) 的部分合并
对于后者，也是 \(split\) 分成三部分,对于中间部分，由于全部都是 \(val\) , 只需要把根节点的左右节点合并就可以然后区间 \((val-1 , val]\) 的大小就减少了一位，然后在把三个全部合并即可

在本题里，删除操作是后者

    void del(ll val){
		ll x , y , z;
		split(root , x , y , val);
		split(x , x , z , val - 1);
		z = merge(tree[z].ls , tree[z].rs);
		root = merge(merge(x,z),y);
	}

查看 \(val\) 的排名

考虑分裂成为 \([1,val-1] ，(val-1,n]\) 两个区间，然后第一个区间的大小加一就是 \(val\) 的排名了

记得要合并

	ll getrnk(ll val){
		ll x , y;
		split(root , x , y , val - 1);
		ll res = tree[x].siz + 1;
		root = merge(x , y);
		return res;
	}

查看排名为 \(x\) 的大小 \(val\)

这一个部分就无法通过分裂与合并来完成了(~~如果可以可以在评论区留言~~)

我们知道对于一个二叉搜索树，它的中序遍历就是原来的序列排序后的结果。那么对于一个节点的排名就是它的左子树的大小加上 \(1\)（正常来说） , 即是自己。而 \(Treap\) 刚好具有这种性质于是直接从根开始遍历查找。

设当前遍历到的节点为 \(now\)

当 \(now.ls.siz + 1 == x\) 那么 \(now\) 就是答案
当 \(now.ls.siz + 1 > x\) , 那么答案在 \(now\) 的左子树， \(now \leftarrow now.ls\)
当以上两种情况都不是时，那么答案就在 \(now\) 的右子树，但是由于右子树的大小无法加上左子树的大小，因此要 \(x \leftarrow x - (now.ls.siz + 1)\) , 然后 \(now \leftarrow now.rs\)

代码

	ll getsort(ll siz){
		ll now = root;
		while(now){
			if(tree[tree[now].ls].siz + 1 == siz) break;
			if(tree[tree[now].ls].siz + 1 > siz) now = tree[now].ls;
			else{
				siz -= tree[tree[now].ls].siz + 1;
				now = tree[now].rs;
			}
		}
		return tree[now].val;
	}

前驱与后继

这两个操作都很像，这边只讲一下找前驱

将树分裂成 \([1,val-1],(val-1,n]\) , 由于 \(Treap\) 具有二叉搜索树的性质，\([1,val-1]\) 的最大值，\(val\) 的前驱一定在 \([1,val-1]\) 的最右边，不断的去找即可。

	ll getpre(ll val){
		ll x , y , now;
		split(root , x , y , val - 1);
		now = x;
		while(tree[now].rs) now = tree[now].rs;
		root = merge(x , y);
		return tree[now].val;
	}
	
	ll getsuf(ll val){
		ll x , y , now;
		split(root , x , y , val);
		now = y;
		while(tree[now].ls) now = tree[now].ls;
		root = merge(x , y);
		return tree[now].val;
	}

代码 && 小结

普通平衡树模版

完整代码

#include <bits/stdc++.h>

using namespace std;
using ll = long long;
using pii = pair<ll,ll>;

const ll kMaxN = 1e5 + 7;

struct node{
	ll val , rnk , ls , rs , siz;
};

struct fhq{
	node tree[kMaxN];
	ll cnt , root;
	
	ll addnode(ll val){
		tree[++cnt] = {val , rand() , 0 , 0 , 1};
		return cnt;
	}
	
	void pushup(ll p){
		tree[p].siz = tree[tree[p].ls].siz + tree[tree[p].rs].siz + 1;
	}
	
	void split(ll now , ll &x , ll &y , ll val){
		if(!now) { // 节点没了，肯定就不会执行下去了
			x = y = 0;
			return;
		}
		if(tree[now].val <= val){
			x = now;
			split(tree[now].rs , tree[now].rs , y , val);
		}else{
			y = now;
			split(tree[now].ls , x , tree[now].ls , val);
		}
		pushup(now);
	}
	
	ll merge(ll u , ll v){
		if(!u || ! v) return u + v; // 最终有一个节点为空，就返回不是空的
		if(tree[u].rnk < tree[v].rnk){
			tree[u].rs = merge(tree[u].rs , v);
			pushup(u);
			return u;
		}else{
			tree[v].ls = merge(u , tree[v].ls);
			pushup(v);
			return v;
		}
	}
	
	void insert(ll val){
		ll x , y;
		split(root , x , y , val);
		root = merge(merge(x , addnode(val)) , y);
	}
	
	void del(ll val){
		ll x , y , z;
		split(root , x , y , val);
		split(x , x , z , val - 1);
		z = merge(tree[z].ls , tree[z].rs);
		root = merge(merge(x,z),y);
	}
	
	ll getrnk(ll val){
		ll x , y;
		split(root , x , y , val - 1);
		ll res = tree[x].siz + 1;
		root = merge(x , y);
		return res;
	}
	
	ll getsort(ll siz){
		ll now = root;
		while(now){
			if(tree[tree[now].ls].siz + 1 == siz) break;
			if(tree[tree[now].ls].siz + 1 > siz) now = tree[now].ls;
			else{
				siz -= tree[tree[now].ls].siz + 1;
				now = tree[now].rs;
			}
		}
		return tree[now].val;
	}
	
	ll getpre(ll val){
		ll x , y , now;
		split(root , x , y , val - 1);
		now = x;
		while(tree[now].rs) now = tree[now].rs;
		root = merge(x , y);
		return tree[now].val;
	}
	
	ll getsuf(ll val){
		ll x , y , now;
		split(root , x , y , val);
		now = y;
		while(tree[now].ls) now = tree[now].ls;
		root = merge(x , y);
		return tree[now].val;
	}
}T;

ll n;

ll opt , x;

int main(){
	cin>>n;
	for(int i = 1 ; i <= n ; i++){
		cin>>opt>>x;
		if(opt == 1) T.insert(x);
		if(opt == 2) T.del(x);
		if(opt == 3) cout<<T.getrnk(x)<<"\n";
		if(opt == 4) cout<<T.getsort(x)<<"\n";
		if(opt == 5) cout<<T.getpre(x)<<"\n";
		if(opt == 6) cout<<T.getsuf(x)<<"\n";
	}
	return 0;
}

对于平衡树的一系列操作，我们可以发现:

~~分裂了一定要合并~~
对于值域为 \([val_1,val_2] ,val_1 \leq val_2\) 的数量，就是对于的树的大小
可以利用二叉搜索树的性质完成操作
。。。

维护区间操作的平衡树——文艺平衡树

~~谁想到文艺平衡树这个名字的~~

先想一想文艺平衡树为什么可以维护序列操作。

对于一颗 \(Treap\) ，它是具有二叉搜索树的性质的（~~我说了多少遍这句话~~）,因此它的中序遍历为一个序列的。于是我们可以实现 \(log\) 级别的插入与删除以及更多的操作。

那么我们先看文艺平衡树板子题

修改 \(split\) 操作的定义我的理解是将值域分裂改为定义域分裂，分裂成 \([1,siz] , (siz , n]\) 的两个序列。

然后是翻转操作。我们可以学习线段树的懒标记，给要翻转的节点打上一个标记然后在要用到时就 \(pushdown\) 。

\(pushdown\) 部分原理和lzaytag差不多

	void pushdown(ll p){
		if(tree[p].rev){
        	swap(tree[p].ls , tree[p].rs);
        	tree[tree[p].ls].rev ^= 1;
        	tree[tree[p].rs].rev ^= 1;
        	tree[p].rev = 0; 
    	}
	}

然后是爆改我们的 \(split\) 函数，类似我们前面找排名为 \(x\) 的值的操作，递归向右节点时要减去当前节点的左子树的大小加 \(1\) , 记得加上 \(pushdown\)

	void split(ll now , ll &x , ll &y , ll siz){
		if(!now){
			x = y = 0;
			return;
		}
		pushdown(now);
		if(tree[tree[now].ls].siz + 1 <= siz){
			x = now;
			split(tree[now].rs , tree[now].rs , y , siz - tree[tree[now].ls].siz - 1);
		}else{
			y = now;
			split(tree[now].ls , x , tree[now].ls , siz);
		}
		pushup(now);
	}

现在思考翻转操作，我们是要翻转 \((l,r)\) 区间，于是把区间分解成三个长度分别为 \(l-1 , r - l + 1 , n - r - 1\) 的区间，然后给中间区间打上一个标记即可

	void reverse(ll l , ll r){
		ll a , b , c;
		split(root , a , b , l - 1);
		split(b , b , c , r - l + 1);
		tree[b].rev ^= 1;
		root = merge(merge(a,b),c);
	}

输出部分就是正常的递归左儿子然后输出再递归右儿子

完整代码

#include <bits/stdc++.h>

using namespace std;
using ll = int;
using pii = pair<ll,ll>;

const ll kMaxN = 100007;

struct node{
	ll val , rnk , ls , rs , siz;
	bool rev;
};

struct fhq{
	node tree[kMaxN];
	ll cnt , root;
	
	ll addnode(ll val){
		tree[++cnt] = {val , rand() , 0 , 0 , 1 , 0};
		return cnt;
	}
	
	void pushup(ll p){
		tree[p].siz = tree[tree[p].ls].siz + tree[tree[p].rs].siz + 1;
	}
	
	void pushdown(ll p){
		if(tree[p].rev){
        	swap(tree[p].ls , tree[p].rs);
        	tree[tree[p].ls].rev ^= 1;
        	tree[tree[p].rs].rev ^= 1;
        	tree[p].rev = 0; 
    	}
	}
	
	void split(ll now , ll &x , ll &y , ll siz){
		if(!now){
			x = y = 0;
			return;
		}
		pushdown(now);
		if(tree[tree[now].ls].siz + 1 <= siz){
			x = now;
			split(tree[now].rs , tree[now].rs , y , siz - tree[tree[now].ls].siz - 1);
		}else{
			y = now;
			split(tree[now].ls , x , tree[now].ls , siz);
		}
		pushup(now);
	}
	
	ll merge(ll u , ll v){
		if(!u || !v) return u + v;
		if(tree[u].rnk < tree[v].rnk){
			pushdown(u);
			tree[u].rs = merge(tree[u].rs , v);
			pushup(u);
			return u;
		}else{
			pushdown(v);
			tree[v].ls = merge(u , tree[v].ls);
			pushup(v);
			return v;
		}
	}
	
	void reverse(ll l , ll r){
		ll a , b , c;
		split(root , a , b , l - 1);
		split(b , b , c , r - l + 1);
		tree[b].rev ^= 1;
		root = merge(merge(a,b),c);
	}
	
	void insert(ll val){
		ll a , b;
		split(root , a  , b , val - 1);
		root = merge(merge(a , addnode(val)) , b);
	}
	
	void dfs(ll pos){
    	if(pos == 0) return;
    	pushdown(pos);
    	dfs(tree[pos].ls);
    	cout<<tree[pos].val<<" ";
    	dfs(tree[pos].rs);
	}
}T;

ll n , m;

int main(){
	cin>>n>>m;
	for(int i = 1 ; i <= n ; i++){
		T.insert(i);
	}
	for(int i = 1 ; i <= m ; i++){
		ll l , r;
		cin>>l>>r;
		T.reverse(l,r);
	}
	T.dfs(T.root);
	return 0;
}

例题

~~本来还是不想放例题的~~
两道书架
P3850
P2596

posted @ 2025-12-07 20:43 reisa_awa 阅读(5) 评论(0) 收藏举报

刷新页面返回顶部

Loading

reisampt

fhq-Treap学习笔记

前言

啥是 fhq-treap

啥是 Treap

原理

\(fhq-Treap\)

基本结构

\(addnode\) 操作

\(pushup\) 操作

\(split\) 操作

\(merge\) 操作

开始起飞

插入节点

删除节点

查看 \(val\) 的排名

查看排名为 \(x\) 的大小 \(val\)

前驱与后继

代码 && 小结

维护区间操作的平衡树——文艺平衡树

完整代码

例题

公告