哈希表

哈希表的基本原理

哈希表是一个加强版的数组。数组可以通过索引在O（1）的时间复杂度内查找到对应元素，索引是非负整数；哈希表是类似的，可以通过key在O(1)的时间复杂度内查找到这个key对应的value，key的类型可以是数字、字符串等。

怎么做？

哈希表的底层就是一个数组（table），先把key通过一个哈希函数（hash）转换成数组里的索引，然后增删查改操作和数组相同：

package com.wang.base.hashTable;

public class Demo01 {
    //哈希表伪码逻辑
    class MyHashMap{
        private Object[]table;
        //增改，复杂度O(1)
        public void put(K key,V value){
            int index=hash(key);
            table[index]=value;
        }
        //查，复杂度O(1)
        public V get(K key){
            int index=hash(key);
            return table[index];
        }
        //删，复杂度O(1)
        public void remove(K key){
            int index=hash(key);
            table[index]=null;
        }
        //哈希函数，把key转换成table中的合法索引
        //复杂度必须是O(1)，才能保证上面方法的复杂度是O(1)
        private int hash(K key){
            //...
        }
    }
}

几个关键概念及原理

key是唯一的，value可以重复

类比数组，每个索引是唯一的，索引里面存的元素可以随便

key---》索引

value---》元素

哈希函数

哈希函数的作用是把任意长度的输入（key）转换成固定长度的输出（索引）

还要保证输入相同的key，输出也必须相同

那如何保证索引合法？

Java有个hashCode，可以返回int型，符合我们的要求，但是可能返回的是负数，但是索引是非负数，所以要想办法解决：

  int h=key.hashCode();
        /*
        位运算，把最高位的符号位去掉
        另外，位运算的运行速度比一般的算术运算快
         */
        h=h& 0x7fffffff;//这个0x7fffffff的二进制表达是0111 1111...1111，即除了最高位，其他都是1
    //把他和int进行&运算之后，最高位（符号位）会被清零，保证了h是非负数

还有一个问题，hashcode一般很大，需要把他映射成table数组的合法索引。

之前在环形数组里面用%来保证索引永远落在数组的合法范围内。所以这里也可以用%来保证索引的合法性

 int hash(Key key){
            int h=key.hashCode();
            //保证h为非负数
            h=h&0x7fffffff;
            //映射到table数组的合法索引
            return h%table.length;
        }

哈希冲突

当两个不同的key通过哈希函数得到相同的索引，怎么办呢？

哈希冲突是一定会有的，只能在算法层面妥善处理哈希冲突

有两种方法：

1. 拉链法：相当于是哈希表的底层数组不直接存储value类型，而是存储一个链表，当有不同key映射到同一索引上，这些key--》value对儿就存储在这个链表中

2. 线性探查法：一个key发现算出来的index值已经被别的key占了，就去index+1的位置看看，如果还是被占了，就继续往后找，直到找到一个空的位置为止

扩容和负载因子

拉链法和线性探查法虽然能解决哈希冲突，但是会导致性能下降。

拉链法的时间复杂度是O(K)，k是链表的长度

线性探查法的时间复杂度是O(k)，k是连续探查的次数

所以如果频繁出现哈希冲突，k会变大，导致哈希表的性能下降，这是我们想避免的

为什么会频繁出现哈希冲突？

1. 哈希函数设计的不好（大佬已解决）
2. 哈希表里装了太多key-value对了

所以出现“负载因子”这个概念，来解决第二点

负载因子是一个哈希表装满的程度的度量。一般来说，负载因子越大，说明哈希表里存储的key-value对子越多，越容易起哈希冲突

计算公式：size/table.length，其中size是key-value对的数量，table.length是哈希表底层数组的容量

当哈希表内元素达到负载因子时，哈希表会扩容。把分母变大，然后把旧数据转移进新数组

为什么不能依赖哈希表的遍历顺序

编程常识：哈希表中键的遍历顺序是无序的，不能依赖他的遍历顺序来编写程序。

这是为什么呢？

哈希表的遍历本质上是遍历那个底层数组：

 //遍历所有key的伪码逻辑
        
        //哈希表底层的table数组
        KVNode[]table=new KVNode[1000];
        //获取哈希表中所有键
        //我们不能依赖这个keys列表的顺序
        List<KeyType>keys=new ArrayList<>();
        for (int i = 0; i < table.length; i++) 
        {
         KVNode node=table[i];
         if (node!=null){
             keys.add(node.key);
         }
        }

首先，由于 hash 函数要把你的 key 进行映射，所以 key 在底层 table 数组中的分布是随机的，不像数组/链表结构那样有个明确的元素顺序。

其次，刚才讲了哈希表达到负载因子时会怎样？会扩容对吧，也就是 table.length 会变化，且会搬移元素。

那么这个搬移数据的过程，是不是要用 hash 函数重新计算 key 的哈希值，然后放到新的 table 数组中？

而这个 hash 函数，它计算出的值依赖 table.length。也就是说，哈希表自动扩容后，同一个 key 的哈希值可能变化，即这个 key-value 对儿存储在 table 的索引也变了，所以遍历结果的顺序就和之前不一样了。

你观察到的现象就是，这次遍历的第一个键是 key1，但是增删几个元素再遍历，可能发现 key1 跑到最后去了。

所以说，这些东西没必要背的，原理搞明白了，稍微推理下自己都能想通。

为什么不建议在 for 循环中增/删哈希表的 key

注意我这里说的是不建议，并不是一定不可以。因为不同的编程语言标准库对哈希表的实现不同，有些语言针对这种情况做了优化，所以到底行不行，要查阅文档。

我们这里仅从哈希表的原理上分析，在 for 循环中增/删哈希表的 key，是很容易出现问题的，原因和上面相同，还是扩缩容导致的哈希值变化。

遍历哈希表的 key，本质就是遍历哈希表底层的 table 数组，如果一边遍历一边增删元素，如果遍历到一半，插入/删除操作触发了扩缩容，整个 table 数组都变了，那么请问，接下来应该是什么行为？还有，在遍历过程中新插入/删除的元素，是否应该被遍历到？

扩缩容导致 key 顺序变化是哈希表的特有行为，但即便排除这个因素，任何其他数据结构，也都不建议在遍历的过程中同时进行增删，否则很容易导致非预期的行为。

如果你非要这样做，请确保查阅了相关文档，明确这个操作的行为是什么，做到心里有数。

key 必须是不可变的

只有那些不可变类型，才能作为哈希表的 key，这一点很重要。

所谓不可变类型，就是说这个对象一旦创建，它的值就不能再改变了。比如 Java 中的 String, Integer 等类型，一旦创建了这些对象，你就只能读取它的值，而不能再修改它的值了。

作为对比，Java 中的 ArrayList、LinkedList 这些对象，它们创建出来之后，可以往里面随意增删元素，所以它们是可变类型。

因此，你可以把 String 对象作为哈希表的 key，但不能把 ArrayList 对象作为哈希表的 key：

// 可以把不可变类型作为 key
Map<String, AnyOtherType> map1 = new HashMap<>();
Map<Integer, AnyOtherType> map2 = new HashMap<>();

// 不应该把可变类型作为 key
// 注意，这样写并不会产生语法错误，但是代码非常容易出 bug
Map<ArrayList<Integer>, AnyOtherType> map3 = new HashMap<>();

为啥不建议把可变类型作为 key 呢？就比如这个 ArrayList 吧，它的 hashCode 方法的实现逻辑如下：

public int hashCode() {
    for (int i = 0; i < elementData.length; i++) {
        h = 31 * h + elementData[i];
    }
}

第一个就是效率问题，每次计算 hashCode 都要遍历整个数组，复杂度是 O(N)O(N)，这样就会导致哈希表的增删查改操作的复杂度退化成 O(N)O(N)。

更严重的问题是，ArrayList 的 hashCode 是根据它里面的元素计算出来的，如果你往这个 ArrayList 里面增删元素，或者其中某个元素的 hashCode 值发生改变，那么这个 ArrayList 的 hashCode 返回值也会发生改变。

比方说，你现在用一个 ArrayList 类型的 arr 变量作为哈希表的 key 在哈希表中保存了对应的 value。但如果 arr 中的某个元素在程序的其他位置被修改了，那么 arr 的 hashCode 就会变化。此时你再用这个 arr 变量去哈希表中查询，发现找不到任何值了。

也就是说，你存入哈希表的 key-value 意外丢失了，这是非常非常严重的 bug，还会带来潜在的内存泄漏问题。

所以正确的做法是，使用不可变类型作为哈希表的 key，比方说用 String 类型作为 key。因为 Java 中的 String 对象一旦创建出来，它的值就不允许被改变，你就不会遇到上面的问题。

String 类型的 hashCode 方法也需要遍历所有字符，但是由于它的不可变性，这个值只要算出来一次，就可以缓存下来，不用每次都重新计算，所以 平均时间复杂度依然是 O(1)O(1)。

总结（模拟面试题）

上面的说明应该已经吧哈希表的底层原理全部串起来了，最后模拟几个面试问题来总结一下本文的内容：

1、为什么我们常说，哈希表的增删查改效率都是 O(1)*O*(1)？

因为哈希表底层就是操作一个数组，其主要的时间复杂度来自于哈希函数计算索引和哈希冲突。只要保证哈希函数的复杂度在 O(1)O(1)，且合理解决哈希冲突的问题，那么增删查改的复杂度就都是 O(1)O(1)。

2、哈希表的遍历顺序为什么会变化？

因为哈希表在达到负载因子时会扩容，这个扩容过程会导致哈希表底层的数组容量变化，哈希函数计算出来的索引也会变化，所以哈希表的遍历顺序也会变化。

3、哈希表的增删查改效率一定是 O(1)*O*(1) 吗？

不一定，正如前面分析的，只有哈希函数的复杂度是 O(1)O(1)，且合理解决哈希冲突的问题，才能保证增删查改的复杂度是 O(1)O(1)。

哈希冲突好解决，都是有标准答案的。关键是哈希函数的计算复杂度。如果使用了错误的 key 类型，比如前面用 ArrayList 作为 key 的例子，那么哈希表的复杂度就会退化成 O(N)O(N)。

4、为啥一定要用不可变类型作为哈希表的 key？

因为哈希表的主要操作都依赖于哈希函数计算出来的索引，如果 key 的哈希值会变化，会导致键值对意外丢失，产生严重的 bug。

用数组加强哈希表

添加randomKey（）API

现在我给你出个题，让你基于标准哈希表的 API 之上，再添加一个新的 randomKey() API，可以在 O(1)O(1) 的时间复杂度返回一个随机键：

interface Map<K,V>{
        //获取key对应的value，时间复杂度O(1)
        V get(K key);
        //添加/修改key-value对，时间复杂度O(1)
        void put(K key,V value);
        //删除key-value对，时间复杂度O(1)
        void remove(K key);
        //是否包含key，时间复杂度O(1)
        boolean containsKey(K key);
        //返回所有key，时间复杂度O(N)
        List<K>keys();
        //新增API:随机返回一个key，要求时间复杂度O(1)
        K randomKey;
    }

通过前面的学习，你应该知道哈希表的本质就是一个 table 数组，现在让你随机返回一个哈希表的键，很容易就会联想到在数组中随机获取一个元素。

在标准数组，随机获取一个元素很简单，只要用随机数生成器生成一个 [0, size) 的随机索引，就相当于找了一个随机元素：

int randomeElement(int[] arr) {
    Random r = new Random();
    // 生成 [0, arr.length) 的随机索引
    return arr[r.nextInt(arr.length)];
}

这个算法是正确的，它的复杂度是 O(1)，且每个元素被选中的概率都是 1/n，n 为 arr 数组的总元素个数。

但你注意，上面这个函数有个前提，就是数组中的元素是紧凑存储没有空洞的，比如 arr = [1, 2, 3, 4]，这样才能保证任意一个随机索引都对应一个有效的元素。

如果数组中有空洞就有问题了，比如 arr = [1, 2, null, 4]，其中 arr[2] = null 代表没有存储元素的空洞，那么如果你生成的随机数恰好是 2，请问你该怎么办？

也许你想说，可以向左或者向右线性查找，找到一个非空的元素返回，类似这样：

// 返回一个非空的随机元素（伪码）
int randomeElement(int[] arr) {
    Random r = new Random();
    // 生成 [0, arr.length) 的随机索引
    int i = r.nextInt(arr.length);
    while (arr[i] == null) {
        // 随机生成的索引 i 恰巧是空洞
        // 借助环形数组技巧向右进行探查
        // 直到找到一个非空元素
        i = (i + 1) % arr.length;
    }
    return arr[i];
}

这样是不行的，这个算法有两个问题：

1、有个循环，最坏时间复杂度上升到了 O(N)O(N)，不符合 O(1)O(1) 的要求。

2、这个算法不是均匀随机的，因为你的查找方向是固定的，空洞右侧的元素被选中的概率会更大。比如 arr = [1, 2, null, 4]，元素 1, 2, 4 被选中的概率分别是 1/4, 1/4, 2/4。

那也许还有个办法，一次运气不好，就多来随机几次，直到找到一个非空元素：

// 返回一个非空的随机元素（伪码）
int randomeElement(int[] arr) {
    Random r = new Random();
    // 生成 [0, arr.length) 的随机索引
    int i = r.nextInt(arr.length);
    while (arr[i] == null) {
        // 随机生成的索引 i 恰巧是空洞
        // 重新生成一个随机索引
        i = r.nextInt(arr.length);
    }
    return arr[i];
}

现在这个算法是均匀随机的，但问题也非常明显，它的时间复杂度竟然依赖随机数！肯定不是 O(1)O(1) 的，不符合要求。

怎么样，从一个带有空洞的数组中随机返回一个元素是不是都把你难住了？

别忘了，我们现在的目标是从哈希表中随机返回一个键，哈希表底层的 table 数组不仅包含空洞，情况还会更复杂一些：

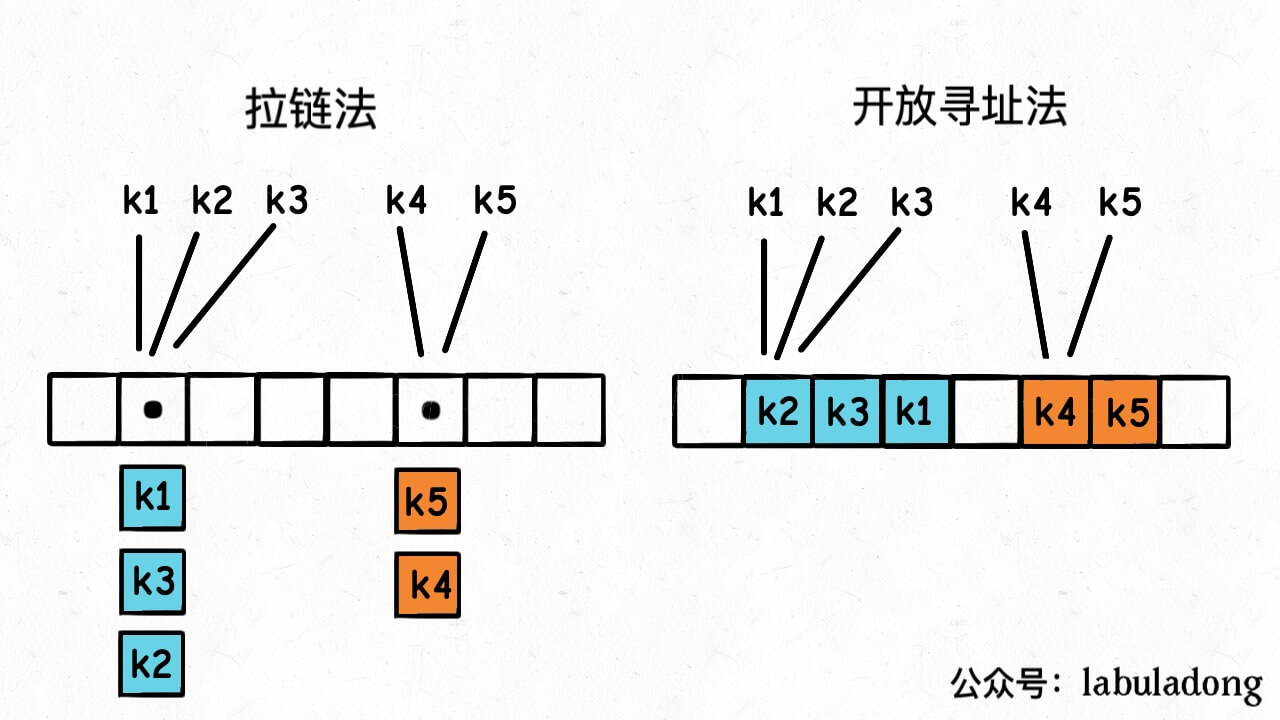
如果你的哈希表用开放寻址法解决哈希冲突，那还好，就是带空洞数组的场景。

如果你的哈希表用拉链法，那可麻烦了。数组里面的每个元素是一个链表，你光随机一个索引是不够的，还要随机链表中的一个节点。

而且注意概率，这个拉链法，就算你均匀随机到一个数组索引，又均匀随机该索引存储的链表节点，得到的这个键是均匀随机的么？

其实不是，上图中 k1, k2, k3 被随机到的概率是 1/2 * 1/3 = 1/6，而 k4, k5 被随机到的概率是 1/2 * 1/2 = 1/4，这不是均匀随机。

唯一的办法就是通过 keys 方法遍历整个 table 数组，把所有的键都存储到一个数组中，然后再随机返回一个键。但这样复杂度就是 O(N)O(N) 了，还是不符合要求。

是不是感觉已经走投无路了？所以说，还是要积累一些经典数据结构设计经验，如果面试笔试的时候遇到类似的问题，你现场想恐怕是很难的。下面我就来介绍一下如何用数组加强哈希表，轻松实现 randomKey() API。

哈希数组（ArrayHashMap）实现思路

其实我前面给你分析拉链法，就是故意误导你的。和链表加强哈希表一样，只要你陷入到细节里面，那肯定觉得很复杂。

所以说，不要陷入细节。那什么拉链法线性探查法，只是给你介绍下哈希表的运行原理，了解一下为啥它的复杂度是那样。

现在，以及未来做题的时候，你只要记住哈希表是一个能进行键值操作的数据结构，就行了，把它当成一个黑盒，不要去管它的底层实现。

紧凑的数组可以随机返回一个元素，现在我们想随机返回哈希表的一个键，那么最简单的方法就是这样：

// 伪码思路
class MyArrayHashMap {
    // arr 数组存储哈希表中所有的 key
    ArrayList<Integer> arr = new ArrayList<>();
    Map<Integer, Integer> map = new HashMap<>();

    // 添加/修改 key-value 对，时间复杂度 O(1)
    public void put(int key, int value) {
        if (!map.containsKey(key)) {
            // 新增的 key 加入到 arr 数组中
            arr.add(key);
        }
        map.put(key, value);
    }

    // 获取 key 对应的 value，时间复杂度 O(1)
    public int get(int key) {
        return map.get(key);
    }

    // 新增 API：随机返回一个 key，要求时间复杂度 O(1)
    public int randomKey() {
        Random r = new Random();
        // 生成 [0, arr.size()) 的随机索引
        return arr.get(r.nextInt(arr.size()));
    }

    // 删除 key-value 对，时间复杂度 O(1)
    public void remove(int key) {
        ...
    }
}

这个思路非常简单，就是用一个数组 arr 维护哈希表中所有的键，然后通过随机索引返回一个键。这样就能保证均匀随机，且时间复杂度是 O(1)O(1)。

但你注意，我没有实现哈希表的 remove 方法。因为这个方法不仅要删除哈希表 map 中的 key，还要删除 arr 数组中的元素 key，而删除数组中的元素时间复杂度是 O(N)O(N)，因为我们需要搬移数据以保持元素的连续性。

那么有没有办法让 arr 数组不用搬移数据，还能保持元素的连续性呢？

其实可以做到：你可以把待删除的元素，先交换到数组尾部，然后再删除，数组尾部删除元素的时间复杂度是 O(1)O(1)。

当然，这样的代价就是数组中的元素顺序会被打乱，但是对于我们当前的场景来说，数组中的元素顺序并不重要，所以打乱了也无所谓。

比如 arr = [1, 2, 3, 4, 5]，如果要删除 2，我先把 2 交换到数组尾部，变成 arr = [1, 5, 3, 4, 2]，然后只需花 O(1)O(1) 的时间即可删除尾部元素 2，且数组的连续性不会被破坏。

是不是思路一下就打开了？

但现在还有个问题，就是你如何快速知道一个元素在数组中对应的索引呢？正常来说，需要遍历数组，找到元素对应的索引，这样时间复杂度是 O(N)O(N)。

但是现在不是有哈希表么，键值映射是干啥的？不就是帮你优化这种需要傻乎乎遍历的场景的么？

也就是说，你可以在哈希表中建立数组元素和数组索引的映射关系，这样你就能在 O(1)O(1) 的时间复杂度内找到数组元素对应的索引了。

好了，讲到这里，整个思路已经比较清晰，下面直接看代码实现吧。

代码实现

package com.wang.base.hashTable;

import java.util.ArrayList;
import java.util.HashMap;
import java.util.Random;

public class MyArrayHashMap <K,V>{
    private static class Node<K,V>{
        K key;
        V val;
        Node(K key,V val){
            this.key=key;
            this.val=val;
        }
    }
    //存储key和key在arr中的索引
    private final HashMap<K,Integer>map=new HashMap<>();
    //真正存储key-value的数组
    private final ArrayList<Node<K,V>>arr=new ArrayList<>();
    private final Random r=new Random();
    public V get(K key){
        if (!map.containsKey(key)){
            return null;
        }
        //获取key在map中的索引
        int index= map.get(key);
        return arr.get(index).val;
    }
    public void put(K key,V val){
        if (containsKey(key)){
            //修改
            int i= map.get(key);
            Node<K,V>node=arr.get(i);
            node.val=val;
            return;
        }
        //新增
        arr.add(new Node<>(key, val));
        map.put(key, arr.size()-1);
    }
    public void remove(K key){
        if (!map.containsKey(key)){
            return;
        }
        int index= map.get(key);
        Node<K,V>node=arr.get(index);
        //1.最后一个元素e和第index个元素node交换位置
        Node<K,V>e=arr.get(arr.size()-1);
        arr.set(index,e);
        arr.set(arr.size()-1,node);
        //2.修改map中e。key对应的索引
        map.put(e.key,index);
        //3.在数组中删除最后一个元素
        arr.remove(arr.size()-1);
        //4.在map中删除node。key
        map.remove(node.key);
    }
    //随机弹出一个键
    public K radomKey(){
        int n=arr.size();
        int randomIndex=r.nextInt(n);
        return arr.get(randomIndex).key;
    }
    public boolean containsKey(K key){
        return map.containsKey(key);
    }
    public int size(){
        return map.size();
    }

    public static void main(String[] args) {
        MyArrayHashMap<Integer,Integer>map=new MyArrayHashMap<>();
        map.put(1,1);
        map.put(2,2);
        map.put(3,3);
        map.put(4,4);
        map.put(5,5);
        System.out.println(map.get(1));
        System.out.println(map.radomKey());
        map.remove(4);
        System.out.println(map.radomKey());
        System.out.println(map.radomKey());
    }
}

用链表加强哈希表

哈希链表（LinkedHashMap）实现思路

我们先明确一下问题。

标准哈希表的键是无序存储在底层的 table 数组中的：

你光看这个图，看不出来这些键是按什么顺序插入的，且一旦触发扩缩容，这键的位置又会改变。

我们现在希望在不改变哈希表增删查改复杂度的前提下，能够按照插入顺序来访问所有键，且不受扩缩容影响。

那么一个最直接的思路就是，我想办法把这些键值对都用类似链表节点的结构串联起来，持有一个头尾结点 head, taile 的引用，每次把新的键插入 table 数组时，同时把这个键插入链表的尾部。

这样一来，只要我从头结点 head 开始遍历链表，就能按照插入顺序访问所有键了：

我们可以清楚地看出，键的插入顺序是 k2, k4, k5, k3, k1。

现在我就是想让这个键值映射中的键按照插入顺序排列，怎么把哈希表和链表结合起来？

答案是这样：

假设键和值都是字符串类型，标准的哈希表是这样：

HashMap<String, String> map = new HashMap<>();

// 插入键值对
String key = "k1";
String value = "v1";

map.put(key, value);

而我们现在给哈希表的值类型套了一层双链表结构：

// 双链表节点
class Node {
    String key;
    String value;
    Node prev;
    Node next;

    Node(String key, String value) {
        this.key = key;
        this.value = value;
    }
}

HashMap<String, Node> map = new HashMap<>();

// 插入键值对
String key = "k1";
String value = "v1";

map.put(key, new Node(key, value));

// 这里做了简化，实际实现中还要操作新的链表节点加入链表

这样一来，就实现了哈希链表结构：

• 我们还是可以在 O(1)O(1) 的时间复杂度内通过键查找到对应的双链表节点，进而找到键对应的值。
• 我们可以在 O(1)O(1) 的时间复杂度内插入新的键值对。因为哈希表本身的插入操作时间复杂度是 O(1)O(1)，且双链表头尾的插入操作时间复杂度也是 O(1)O(1)。
• 我们可以在 O(1)O(1) 的时间复杂度内删除指定的键值对。因为哈希表本身的删除操作时间复杂度是 O(1)O(1)，删除给定双链表节点的操作时间复杂度也是 O(1)*O*(1)。
• 由于链表节点的顺序是插入顺序，那么只要从头结点开始遍历这个链表，就能按照插入顺序访问所有键。

也就是说，我们在不改变标准哈希表的基本操作复杂度的前提下，实现了按照插入顺序访问所有键的需求。

这里需要注意，双链表节点同时拥有前后驱指针，才可以做到 O(1)O(1) 时间复杂度的删除操作。单链表节点只有后驱指针，但没有前驱指针，做不到 O(1)O(1) 时间复杂度的删除操作。所以哈希链表的实现中，只能使用双链表。

代码实现

package com.wang.base.hashTable;

import java.util.ArrayList;
import java.util.HashMap;
import java.util.List;

public class MyArrayHashMap <K,V>{

    private static class Node<K,V>{
        K key;
        V val;
        Node(K key,V val){
            this.key=key;
            this.val=val;
        }
    }

   private final Node<K,V>head,tail;
    private final HashMap<K,Node<K,V>>map=new HashMap<>();
    public MyArrayHashMap(){
        head=new Node<>(null,null);
        tail=new Node<>(null,null);
        head.next=tail;
        tail.prev=head;
    }
    public V get(K key){
        Node<K,V>node=map.get(key);
        if (node!=null){
            return node.val;
        }
        return null;
    }
    public void put(K key,V val){
        //若为新插入的节点，则同时插入链表和map
        if (!map.containsKey(key)){
            Node<K,V>node=new Node<>(key, val);
            addLastNode(node);
            map.put(key,node);
            return;
        }
        //若存在，则替换之前的val
        map.get(key).val=val;
    }
    public void remove(K key){
        //若key本不存在，直接返回
        if (!map.containsKey(key)){
            return;
        }
        //若key存在，则需要同时在哈希表和链表中删除
        Node<K,V>node=map.get(key);
        map.remove(key);
        removeNode(node);
    }
    public boolean constainsKey(K key){
        return map.containsKey(key);
    }
    public List<K>keys(){
        List<K>keyList=new ArrayList<>();
        for (Node<K,V>p=head.next;p!=tail;p=p.next){
            keyList.add(p.key);
        }
        return keyList;
    }
    public int size(){
        return map.size();
    }
    private void addLastNode(Node<K,V>x){
        Node<K,V>temp=tail.prev;//temp<->tail
        
        //temp<-x->tail
        x.next=tail;
        x.prev=temp;
        
        //temp<->x<->tail
        temp.next=x;
        tail.prev=x;
    }
    private void removeNode(Node<K,V>x){
        //prev<->x<->next
        Node<K,V>prev=x.prev;
        Node<K,V>next=x.next;
        
        prev.next=next;
        next.prev=prev;
        
        x.next=x.prev=null;
    }
    public static void main(String[] args) {
        MyArrayHashMap<String,Integer>map=new MyArrayHashMap<>();
        map.put("a",1);
        map.put("b",2);
        map.put("c",3);
        map.put("d",4);
        map.put("e",5);
        System.out.println(map.keys());//[a,b,c,d,e]
        map.remove("c");
        System.out.println(map.keys());//[a,b,d,e]
    }
}