图论最短路算法笔记

1 图的基本操作

1.1 图的存储

• 邻接表：

g[N][N] = {};
...
memset(g, 0x3f, sizeof g);
g[u][v] = w;

• 链式前向星：

int head[N] = {};
memset(head, 0x3f, sizeof head); 
struct edge{
    int pre, to, val;
}EDGE[N];
inline void addedge(int u, int v, int w, int i){
    EDGE[i] = {v, w, head[u]};
    head[u] = i;
}

1.2 图的遍历

图的遍历是指从图中的任一顶点出发，对图中的所有顶点访问一次且只访问一次（访问一次，但不止用到一次）。 图的遍历操作和树的遍历操作功能相似。

2 最短路算法

图求最短路有算法：

• Floyd
• Dijkstra
• SPFA（死了）
• Bellman-Ford
• ...

2.1 Floyd

• 用途：求任意两个结点之间的最短路
• 复杂度：\(O(n^3)\)
• 适用：适用于任何图，不管有向无向，边权正负，但是最短路必须存在。

for(reg int k=1; k<=n; ++k)
    for(reg int i=1; i<=n; ++i)
        for(reg int j=1; j<=n; ++j)
            if(g[i][k] + g[k][j] < g[i][j])
                g[i][j] = g[i][k]+g[k][j];

以上：\(g\) 为邻接矩阵。

2.2 Dijkstra

定义

• 用途：单源最短路径
• 复杂度：\(O(n^2) \rightarrow O(nlogn)\)
• 适用：非负权图

将结点分成两个集合：已确定最短路长度的点集（记为 \(S\) 集合）的和未确定最短路长度的点集（记为 \(V-S\) 集合）。一开始所有的点都属于 \(V-S\) 集合。

然后重复这些操作：
从 \(T\) 集合中，选取一个最短路长度最小的结点，移到 \(S\) 集合中。
对那些刚刚被加入 \(S\) 集合的结点的所有出边执行松弛操作。
直到 \(T\) 集合为空，算法结束。

步骤

• 1 初始化：
  源点 \(u\)，dis[N]，book[N]。
  初始化 dis(s)=0，其他点的 \(dis\) 均为 \(+\infty\)。
  建立集合 \(S\) 与 \(V-S\)。刚开始，只有 \(u\) 在 \(S\) 中。

vector<edge> e[MAXN];
int dis[MAXN], book[MAXN];

• 2 找 dis[] 最小：
  开始，dis[n] 为 源点 \(u \rightarrow n\) 的特殊最短路。
  寻找 dis[n] 中最小的节点 \(t\)（可优化）。
  
  
• 3 加入集合 \(S\)
  加入集合 \(S\)，现在 \(S\) 表示为最短路的部分。
  
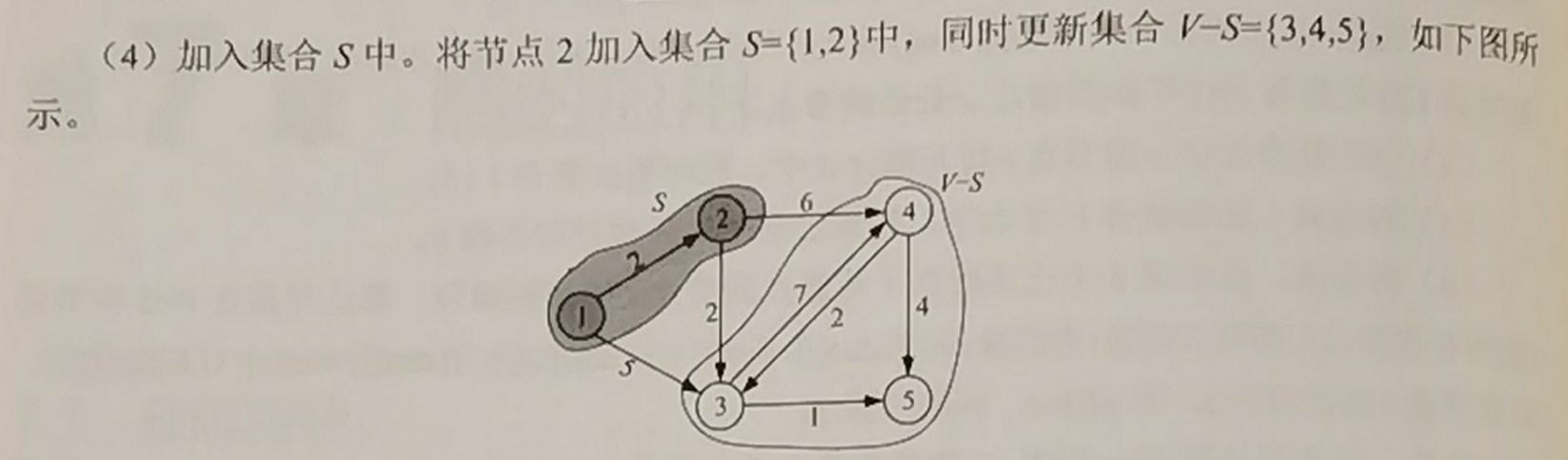
• 4 借东风
  与 Floyd 较为类似，就是以一个节点 \(i\) 作中转点，看看能不能将与周围的节点 \(k_1, k_2, ..., k_n\) 的边 \(k_1 \rightarrow i \rightarrow k_2\) 的长度减小（松弛）。
  
• 5 判结束
  如果 \(V-S\) 集合为空集，那么全部的 dis[] 都处理完毕，这时的 dis[n] 为 源点 \(u \rightarrow n\) 的最短路。
  

朴素算法（没写过，来自 oi-wiki）：

struct edge {
    int v, w;
};
vector<edge> e[MAXN];
int dis[MAXN], vis[MAXN];
void dijkstra(int n, int s) {
    memset(dis, 0x3f, (n + 1) * sizeof(int));
    dis[s] = 0;
    for (int i = 1; i <= n; i++) {
        int u = 0, mind = 0x3f3f3f3f;
        for (int j = 1; j <= n; j++)
            if (!vis[j] && dis[j] < mind)
                u = j, mind = dis[j];
        vis[u] = true;
        for (auto ed : e[u]) {
            int v = ed.v, w = ed.w;
            if (dis[v] > dis[u] + w) 
                dis[v] = dis[u] + w;
        }
    }
}

堆优化

堆优化就是用堆进行优化，而朴素的算法是“扫描”一遍图找最小的点。而小根堆优先队列优化就可以快速维护最小的点，大大减少时间复杂度（ \(O(nlogn)\) ）。

struct edge {
    int pre, to, val;
}EDGE[MAXN];
int dis[MAXN], book[MAXN], head[MAXN];

inline void addedge(int u, int v, int w, int i){
    EDGE[i] = {v, w, head[u]};
    head[u] = i;
}

inline void dijkstra(int s){
    memset(dis, inf, sizeof dis);
    priority_queue <pair<int, int>, vector<pair<int, int> >, greater<pair<int, int> > > heap;
    heap.push({0, s});
    while(!heap.empty()){
        int t = heap.top().second;
        heap.pop();
        if(book[t])
            continue;
        book[t] = true;
        for(reg int i=head[t]; i; i=EDGE[i].pre){
            if(dis[EDGE[i].to] > EDGE[i].val+dis[t]){
                dis[EDGE[i].to] = EDGE[i].to+dis[t];
                heap.push({dis[EDGE[i].to], EDGE[i].to});
            }
        }
    }
    return;
}

2.3 Bellman-Ford

定义

Bellman–Ford 算法是一种基于松弛操作的最短路算法，可以求出有负权的图的最短路，并可以对最短路不存在的情况进行判断。对于边 \((u,v)\)，松弛操作对应下面的式子：\(dis(v) = \min(dis(v), dis(u) + w(u, v))\)。算法本质就是不断尝试对图上每一条边进行松弛。我们每进行一轮循环，就对图上所有的边都尝试进行一次松弛操作，当一次循环中没有成功的松弛操作时，算法停止。

• 用途：单源最短路径
• 复杂度：\(O(nm)\)
• 适用：非负权图、负权图

2.3.1 SPFA（Bellman-Ford 算法队列优化）

定义

SPFA 算法是 Bellman-Ford 算法 的队列优化算法的别称，通常用于求含负权边的 单源最短路径，以及判负权环。 SPFA 最坏情况下时间复杂度和朴素 Bellman-Ford 相同，为 \(O (nm)\)。因为只有上一次被松弛的结点所连接的边才有可能引起下一次的松弛操作，所以就只用访问必要的边了。

• 用途：单源最短路径
• 复杂度：\(O(nm)\)
• 适用：非负权图、负权图

思想

用数组 \(dis\) 记录每个结点的目前最短值，用邻接表或邻接矩阵来存储图。
用队列用来保存待操作的结点。每次取出队首结点 \(u\)，并用 \(u\) 点当前最短路径对 \(u \rightarrow v\) 进行松弛操作，如果 \(v\) 点的当前最短路径有变化，并且 \(v\) 点不在队列中，就将 \(v\) 点放队尾。之后不断从队列中取出结点来松弛边，直至队列空为止，算法结束。

步骤

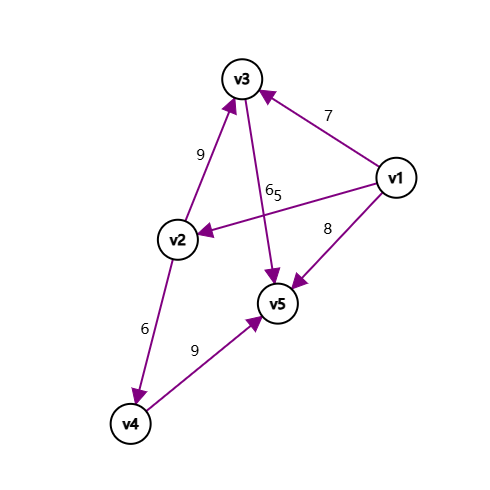
首先我们先初始化数组 \(dis\) 如下图所示：

\[[0, ∞, ∞, ∞, ∞] \]

队列 \(Q\) 为：\({v1}\)。

• 第一次循环：
  \(v1\) 出队，以 \(v1\) 松弛，发现 \(v1\) 到 \(v2, v3, v5\) 的最短路有变化，将 \(v2, v3, v5\) 加入 \(Q\)，更新 \(dis\)……

\[[0, 5, 7, ∞, 8] \]

队列 \(Q\) 为：\({v2, v3, v5}\)。

• 第二次循环：
  队头 \(v2\) 出队，以 \(v2\) 松弛，发现以 \(v2\) 松弛的 \(v4\) 的最短路有变化，将 \(v3, v4\) 加入 \(Q\)，更新 \(dis\)……

\[[0, 5, 7, 11, 8] \]

队列 \(Q\) 为：\({v3, v4, v5}\)。

• 第三次循环：
  队头 \(v3\) 出队，以 \(v3\) 松弛，发现以 \(v3\) 松弛的边没有变化，保持不变。

\[[0, 5, 7, 11, 8] \]

队列 \(Q\) 为：\({v4, v5}\)。

• 第四次循环：
  队头 \(v4\) 出队，以 \(v4\) 松弛，发现以 \(v4\) 松弛的边没有变化，保持不变。

\[[0, 5, 7, 11, 8] \]

队列 \(Q\) 为：\({v5}\)。

• 第五次循环：
  队头 \(v5\) 出队，以 \(v5\) 松弛，发现没有以 \(v5\) 松弛的边，保持不变。

\[[0, 5, 7, 11, 8] \]

队列 \(Q\) 为空。
算法结束。
所以 \(v1\) 到各个节点的距离是 \(0, 5, 7, 11, 8\)。

代码示例

struct edge {
    int v, w;
};

vector<edge> e[MAXN];
int dis[MAXN], cnt[MAXN], vis[MAXN];
queue<int> q;

bool spfa(int n, int s) {
    memset(dis, 0x3f, (n + 1) * sizeof(int));
    dis[s] = 0, vis[s] = 1;
    q.push(s);
    while (!q.empty()) {
        int u = q.front();
        q.pop(), vis[u] = 0;
        for (auto ed : e[u]) {
            int v = ed.v, w = ed.w;
            if (dis[v] > dis[u] + w) {
                dis[v] = dis[u] + w;
                cnt[v] = cnt[u] + 1;  
                if (cnt[v] >= n) return false;
                if (!vis[v])
                    q.push(v), vis[v] = 1;
            }
        }
    }
    return true;
}