st表

刷题单的时候刷到了st表，学了好久才学会，不过st表的模板题用线段树也能过不知道学来干嘛

其实st表还是有用的

建一颗线段树的时间复杂度是nlogn，建st表的时间复杂度也是nlogn，但是在查询区间最值的时候线段树的时间复杂度是logn而st表是O(1)要快一丁点。

要想实现st表我们首先需要一个二维数组st[i][j],其中i表示位置而j则表示i---2^j这个区间，那么我们就可以用st[i][j]存贮i---2^j这个区间的最值。

那么要如何来实现这样的一个功能呢，这里要用到一个小小的dp。

这样想我们把i---2^j这个区间从中间分成两个部分（这里借用马前卒大佬的图片）

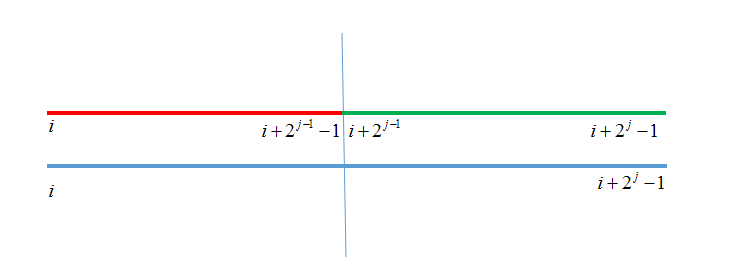
这样我们在枚举到st[i][j]这里的时候图片中分的区间（

st[i][j - 1]（左边的区间）

st[i + (1 << (j - 1))][j - 1]（右边的区间）

）其实已经枚举过了，那么我们只要取个最大值就可以了，像这样

for (int j = 1; j < 21; j++)
        for (int i = 1; i + (1 << j) - 1 <= n; i++)
            st[i][j] = max(st[i][j - 1], st[i + (1 << (j - 1))][j - 1]);

然后在查找区间的时候我们就可以覆盖式的查找也是把要查询的区间分成两个区间，像下面这个图这样

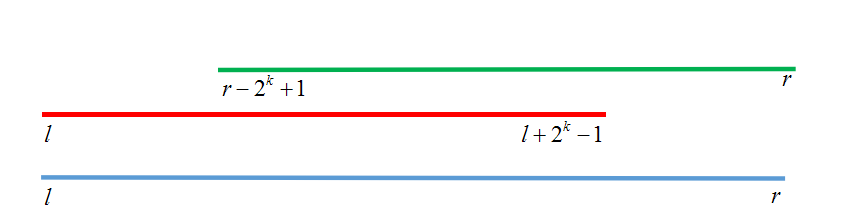
那么如何实现呢

可以把r-l+1取个log2即len=log2（r-l+1）那么st[l][len]代表的就是红色的线，然后我们再找左边的起点就是r-2^len+1

然后取两个区间的最值就好了

废话不多说上代码（不过这代码过不了版题）没加快读更好看

#include<iostream>
#include<algorithm>
#include<cmath>
#include<stdio.h>
using namespace std;
int st[1000005][21], maxx;
void find(int l, int r) {
    int len = log2(r - l + 1);
    maxx = max(st[l][len], st[r - (1 << len) + 1][len]);
    return;
}
int main() {
    int n, m;
    scanf("%d %d", &n, &m);
    for (int i = 1; i <= n; i++)
        cin >> st[i][0];
    for (int j = 1; j < 21; j++)
        for (int i = 1; i + (1 << j) - 1 <= n; i++)
            st[i][j] = max(st[i][j - 1], st[i + (1 << (j - 1))][j - 1]);
    for (int i = 1; i <= m; i++) {
        int l, r;
        cin >> l >> r;
        maxx = 0;
        find(l, r);
        printf("%d\n",maxx);
    }
    return 0;
}

太麻烦了，还是线段树好