OO_Unit1:面向对象设计与构造第一单元总结

面向对象设计与构造第一单元总结

目录

一、第一次作业总结

1.1 第一次作业基本思路

​ OO第一单元的需求是对一个具有形式化表述的表达式进行括号展开与化简，在第一次完成这一作业式，我仍然保留着面向过程的思维，虽然同样使用了递归下降的方法，但是对于表达式的层次结构还是利用了数据结构中的树来进行实现，而非使用面向对象中的继承父类或实现接口来实现，即以运算符作为分隔符，构建某一层的根结点与其左右子树。这一设计导致了程序中的类缺乏自治性，处理方法可以对几乎所有类中的数据进行更改，方法较为复杂和混乱。

​ 同时，对于数据维度的划分也没有考虑周全，表达式、因子均可以抽象为指数与系数对应的HashMap结构，但是我并没有将这个数据结构归属到表达式的类中，在解析时仍然按照字符串进行储存，导致了复杂度骤然上升。

​ 由于上述对于数据划分的失误，对于幂函数和括号乘积的化简就不得不通过复制子树的方式来实现，对于幂函数\(A^k\)是将其底数\(A\)所对应的子树复制\(k\)次，并用\(*\)运算符的节点连接起来，而对于括号乘积的化简则更是复杂，需要将左侧的括号表达式的克隆与右侧括号表达式的每一项用乘号连接后再将这些乘号用加号连接起来。这一处理并没有很好的利用抽象出来的数据结构，同时对于类的功能划分来说也没有体现表达式之间的层次关系。从设计来说是比较糟糕的，而我也为这一设计付出了相应的代价。

第一次作业的类图结构如下

可以看到，类与类之间并没有层次之间的关系，层次之间的关系仅在树结构中体现出来，各个类之间的关联更像业务流程之间的关联

建立一棵树(ExpressionResolver) -> 将树中的幂次进行转化(PowerCleaner) -> 将树中的乘法进行转化(TimeConverter) -> 通过树生成一颗多项式(Polynomial)

这是明显的面向过程的设计思路，在第一次作业中因为代码设计问题导致复杂度很高，在强测和互测中，复杂度带来的考虑不周产生的bug暴露了出来，这给我带来了很大的警醒。

1.2 第一次作业代码度量

1.2.1 代码体量分析

Class Total Lines Source Code Lines Source Code Lines Rate
ExpressionResolver.java 43 34 0.7906976744186046
ExpressionResolverFactory.java 211 180 0.8530805687203792
ExprPreProcessor.java 15 13 0.8666666666666667
MainClass.java 29 15 0.5172413793103449
Polynomial.java 173 154 0.8901734104046243
PowerCleaner.java 88 79 0.8977272727272727
Symbol.java 21 19 0.9047619047619048
TimeConverter.java 124 104 0.8387096774193549
TreeCopy.java 30 25 0.8333333333333334
TreeNode.java 126 101 0.8015873015873016

可以看到，位于主要流程中的类都有较大的代码行数，显得较为臃肿

1.2.2 方法复杂度(截取了复杂度较高的主要方法)

Method CogC ev(G) iv(G) v(G)
Polynomial.productTreeToPloy(TreeNode) 20.0 5.0 7.0 10.0
Polynomial.putAItem(boolean, Integer, StringBuilder) 53.0 4.0 17.0 17.0
Polynomial.toString() 8.0 2.0 6.0 6.0
PolynomialFactory.buildExprTree(String, boolean) 21.0 1.0 11.0 12.0
PolynomialFactory.convertExpr(TreeNode) 21.0 2.0 8.0 9.0
PolynomialFactory.convertNode(TreeNode) 25.0 1.0 13.0 15.0
PolynomialFactory.convertPower(TreeNode) 9.0 2.0 6.0 7.0
PolynomialFactory.exprProcess(String) 2.0 2.0 1.0 2.0
PolynomialFactory.externBracketCheck(String) 10.0 5.0 4.0 8.0
PolynomialFactory.getAPolynomial(String) 0.0 1.0 1.0 1.0
PolynomialFactory.plusCheck(String, TreeNode) 28.0 7.0 6.0 11.0
PolynomialFactory.plusSubValidCheck(String, int) 9.0 5.0 2.0 7.0
PolynomialFactory.powerCheck(String, TreeNode) 2.0 3.0 3.0 3.0
PolynomialFactory.timeCheck(String, TreeNode) 22.0 6.0 7.0 10.0
PolynomialFactory.timeConvert(TreeNode) 10.0 2.0 7.0 8.0
PolynomialFactory.treeRearrange(TreeNode) 9.0 2.0 8.0 9.0
TreeNode.checkPlusMinus() 4.0 1.0 4.0 5.0

​ 通过使用Metric Reloaded插件对方法进行复杂度分析，可以发现其主要方法中有很多复杂度指标都很高，接下来对各个复杂度指标的含义进行分析，首先明确各个指标代表什么方面

  • CogC ：Cognitive Complexity代表认知复杂度，其往往由以下因素导致，这一值愈高会导致对代码的认知变得愈困难

    • 代码中用到一些语法糖，把多句话缩为一句：代码不会变得更复杂；[1]
    • 出现"break"中止了线性的代码阅读理解，如出现循环、条件、try-catch、switch-case、一串的and or操作符、递归，以及jump to label：代码因此更复杂;[1:1]
    • 多层嵌套结构：代码因此更复杂；[1:2]

  • ev(G) ：Essential Complexity代表基本复杂度,基本复杂度是用来衡量程序非结构化程度的，非结构成分降低了程序的质量，增加了代码的维护难度，使程序难于理解。因此，基本复杂度高意味着非结构化程度高，难以模块化和维护。实际上，消除了一个错误有时会引起其他的错误。[2]

  • v(G) ：Cyclomatic Complexity代表圈复杂度，是用来衡量一个模块判定结构的复杂程度，数量上表现为独立路径的条数，即合理的预防错误所需测试的最少路径条数，圈复杂度大说明程序代码可能质量低且难于测试和维护，经验表明，程序的可能错误和高的圈复杂度有着很大关系。[2:1]

  • iv(G) ：Module Design Complexity代表模块复杂度，是用来衡量模块判定结构，即模块和其他模块的调用关系。软件模块设计复杂度高意味模块耦合度高，这将导致模块难于隔离、维护和复用。[2:2]

​ 观察我的方法复杂度统计结果，可以看到大部分主要方法的认知复杂度都较高，这给debug阶段的静态代码分析带来了困难，很容易就在某一个函数内卡住，导致了第一次作业的完成耗时较长而且debug过程也出现了漏网之鱼。再观察统计结果中的圈负责度，每一个方法的圈复杂度都较高，这些函数自身的测试就会出现很多需要测试的情况，而当他们叠加起来时，测试的覆盖会更加困难。同时函数的结构化程度也不佳，如putAItem函数，在循环结构中调用其他的函数形成递归结构，出现了多个出口，导致了程序的基础负责度较高，在对控制流进行分析时也难以达到较好的效果。

1.3 第一次作业Hack思路

​ 在第一次作业的互测时，仍然在使用数据轰炸的方法对互测房中的代码进行hack，这一方法在之前对自己代码的样例测试基础上进行改进的，但是实际上这一方式除了hack成功得到的分数以外，个人认为收获并不大，首先是因为对于数据轰炸而言，生成的数据并不是系统且完全的，其次在hack过程中，数据来源主要是灵光一现，实际上这一方式很难得到测试能力的提升。在之后的互测中，个人准备采用以下两种方法进行hack。

  1. 通过系统构造能对分支进行覆盖的测试集，对于这些测试集进行自动化测试
  2. 通过对代码进行静态/动态分析，从推理的角度来发现程序中的漏洞

1.4 第一次作业Bug修复策略

​ 在第一次作业中，出现的Bug并没有出现严重的结构性错误，而是由于代码复杂度较高导致的疏忽或笔误，所以仅需要将疏忽的地方进行修补即可。

二、第二次作业总结

2.1 第二次作业重构基本思路

本次作业的数据为一形式为一带三角函数形式项的多项式,输入基本形式与第一次作业相同，分为表达式、项、因子三个层级

  • 表达式为若干个项相加的结果
  • 项为若干个因子相乘的结果
  • 因子分为变量因子、常数因子、表达式因子
    • 变量因子：x的幂函数、三角函数(因子)、求和函数(因子）、自定义函数(因子）
    • 常数因子
    • 表达式因子

可以看出，因子是全局统一的一个基本属性，定义为一个接口(或是抽象类),由变量因子、常数因子、表达式因子将其继承，而变量因子又由上述四个因子将其继承，项则为单独的一个类，其只具备进行乘法运算的功能

根据

  • 表达式为0与若干个项相加的结果
  • 项为1与若干个因子相乘的结果

的逻辑结构，决定采用ArrayList的结构对项和因子的原始数据进行储存

对于一个表达式因子，其下含原始数据即为若干个项的数组(ArrayList)，对于一个项，其下含原始数据即为若干个因子的数组(ArrayList)

化简依赖的数据结构

本题要求将表达式进行化简，考虑表达式因子下属各项需要一个统一的数据结构进行表达以便于化简

即：表达式因子、项、下属各因子需要一个统一的、便于化简的数据结构进行储存与化简

由于项集合、各因子集合实际可以看作表达式的子集，所以考虑对于表达式进行统一的数据结构表示

  • 表达式为若干个项相加的结果

考虑从项入手，将项统一为

\[Poly \times \prod Circular \]

的形式

由作业1可知，多项式可以利用Hash相关的容器进行储存与表示，而对于\(\prod 三角函数因子\)

先将三角函数因子表示为

\[Circular(Factor)**PositiveNum \]

的形式,采用字符串Circular(Factor)i(代表\(Circular(Factor)^i\))的hashCode作为键进行储存，其中表达式因子的字符串必须是已通过本次程序统一的方法化简后的表达式字符串,i为不带符号的无前导零整数

本次作业的主要功能有两个

  1. 去除非必要的括号
  2. 对表达式进行合并化简

去除非必要的括号

由于表达式被拆分为了含有三角函数的项和不含三角函数的项，去掉括号后拆分出的表达式形式即为

\[\sum^i Coef \times x^i + \sum Coef\times x_i\times Circular(Factor)^j \]

拆分括号即为将每个项拆分为 \(Coef \times x^i\) 与 \(Coef\times x_i\times Circular(Factor)\) 之和的形式

表达式因子与项的数据表示是一致的，只是在进行计算时的运算方法不一样

而每个表达式因子的数据，即为其所有项之和的数据

每个项的数据，即为其下属所有因子的积的数据

每个自定义函数的数据，即为其下属表达式因子的数据

每个幂函数的数据，即为其下属因子的数据进行若干次积运算的数据

每个三角函数因子、常数因子的数据，即为其下属因子的数据

以上可以抽象出所有元素均具有一个getResult()方法，因子/项通过调用下属项/因子的getResult()方法得到统一的一组数据，并依照自己的方法对其进行合并，得到属于自己的getResult()方法的结果，最后回溯到根结点，得到属于输入到一整个表达式的结果。

且均需要用到数据之间的乘法与加法

根据以上的分析，对第二次作业的结构进行设计，得到第二次作业的因子结构如下

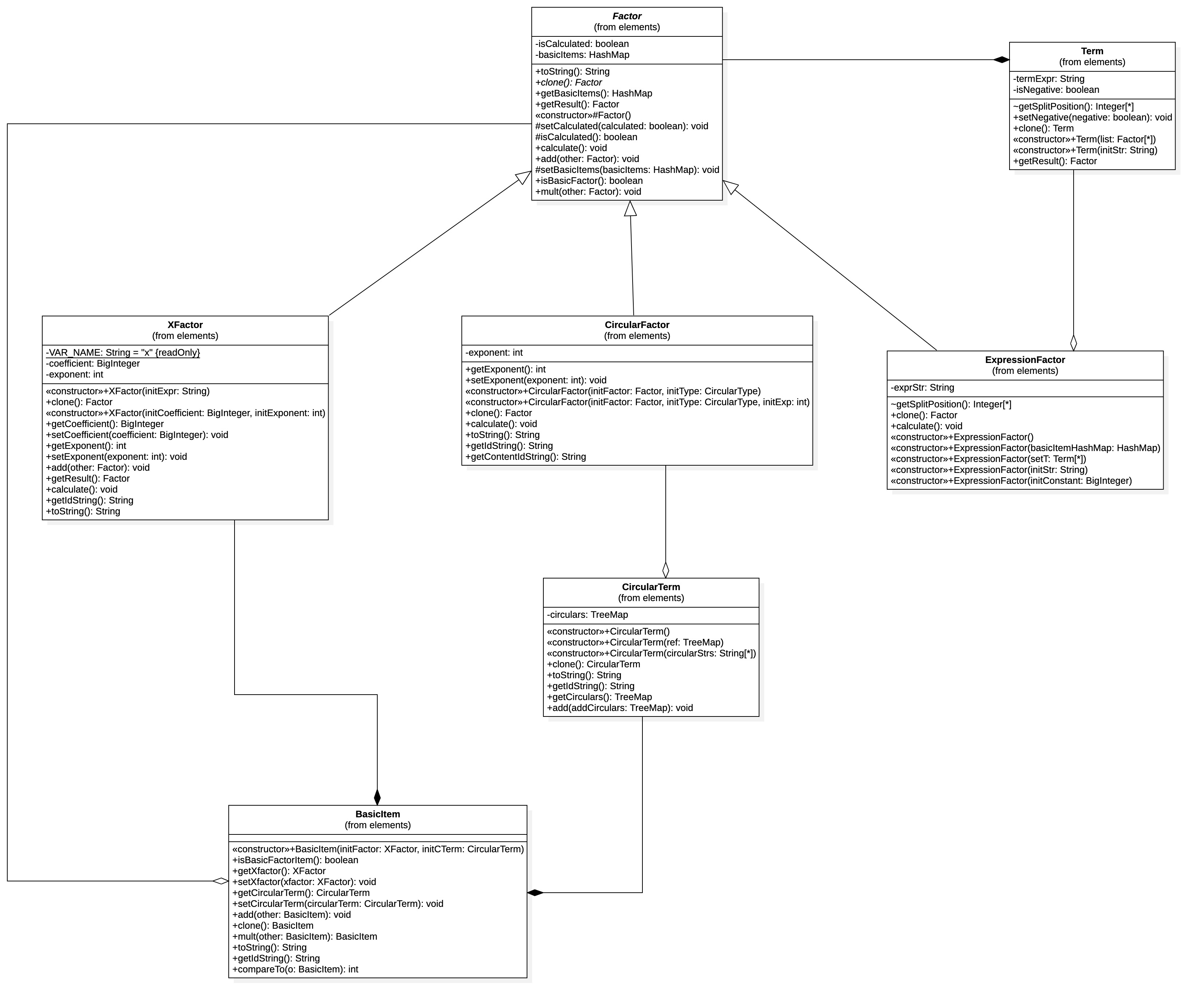
因子构造工厂设计

​ 由于各种因子具有统一的公共父类，可以采用工厂模式对其进行构造，此处对于因子设计了其工厂类FactorFactory类，并且考虑到求和函数、幂函数、自定义函数等特殊的因子类型，由为其设计了工厂类SumFactorFactory、ExponentFactorFactory、SelfDefinedFunctionFactory，并由FactorFactory`进行调用，此处在设计时存在一定的疏忽，应该采用抽象工厂的模式进行设计，使模块的内聚程度更高。

构造工厂的结构如下：

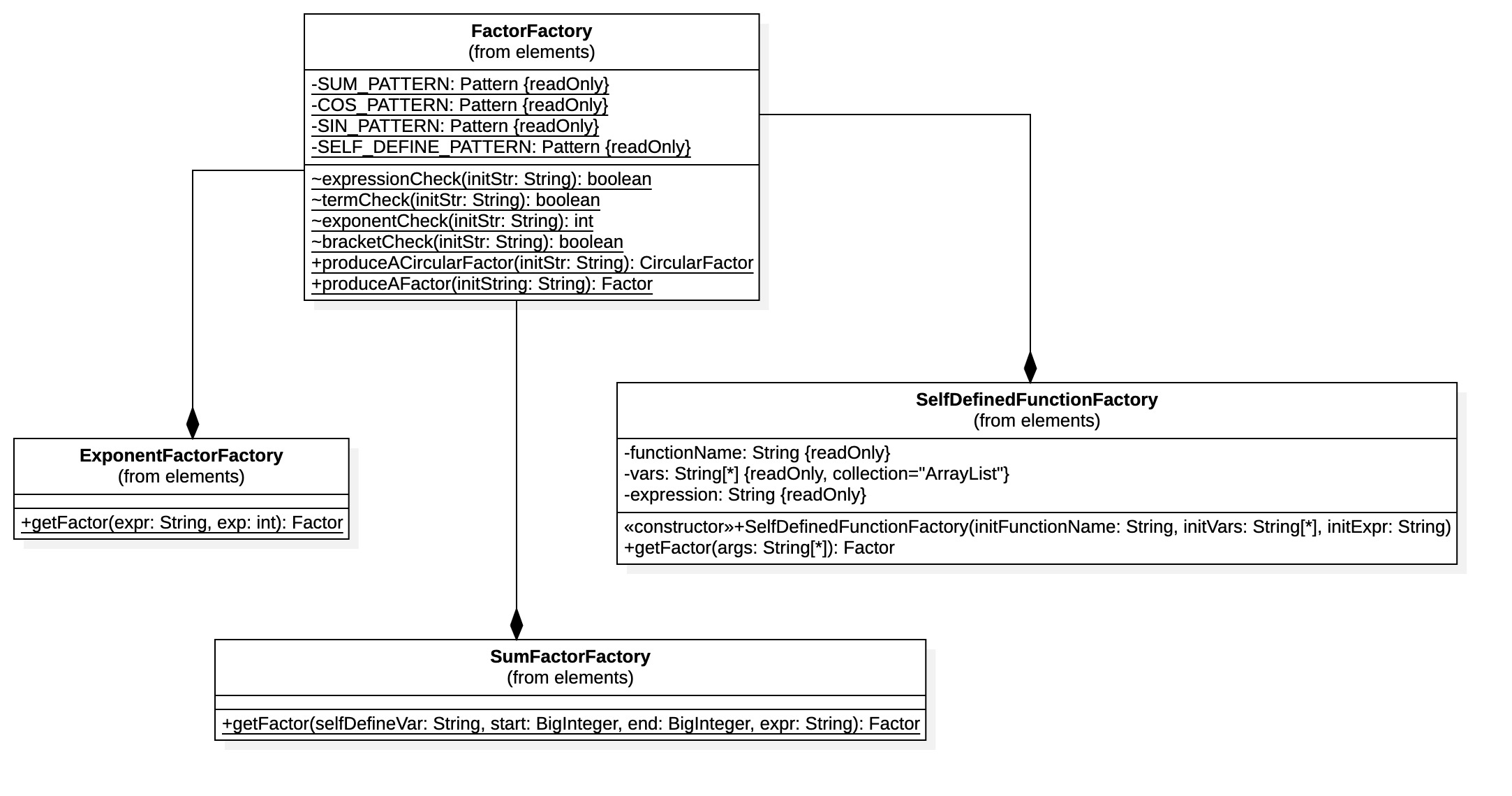
2.2 第二次作业代码度量

2.2.1 代码体量统计

Class Total Lines Source Code Lines Source Code Lines Rate
BasicItem.java 120 103 0.8583333333333333
CircularFactor.java 112 93 0.8303571428571429
CircularTerm.java 72 60 0.8333333333333334
CircularType.java 5 4 0.8
ExponentFactorFactory.java 16 12 0.75
ExpressionFactor.java 84 70 0.8333333333333334
ExpressionFormat.java 35 28 0.8
Factor.java 127 110 0.8661417322834646
FactorFactory.java 147 133 0.9047619047619048
MainClass.java 24 21 0.875
SelfDefinedFunctionFactory.java 30 24 0.8
SelfDefineFactoryArrange.java 39 33 0.8461538461538461
SumFactorFactory.java 27 21 0.7777777777777778
Term.java 81 71 0.8765432098765432
XFactor.java 112 95 0.8482142857142857

对比第一次的作业，主要的类虽然功能变复杂了，但是各类的代码行数却有相对的减少。同时，设计失误的FactorFactory类也能从中得到体现

2.2.2 代码复杂度分析

通过Mertric Reloaded工具对第二次作业的代码复杂度进行度量，发现构造的方法的复杂度得到了很有效的降低，但是由于produceAFactor()方法的设计失误，导致了在一个方法内部承担了多种因子的构造功能，使得这一函数的复杂度还是较高。除此之外，掺杂了优化方法的toString()方法也有较高的复杂度。在研讨课时有同学提出的构建方法与优化方法分离的提议还是十分有意义的一个想法。

本次设计中较高复杂度的方法如下(原数据中标红单元以加粗表示)：

method CogC ev(G) iv(G) v(G)
elements.CircularTerm.add(TreeMap) 4.0 1.0 3.0 3.0
elements.Factor.add(Factor) 4.0 1.0 3.0 3.0
elements.SelfDefineFactoryArrange.add(String) 4.0 1.0 3.0 3.0
elements.Term.Term(String) 4.0 1.0 4.0 4.0
elements.CircularFactor.calculate() 6.0 1.0 3.0 4.0
elements.FactorFactory.exponentCheck(String) 6.0 5.0 5.0 6.0
elements.FactorFactory.termCheck(String) 6.0 5.0 5.0 6.0
elements.Term.getSplitPosition() 6.0 1.0 6.0 6.0
elements.ExpressionFactor.getSplitPosition() 7.0 1.0 8.0 8.0
elements.Factor.mult(Factor) 7.0 1.0 5.0 5.0
elements.FactorFactory.expressionCheck(String) 7.0 5.0 6.0 7.0
elements.CircularFactor.toString() 14.0 3.0 6.0 8.0
elements.XFactor.toString() 14.0 2.0 9.0 9.0
elements.FactorFactory.produceAFactor(String) 17.0 9.0 11.0 11.0
elements.BasicItem.toString() 19.0 8.0 7.0 10.0
elements.Factor.toString() 23.0 2.0 9.0 9.0

三、第三次作业总结

3.1 第三次作业迭代思路

​ 第三次作业相较于第二次作业相比，接触了对于括号嵌套层数的限制，并且支持了更多种类的变量因子嵌套

​ 对于接触括号嵌套层数限制这一新需求，由于我在第二次作业时的设计就已经支持了多层的嵌套括号，所以这一部分并不需要进行修改。而对于更多种类的变量因子嵌套这一需求，由于要求三角函数中的表达式因子需要额外再加上一层括号，本来计划通过instance of 运算符判断Factor的类型后决定是否增加括号，但是这样处理无法识别可以化简为基本因子的表达式因子，于是粗糙地增加了一些特判条件。

​ 对于第三次作业的类与类之间的结构关系与第二次作业的一致，并没有进行什么修改。这次作业的轻松迭代，再次让我认识到了设计的重要性。

3.2 第三次作业代码度量

​ 第三次增加的方法中，有一个特判方法有较高的基础复杂度，是由于在if块中直接return造成的，其余的方法复杂度与第二次作业无异。

3.3 第三次作业Hack策略

第三次作业的互测中，我开始对系统性构造测试数据进行了尝试并用于测试自己的程序。

首先是针对各个因子

  • 变量因子
    • x的幂函数
      • 指数的大小(0,1,正常数字)
      • 指数的前导0情况
      • 指数是否带正号
    • 三角函数
      • 三角函数中的因子类型(五种情况)
      • 三角函数中的因子类型计算前计算后不一致的情况
    • 求和函数
      • 求和函数的上下限(下限小于上限、下限等于上限、下限大于上限)
      • 求和函数的上下限范围(负数+负数、负数+正数、正数+正数、超long范围数)
      • 求和函数的因子(带i，不带i)
      • 求和函数的因子类型(五种情况)
    • 自定义函数
      • 自定义函数的变量数目(1,2,3)
      • 自定义函数是否一定具有形参的字母
      • 自定义函数形参中\(x\)是否在第一个
      • 直接使用字符串替换后是否还满足形式化表述
  • 常数因子
    • 正数
    • 负数
    • 0
    • 超大数

在使用这一方法构造数据测试后，我成功测试出了房间中对求和函数上下限超long范围数无法处理的bug，但是同时也发现了一些问题

  1. 在构造测试数据时，我们往往会按照自己的思路来判断分支情况，如果面对的程序的思路不同、或者自身程序本来就没有考虑周全所有分支，那构造出来的测试数据就很有可能出现遗漏或疏忽
  2. 对于所有分支通过样例进行覆盖性测试，所需要的样例数是一个恐怖的数量级，同时也十分费时费力，应该能找到一种效率更高的手段来进行测试

四、单元总结与感想

​ 本次作业是我第一次尝试使用面向对象的方法去编写一个具有一定的实用功能的程序，在此次作业中，我一开始使用面向对象的思路去构建程序，导致了复杂度过高，出现了未发现的bug，意识到自己的架构问题后，参考课上实验、互测中优秀写法的架构思路，对自己的程序进行了重构，在第二第三次作业的强测和互测中均没有再被发现bug，同时，对比两次设计完成代码编写、debug困难程度等因素，也是后一次的设计优于前一次的设计。这一经历让我着实意识到了架构设计的重要性。

​ 不仅如此，一次次互测也在不断地向我强调测试的重要性，虽然暂时来看我还没有找到理想的测试方法，但是我仍然会在接下来三个单元里，不断寻找一个具有优秀表现的测试方法。

引用

  1. [工程质量] Cognitive Complexity 认知复杂度 https://www.jianshu.com/p/cd6da0a2fbcf ↩︎ ↩︎ ↩︎

  2. 软件复杂度-百度百科 https://baike.baidu.com/item/软件复杂度 ↩︎ ↩︎ ↩︎

posted @ 2022-03-25 21:01  鲁文澔  阅读(93)  评论(0)  编辑  收藏  举报