堆排序Go语言实现

堆排序是利用最大堆的性质将堆顶元素与数组末尾元素互换，然后重新将剩下的HeapSize-1部分的数组维护为最大堆的过程。

首先我们需要知道什么是堆，以及最大堆和最小堆等。

堆是数组，可以被看做是一颗完全二叉树(即任意两个叶子节点的深度相差不超过1且其排列与满二叉树契合)，反过来我们也可以说堆是一个完全二叉树的线性表达(即层次遍历的结果)。

我们可以从堆的二叉树视图得到堆的一些性质(我们预定义数组下标从1开始)：

• 对于数组任意下标i，其父节点下标为floor(i/2)，其左右子节点下标分别为2i,2i+1
• 高度为h的堆(叶节点高度为0)，其最大和最小的元素个数分别为：2^(h+1) - 1，2^h
• 每一层的元素在数组内都是连续的
• 对于元素总数为n的堆，第floor(n/2)个元素之后的都是叶子节点，简易证明如下：

1.下标为i的节点其左右子节点分别为2i,2i+1
2.当i的左右子节点都不存在时,i为叶子节点
3.即：2i > n && 2i+1 > n，等价于2i > n，因为i,n都是整数所以等价于：i > floor(n/2)
4.因此可以得到floor(n/2) + 1及其之后的元素皆为叶子节点

在知晓上述堆的性质之后，我们再来了解两种特殊的堆：最大堆和最小堆

其定义为：

最大堆是指所有节点均满足Array[Parent(i)] >= Array[i]，最小堆是指所有节点均满足Array[Parent(i)] <= Array[i]，当然根节点因为没有父节点所以不用讨论。

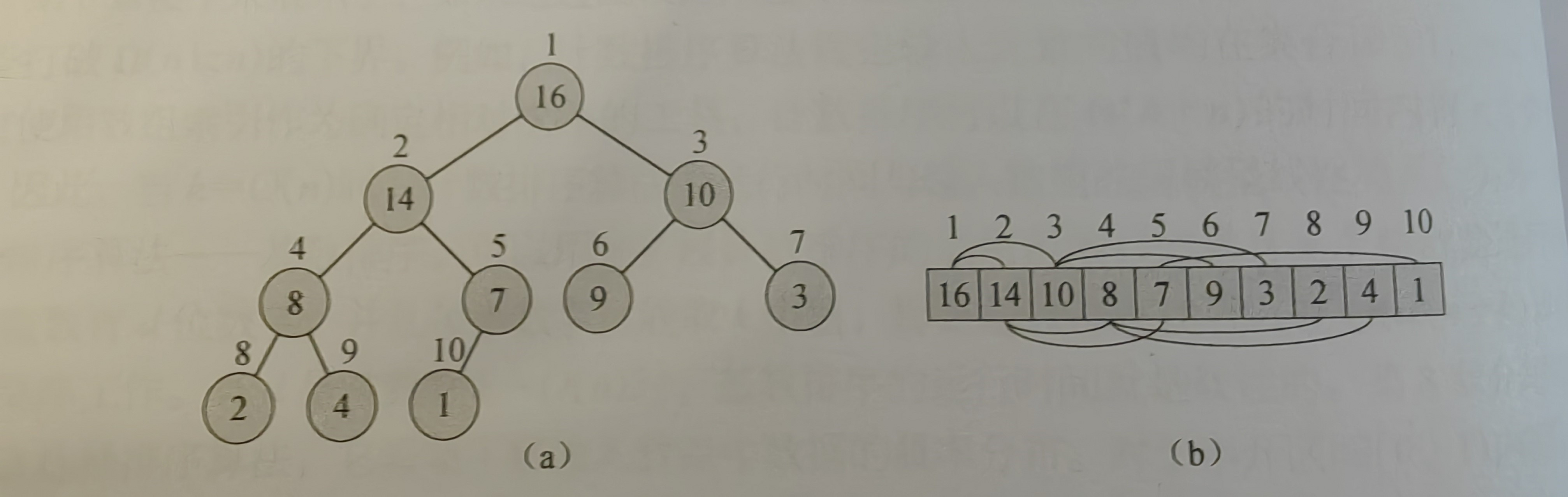
上述即为最大堆，右侧为原始数组表示。

可以看到最大堆子节点的值一定<=父节点，至于左右子节点的排序则无要求。

在堆排序算法中我们使用的是最大堆，最小堆一般用于构造优先队列，关于最小堆的应用可以查看《算法导论》中堆排序算法的优先队列一节。

堆排序算法：

从我们对堆排序算法的开篇解释来看，为了实现堆排序我们需要做如下操作：

1.将给定的数组构造为最大堆(因为原始数组顺序随机)，我们将函数命名为BuildMaxHeap

2.将堆顶元素与数组末尾互换后，剩余部分重新成为非最大堆，我们要将其维护为最大堆，这个函数命名为MaxHeapify（实际上这个函数在BuildMaxHeap中也要用到）

3.HeapSort主函数，即调用BuildMaxHeap构造最大堆，然后堆顶与末尾元素互换，移除末尾元素(通过将数组切片实现)后将数组剩下的部分重新最大堆化(MaxHeapify)，重复此过程直到堆元素个数为1

其代码如下(在最初为了方便解释我们使用了从1开始的下标，编码时使用原始下标更便捷，因此注意这里的转换)：

// MaxHeapify 将数组的第i个元素的子树构造为最大堆(假设其左右子树原本是最大堆)
func MaxHeapify(array []int, i int) {
	leftIndex := (i+1)*2 - 1
	rightIndex := (i + 1) * 2
	maxIndex := i
	if leftIndex <= len(array)-1 && array[leftIndex] > array[maxIndex] {
		maxIndex = leftIndex
	}
	if rightIndex <= len(array)-1 && array[rightIndex] > array[maxIndex] {
		maxIndex = rightIndex
	}
	if maxIndex != i {
		array[maxIndex], array[i] = array[i], array[maxIndex]
		// 交换过后的子堆不再满足最大堆性质(因为子堆顶被换成了较小值)，因此需要从原来的MaxIndex处递归下去
		MaxHeapify(array, maxIndex)
	}
}

// BuildMaxHeap 数组下标floor(n/2)-1之后的元素皆为叶子节点，利用此特性从下往上的构造最大堆
// 叶子节点没有子节点所以一定是最大堆，因此我们只要据此遍历所有的非叶节点即可，像插入排序那样倒序处理分片数组即可实现此目的
func BuildMaxHeap(array []int) {
	heapSize := len(array)
	for i := int(math.Floor(float64(heapSize/2))) - 1; i >= 0; i-- {
		MaxHeapify(array, i)
	}
}

func HeapSort(array []int) []int {
	n := len(array)
	BuildMaxHeap(array)
	for i := n - 1; i >= 1; i-- {
		array[i], array[0] = array[0], array[i]
		// 在交换首尾元素之后，新堆array[:n-1]不再是最大堆，但是根节点的子树未变还是最大堆
		// 我们使用MaxHeapify从下标0开始递归
		MaxHeapify(array[:i], 0)
	}
	return array
}

MaxHeapify的时间复杂度显然为O(logn)，因此BuildMaxHeap和HeapSort的时间复杂度皆为O(n*logn)，因此我们可以说堆排序算法的时间复杂度就是O(n*logn)。

下图为堆排序算法的图示，篇幅所限后边还有几幅没截，但我们只需要看a->b的过程即可通识其变化，a图通过如下操作变为了b:

1.首先a是构造好的最大堆，我们先交换了首尾元素，然后把末尾元素剔除(即新数组右边界左移一位)

2.然后元素1到了堆顶，因为以1为父节点的子树不是最大堆，但以14和10为父节点的子树还是最大堆，因此MaxHeapify会把堆顶元素1不断地下沉到他该在的位置，1先和14交换位置，然后和8交换位置，最后和4交换位置，最终1被放在了原本元素4的位置

3.之后我们继续剔除堆顶的14，递归下去直到当前要处理的数组大小为1(即array[:1])，此时整个array已经是有序的，返回即可。

整个流程其实就是不断地从堆顶摘出当前最大值，并维护最大堆的过程，其思想与选择排序相似，只不过相比于选择排序的线性查找最大值，堆排序利用二叉树实现了快速分层查找。