CSP2013-12-4 有趣的数

CSP2013-12-4 有趣的数

问题描述

我们把一个数称为有趣的，当且仅当：

　　1. 它的数字只包含0, 1, 2, 3，且这四个数字都出现过至少一次。
　　2. 所有的0都出现在所有的1之前，而所有的2都出现在所有的3之前。
　　3. 最高位数字不为0。

因此，符合我们定义的最小的有趣的数是2013。除此以外，4位的有趣的数还有两个：2031和2301。
请计算恰好有n位的有趣的数的个数。由于答案可能非常大，只需要输出答案除以1000000007的余数。

输入格式

　　输入只有一行，包括恰好一个正整数n (4 ≤ n ≤ 1000)。

输出格式

　　输出只有一行，包括恰好n 位的整数中有趣的数的个数除以1000000007的余数。

样例输入

4

样例输出

3

Solution

ps：今天被打击到了，下定决心开始刷csp真题，没想到csp以前还会考组合数学,orz

首先分析一下，题目中给出了三条限制关系

0 必须在所有的 1 之前，2 必须在所有的 3 之前，最高位不能为 0

那么由这三条可以确定我们的最高位填的一定是 2

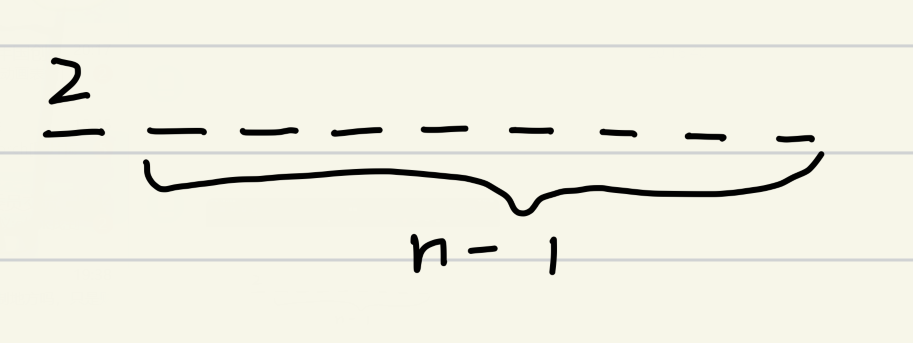
那么考虑剩下 \(n - 1\) 个位置

我们设 \(k\)为\(0\)和\(1\)两个数字出现的总次数，即我们把\(n-1\)个位置分配给 0 和 1 的方案数是 \(C_{n-1}^k\)

由于每个数字必须出现一次，即\(k\)的下界为2，同理 2 3 也至少得出现一次，因此上界为 \(n-2\)

再来考虑 0 和 1 的如何排列,题目要求 0 必须出现在所有的 1 之前,那么直接使用捆绑法,把所有的 0 看成 1 个数,那么只需要确定有多少个 0 ,剩下的就都是 1 了

因为 0 和 1 都至少得出现一次,且 0 和 1 的总个数为 \(k\),那么 0 的个数的范围为\([1,k-1]\)

因为顺序已定，只要确定了个数那么即可知道方案数,那么在确定\(k\)的情况下, 0 和 1 的组合排列方案数为\(k-1\)

同理，给定\(k\)的情况下，剩下\(n-1\)个位置中，2 和 3 的个数为\(n-k-1\)个，那么 2 和 3 的排列方案数为 \(n-k-1\)

即总方案数为

\(C_{n-1}^k\times(k-1)\times(n-k-1),k∈[2,n-2]\)

\(tips:\)题目要求取模运算，这当中又涉及到了组合数当中的\(\C_n^m\frac{n!}{(m!)\times(n-m)!}\)公式，我们知道涉及到除法的式子是不能直接取模的，因此需要计算对应的数的逆元，对逆元不太熟悉的读者可以看一下这篇博客

Code

#include<bits/stdc++.h>
#define lol long long
using namespace std;
const lol N = 1e3 + 10, mod = 1e9 + 7;
lol sum[N] = {1}, inv[N] = {1, 1};
lol n, ans = 0;
lol qpow(lol a, lol x, lol tot = 1ll) {
	while (x) {
		if (x & 1) tot = tot * a % mod;
		x >>= 1;
		a = a * a % mod;
	}
	return tot;
}
void init() {
	for (lol i = 1; i <= n; i++) sum[i] = sum[i - 1] * i % mod;
	for (lol i = 1; i <= n; i++) inv[i] = qpow(sum[i], mod - 2);
}
lol C(lol n, lol m) {
	return sum[n] * inv[m] % mod * inv[n - m] % mod;
}
int main() {
	cin >> n;
	init();
	for (lol k = 2; k <= n - 2; k++) {
		(ans += C(n - 1, k) * (k - 1) % mod * (n - k - 1) % mod) %= mod;
	}
	cout << ans << endl;
}