一道面积题的多种解法及多重拓展分析

原题：如下图，点O为正三角形ABC的中心，点M在AB上，点N在AC上，连接MN，交OB和OC分别于点P和点Q。已知MP=PQ=QN，AM=2BM，三角形OPQ的面积为1。求三角形ABC的面积。

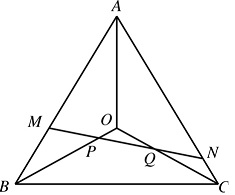
分析：本题的信息比较多，既有正三角形本身的特性，又有另外给出的线段比例关系。如何充分利用这些信息是解题的关键。

解法一：连接MO并延长交AC于点E，过点N作ME的平行线分别交AB和OB于点F和点H，如下图所示：

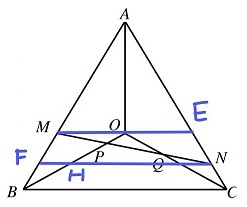
由AM=2BM以及正三角形的特性，可知ME//BC。

考察三角形MOP和NHP，由题设知PN=2PM，从而可知HN=2MO=ME，即MENH为平行四边形，进而易知MFH为正三角形，另外由正三角形特性易知FB=FH，于是MF=FB，即FN到上下两条平行线是等距的。

设MO为b，点P到MO的距离为h，由题设知三角形MOP的面积为bh/2=1，即bh=2。

由前述的三角形MOP和NHP的关系易知，ME到FN的距离为h+2h=3h，于是正三角形ABC的高为3h·6=18h。而AB=3BM=3MO=3b，于是三角形ABC的面积为3b·18h/2=3·18·2/2=54。

解法二（由walls老师的解法演变而来）：

连接MO、AQ和BQ，如下图所示：

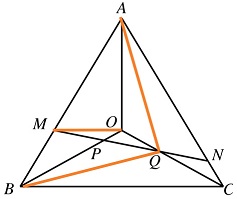
设三角形MBP的面积为x，由题设易知三角形MOB的面积为x+1，再由AM=2BM，可知三角形AOB的面积为3(x+1)。

由题设易知三角形BOQ的面积为x+1，由对称性知三角形AOQ的面积也为x+1。于是三角形ABQ的面积为5(x+1)。

另一方面，由题设易知三角形ABQ的面积为三角形BMQ的面积的3倍，即2x*3=6x。于是有5(x+1)=6x，解得x=5。所以三角形ABC的面积为3(5+1)·3=54。

walls老师的解法是利用三角形BOQ和AOQ面积相等列出方程，前者为x+1，后者用三角形AMQ减去三角形AMO和OMQ，即4x-2(x+1)-2。因此这里的解法二本质上还是walls老师的解法。

葛永超老师提供了另一个直接求法。具体如下：

解法三：

如上图所示，延长CO交AB于点D，过点M作DO的平行线交OB于点E。

由MP=PQ易知，三角形MEP和三角形QOP全等，于是OE=2PE。

再由三角形BME和三角形BDO相似可知，BM:BD=BE:BO，即AB/3:AB/2=2:3=BE:(BE+2PE)，得到BE=4PE。

于是三角形BME的面积为1·4=4。由上述的相似性知，三角形BDO的面积为4·(3/2)·(3/2)=9。于是由对称性知三角形ABC的面积为9·6=54。

walls老师在课堂上带着一个学生一起又找到了一种直接求法，具体如下：

解法四：

图中点D是CO的延长线与AB的交点，由对称性易知点D是AB的中点。由风筝（燕尾）模型知三角形AOQ的面积与三角形MOQ的面积之比为AD:DM=AD:(BD-BM)=3:(3-2)=3:1。由题设易知三角形MOQ的面积为2，于是三角形AOQ的面积为2·3=6。

另外，易知三角形BMO的面积等于三角形BOQ的面积，即为6，进而推出三角形AOM的面积为6·2=12。于是三角形ABC的面积为(6+12)·3=54。

这个解法直接沟通了walls老师此前的解法：x+1=6。

 

 葛老师进一步指出原题里只需给出MP=PQ即可，而无需再给出PQ=QN。这实际上衍生出如下的两个新题。

 

拓展题1：在原题的基础上去除不必需的条件PQ=QN（如下图所示，QN线段已经被抹除了），其余和原题一样。

 

在这里，原题的上述几种解法中，只有解法一需要做调整。具体如下：

连接MO，过点Q作MO的平行线分别交OB于点D，如下图所示：

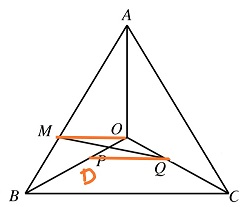
由AM=2BM以及正三角形特性可知，MO//BC。由MP=PQ知，三角形MOP与三角形QDP全等，于是MO=DQ，OP=DP，三角形ODQ的面积为三角形OPQ的面积的2倍，即1*2=2。

另由MO//BC知，角MBO=角MOB，MBO为等腰三角形，MB=MO。

综上可知，BC=3DQ。再由三角形ODQ与三角形OBC相似可知，三角形OBC的面积为2*3*3=18。于是三角形ABC的面积为18*3=54。

 

拓展题2：在原题的图中仅给出MP=PQ，求证：PQ=QN。

证法一：连接MO并延长交AC于点E，分别由点Q和点N做ME的垂线，垂足分别为点D和点G，过点Q作BC的平行线交OB于点F，连接QE，如下图所示：

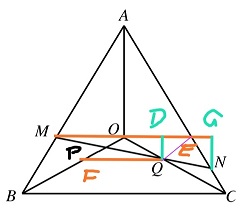
由题3已知MO//FQ且MO=FQ。再由对称性知，OFQE为平行四边形，于是EQ=OF=OQ，OQE为等腰三角形，故OE=2DE。

MDQ和MGN是一对相似三角形，于是有MD:MG=DQ:GN，即3DE:(4DE+EG)=DQ:GN。

易知ODQ和NGE也是一对相似三角形，于是有OD/DQ=GN/EG=c（c为常量，值为根号3），即DE=OD=cDQ，GN=cEG，代入上面的比例式，有

3cDQ/(4cDQ+EG)=DQ/cEG

4cDQ+EG=3c²EG

4cDQ=(3c²-1)EG

4c²DQ=(3c²-1)GN

代入c²=3，有DQ:GN=2:3。

回到最初的一对相似三角形，即有MQ:MN=2:3，于是有PQ=QN。

附言：在证明过程中留意到可以求出MP的相对长度（对直角三角形MDQ应用勾股定理），MP:DQ=根号7，MP:AB=(根号21):18，但是这对证明本身没有什么帮助。后面的过程有尝试避开根号3，但最终未能避开。

证法二（葛永超提供）：分别过点O和点P作AC的平行线交AB于点D和点E，如下图所示：

 不妨设AB=9，则BM=3。三角形ADO中，角A和角O都为30度，于是AD=DO。直角三角形BOD中角B为30度，有BD=2DO=2AD，于是AD=3，BD=6。

BPM和BOD是一对相似三角形，BE:BD=BP:BO=5:6（原题解法三里的结论），于是BE=5，ME=2。

再考虑MPE和MNA这一对相似三角形，MP:MN=ME:MA=2:6，于是MN=3MP=2MP+QN，即有QN=MP。

附言：这个证法相比上一个证法显得举重若轻，而且轻松避开了根号3。把原题的解法三里的辅助线图和这里的辅助线图放在一起，更显这两个思路的连接和美感：

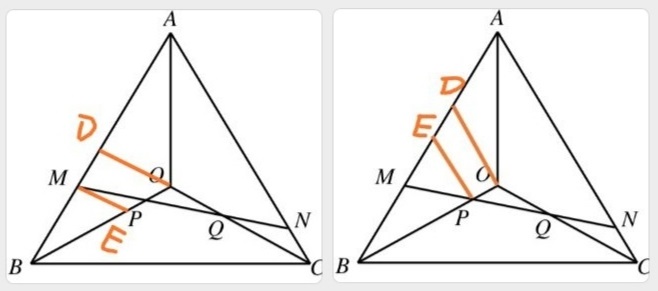
按本证法的假设AB=9，MP的长度为根号21的一半。

 

进一步，又有如下4个拓展题（共用下图）：

拓展题3：在原题的图中仅给出PQ=QN，求证：MP=PQ。

拓展题4：在原题的图中仅给出MP=QN，求证：MP=PQ。

拓展题5：在正三角形ABC的AB边上取点M使得AM=2BM，在AC边上取点N使得AN=5CN，连接MN，与OB、OC分别交于点P和点Q。求证：MP=PQ=QN。

拓展题6：在正三角形ABC的AB边上取点M使得AM=2BM，动点N在AC边上由与点M水平平齐的位置开始向点C移动，动线MN与OB、OC分别交于动点P和动点Q。在点N沿AC由起始点向下移动时，判断QN的单调特性。

 

拓展题2、3、4的通用证法一（葛永超提供）：

对上面拓展题2的证法二进行通用性扩展，记MP:PQ=1:x，仍不妨设AB=9。

先依托下图中的一对辅助线（延长CO与AB交于点D，过点M做OD的平行线交BO于点E）求出BP与BO的比值：

由△MPE~△QPO，有MP:PQ=PE:PO=1:x，即有PO=xPE

由△BME~△BDO，有BE:BO=BM:BD=2:3

于是BE=2(PE+PO)，BP=BE+PE=3PE+2PO, BO=BP+PO=3PE+3PO

综上有BP:BO=(3+2x):(3+3x)。

再依托下图中的另一对辅助线（过点O和点P分别做AC的平行线交AB于点D和点E）求出MP、PQ、QN三者的比例关系：

由△BPE~△BOD，有BE:BD=BP:BO=(3+2x):(3+3x)，再由BD=2AD=6（前述结论）知，BE=2(2x+3)/(x+1)，ME=BE-BM=BE-3=(x+3)/(x+1)。

由△MEP~△MAN，有ME:MA=MP:MN，MN=MA·MP/ME=6(x+1)MP/(x+3)，于是QN=MN-MP-PQ=MN-(x+1)MP=MP·[6(x+1)/(x+3)-(x+1)]，从而得到

MP:PQ:QN=1:x:(x+1)(3-x)/(x+3)，x的取值范围为(0,3)。

拓展题2对应1=x，此时(x+1)(3-x)/(x+3)=2·2/4=1，即有PQ=QN。

拓展题3对应x=(x+1)(3-x)/(x+3)，可化为(2x+3)(x-1)=0，由假设知x>0，故只有x=1，即有MP=PQ。

拓展题4对应1=(x+1)(3-x)/(x+3)，可化为x(x-1)=0，x=0对应的是点O、点P和点Q三点重合的情形，不合题设要求，舍去，故只有x=1，即有MP=PQ。

拓展题2、3、4的通用证法二（葛永超提供）：

连接MO并延长交AC于点D，过点Q作BC的平行线分别交OB和AC于点E和点F，如下图所示：

由前述结论知，MD//BC。设PQ/MP=x，并设AB=3。则MO=OD=1。

由△MOP~△QEP，有EQ/MO=PQ/MP=x，即EQ=x。

由△OEQ~△OBC，有OQ/OC=EQ/BC=x/3，于是QC/OC=(OC-OQ)/OC=1-x/3=(3-x)/3。

由△CQF~△COD，有QF/OD=CQ/OC，即QF=(3-x)/3。

由△QNF~△NMD，有QN:MN=(3-x)/3:2，即6QN=(3-x)(MP+xMP+QN)，可求得QN/MP=(3-x)(1+x)/(3+x)。

于是有MP:PQ:QN=1:x:(3-x)(1+x)/(3+x)，x的取值范围为(0,3)。

得到和通用证法一一样的结论。之后的三种情形考察完全一样，此处不再重复。

 

拓展题5：在正三角形ABC的AB边上取点M使得AM=2BM，在AC边上取点N使得AN=5CN，连接MN，与OB、OC分别交于点P和点Q。求证：MP=PQ=QN。

证明：连接MO并延长与AC交于点E，继续延长与过点N作MO的垂线交于点F，过点P和点Q依次作MO的垂线，垂足分别为点D和点H，如下图所示：

 不妨设AC=36，则NC=6，EC=MB=12，ME=AM=24，EF=EN/2=3，MF=ME+EF=27，FN=3*sqrt(3)。于是

△MDP~△MFN，有MD:DP=MF:FN，即MD=27·DP/[3·sqrt(3)]=3·sqrt(3)·DP。

另外由直角三角形ODP的特性知，DO=sqrt(3)·DP，于是由MD+DO=MO=12，得

3·sqrt(3)·DP+sqrt(3)·DP=4·sqrt(3)·DP=12，求得DP=sqrt(3)。

同样，由△MHQ~△MDP，可得MH=3·sqrt(3)·HQ。

再由直角三角形OHQ的特性知，OH=sqrt(3)·HQ，于是有

MH=MO+OH=12+sqrt(3)·HQ=3·sqrt(3)·HQ

即12=2·sqrt(3)·HQ，求得HQ=2·sqrt(3)。

综上有DP:HQ:FN=1:2:3=MP:MQ:MN，即有MP=PQ=QN。

 

拓展题6：点O为正三角形ABC的中心，AB边上取点M使得AM=2BM，连接MO并延长交AC于点T。动点N在AC边上由点T开始向点C移动，动线MN与OB、OC分别交于动点P和动点Q。在点N沿AC由起始点向下移动时，判断QN的单调特性。

分析：点N由点T向下朝点C移动时，MP是单调递减的，MQ和MN都是单调递增的，可以从图中直观地看出来，证明也很容易。PQ=MQ-MP，一个单调递增量减去一个单调递减量，自然是单调递增的。但QN=MN-MQ，两个单调递增的量相减，判断起来有一定难度。

利用上述拓展题2、3、4的通用证法得到的 QN/MP=(x+1)(3-x)/(x+3)=(-x²+2x+3)/(x+3)，记

u=-x²+2x+3，v=x+3，f(x)=u/v

对f(x)求导，有

v²·f'(x) = u'v-uv' = (2-2x)(x+3)+x²-2x-3 = 12-(x+3)²

由于x的取值范围为(0,3)，f'(x)=0的唯一解为x=sqrt(12)-3。从而可知，f(x)在(0,sqrt(12)-3)上单调递增的，在(sqrt(12)-3,3)上是单调递减的。

记TN为t，x=PQ/MP=(MQ-MP)/MP=MQ/MP-1，在图中可以直观看出MQ和1/MP都会随t值增大而增大，可以推断x是t的单调递增函数，因此大体推断出QN是先单调递增后单调递减，至于动点N在TC的哪个具体位置使得QN取得最大值，由上述得到的MP:PQ:QN比例关系不能推定出来，还需要想其它的办法。

【这里对QN的单调性判断有误，具体参见：对一道拓展题的重新考虑】

 

继续拓展：

拓展题7：如下图，点O为正三角形ABC的中心，点M在AB上，点N在AC上，连接MN，交OB和OC分别于点P和点Q。已知MP=PQ=QN，AN=5CN。请判断：

(1) 若QN=PQ，能否推出MP=PQ；

(2) 若MP=PQ，能否推出QN=PQ；

(3) 若QN=MP，能否推出MP=PQ。

分析与求解：

这个拓展题里，点N成了定点，而点M成了动点。初步判断这里借用不上拓展题2、3、4的通用证法二，因为NO不与BC平行。考虑借用拓展题2、3、4的通用证法一的方法。

延长BO交AC于点D，过点N作BD的平行线交OC于点E，如下图所示：

设PQ=xQN，又设AC=18，则CN=3，DN=6，AN=15。

由△OPQ~△ENQ，有PQ:QN=OQ:EQ，即OQ=xEQ。

由△NEC~△DOC，有CE:CO=CN:CD=3:9，即CO=3CE。

由EQ+OQ=EO=CO-CE=2CE，有(x+1)EQ=2CE，CE=(x+1)EQ/2。

于是CQ:CO=(CE+EQ):(CE+EQ+OQ)=(x+3)/2:(3x+3)/2=(x+3):3(x+1)。

如下图所示，分别过点O和点Q作AB的平行线交AC于点D和点E。

三角形ADO中，∠A=∠O=30°，AD=OD。DOC为直角三角形，且∠ODC=60°，于是DC=2OD=2AD，得到OD=AD=AC/3=6，CD=12。

由△CQE~△COD，有CQ:CO=CE:CD，即有CE=CD·(CQ/CO)=12·(x+3)/[3(x+1)]=4(x+3)/(x+1)，于是NE=CE-CN=CE-3=(x+9)/(x+1)。

由△EQN~△AMN，有QN:MN=NE:NA，即

(x+9)·MN = 15(x+1)·QN

(x+9)·[MP+(1+x)QN] = 15(x+1)·QN

(x+9)·MP = (15-x-9)(x+1)QN

MP/QN = (6-x)(x+1)/(x+9)

于是得到

QN:PQ:MP=1:x:(6-x)(x+1)/(x+9)，x∈(0,6)。

分情形考虑：

(1) 若QN=PQ，则x=1，(6-1)(1+1)/(1+9)=5·2/10=1，可以推出MP=PQ；

(2) 若MP=PQ，则x=(6-x)(x+1)/(x+9)，即x²+9x+x²-5x-6=2x²+4x-6=0，即(x+3)(x-1)=0，只有x=1符合，此时可以推出QN=PQ；

(3) 若QN=MP，则1=(6-x)(x+1)/(x+9)，即x+9+x²-5x-6=x²-4x+3=(x-1)(x-3)=0，得到x=1和x=3两个解，此时不可以推出QN=PQ。当x=3时，MN//BC，PQ=3MP=3QN。

 

再次拓展：

拓展题8：如下图，点O为正三角形ABC的中心，动点M在AB上，动点N在AC上，连接MN，交OB和OC分别于点P和点Q。试求可以作出多少条满足MP=PQ=QN的线段MN来。

 分析与求解：

继续沿用拓展题7的做法。设PQ=xQN，设AC=18，设CN=t，易知t∈(0,9)，因为当t>=9时，无论在AB上怎么取点M，MN都不能保证与OB和OC各有一个交点。

由△OPQ~△ENQ，有PQ:QN=OQ:EQ，即 OQ=xEQ。

由△NEC~△DOC，有CE:CO=CN:CD=t:9，即 CO=9CE/t。

由CO=OQ+EQ+CE=(1+x)EQ+CE=9CE/t，有

(1+x)EQ=(9-t)CE/t

EQ/CE=(9-t)/(t+tx)

于是CQ/CO = (CE+EQ)/(9CE/t) = t/9 + (9-t)/(9x+9)。

继续考察下图所示的情形：

由前述结论，有OD=AD=AC/3=6，CD=12。

由△CQE~△COD，有CQ:CO=CE:CD，即有CE = CD·(CQ/CO) = 12 · [t/9 + (9-t)/(9x+9)] = 4t/3 + 4(9-t)/(3x+3)，于是

NE = CE - CN = CE - t = t/3 + 4(9-t)/(3x+3) = (tx-3t+36)/(3x+3)。

由△EQN~△AMN，有QN:MN=NE:NA，即

(tx-3t+36)·MN = (18-t)(3x+3)·QN

(tx-3t+36)·[MP+(1+x)QN] = (54-3t)(x+1)·QN

(tx-3t+36)·MP = (54-3t-tx+3t-36)(x+1)QN = (18-tx)(x+1)QN

MP/QN = (18-tx)(x+1)/(tx-3t+36)

于是得到

QN:PQ:MP = 1:x:(18-tx)(x+1)/(tx-3t+36)。

要满足QN=PQ=MP，则有1=x=(18-tx)(x+1)/(tx-3t+36)

把x=1代入(18-tx)(x+1)/(tx-3t+36)=1，有

(18-t)·2/(36-2t)=1，即 18 - t = 18 - t。这说明，只要QN=PQ，就一定有PQ=MP，这个结论和t的取值没有关联关系。

由对称性，也说明，只要MP=PQ，就一定有PQ=QN。

对于QN:PQ:MP = 1:x:(18-tx)(x+1)/(tx-3t+36)，可以使用更加通用的变量 y=t/9 来替代 t 来表达，即

QN:PQ:MP = 1:x:(2-xy)(x+1)/(xy-3y+4)

这里，变量 y 的含义是NC:AC/2，即NC与正三角形边长的一半的比值，由本题开头的分析可知， y∈(0,1)。

如下图所示，N在GC上移动（M在BF上移动），点G、点E、点K分别对应y=1、y=2/3、y=1/3。

取y=1/3，QN:PQ:MP=1:x:(6-x)(x+1)/(x+9)，与拓展题7推出的比例式一致。

取y=2/3，QN:PQ:MP=1:x:(6-2x)(x+1)/(2x+6)=1:x:(3-x)(x+1)/(x+3)，与拓展题2、3、4通用证法推出的比例式一致。

由拓展题5可知，当y=2/3时，确实有QN=PQ=MP，此时MN就是HE；由对称性可知，当y=1/3时，也确实有QN=PQ=MP，此时MN就是DK。

取y∈(2/3,1)，例如图中红色线段所示，点N固定在GE中某个点的位置，随着动点M下行，直观看来，NQ是递减的，PQ是递增的，因此一定存在唯一的动点M使得QN=PQ，由上述推论，知此时也有MP=PQ。于是可以推断会有无数条MN满足MP=PQ=QN。

 

对称地，引入变量z，其含义为MB与正三角形边长的一半的比值，由上面探索出的一些结论，可以猜测有如下命题成立：

拓展题9：当且仅当y+z=1时，MP=PQ=QN。

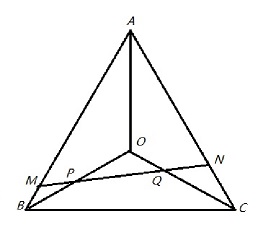
证明：

步骤一：前面的推导给出了MP、PQ、QN三个线段的比例通式，还可以进一步给出BM和NC（也是y和z）的约束关系，这一步的关键思路由葛永超提供。具体如下：

 延长BO交AC于点D，过点N作BD的平行线与OC交于点E，如下图所示：

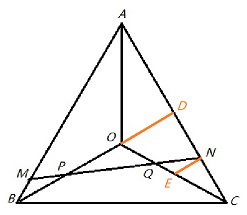
 不失一般性，假设AB=6k，BM=zAB/2=3zk，CN=yAC/2=3yk，CD=AC/2=3k；再设PQ=xQN

由△PQO~△NQE，有PQ:QN=OQ:EQ=x:1，即有OQ=xEQ，EO=OQ+EQ=(x+1)EQ

由△CNE~△CDO，有CE:CO=CN:CD=3yk:3k=y:1，即有CE=yCO，EO=CO-CE=(1-y)CO

于是EO=(x+1)EQ=(1-y)CO，EQ/CO=(1-y)/(x+1)

CQ/CO=(CE+EQ)/CO=y+EQ/CO= y+(1-y)/(x+1)=(xy+1)/(x+1)

过点O和点P分别作AB的平行线交AC于点F和点G，如下图所示：

由前述结论知，AF=OF=AC/3=2k，CF=4k

由△CQG~△COF，有CQ/CO=CG/CF=(xy+1)/(x+1)，即有CG=4k(xy+1)/(x+1) ，GQ=CG/2=2k(xy+1)/(x+1)

NG=CG-CN=4k(xy+1)/(x+1)-3yk=k(xy-3y+4)/(x+1)

由△NQGE~△NMA，有QN:MN=NG:AN=GQ:AM，即有

MN·NG=AN·QN　　　　①

AN·GQ=NG·AM　　　　②

由①有

[MP+(x+1)QN]·k(xy-3y+4)/(x+1) = (6k-3yk)·QN

[MP+(x+1)QN]·(xy-3y+4)/(x+1) = (6-3y)·QN

MP·(xy-3y+4)/(x+1) = QN·(6-3y-xy+3y-4)

MP/QN=(2-xy)(x+1)/(xy-3y+4) 

于是有

QN:PQ:MP=1:x:(2-xy)(x+1)/(xy-3y+4)　　③

这是前面已经推导过的结论。

由②有

(6k-3yk)·2k(xy+1)/(x+1) = k(xy-3y+4)/(x+1)·AM

(6-3y)·2k(xy+1) = (xy-3y+4)·AM

AM=6k(2-y)(xy+1)/(xy-3y+4)

另外，AM=AB-MB=6k-3zk

于是有

6k-3zk = 6k(2-y)(xy+1)/(xy-3y+4)

(2-z)(xy-3y+4) = 2(2-y)(xy+1)　　　　④

这便是y和z的约束关系。

步骤二：证明命题的必要性：由MP=PQ=QN推出y+z=1

已知MP=PQ=QN，由③可知，x=1，代入④，得到

(2-z)(4-2y)=2(2-y)(y+1)

2-z=y+1

即有 y+z=1。

步骤三：证明命题的充分性：由y+z=1推出MP=PQ=QN

已知y+z=1，则有z=1-y，代入④，得到

(1+y)(xy-3y+4)=(4-2y)(xy+1)

xy-3y+4+xy²-3y²+4y=4xy+4-2xy²-2y

xy+y+4+xy²-3y²=4xy+4-2xy²-2y

3xy²-3xy+3y-3y²=0

xy-x+1-y=0

x(y-1)+1-y=(x-1)(y-1)=0

由前述结论知，y∈(0,1)，于是有x=1

即PQ=QN，再由前述的结论知，MP=PQ。

证毕。