CTC

资料

资料查询：

CTC Loss 数学原理讲解：Connectionist Temporal Classification

教程：Connectionist Temporal Classification详解补充

CTC Algorithm Explained Part 1：Training the Network（CTC 算法详解之训练篇

源代码：

https://github.com/pytorch/pytorch/blob/main/aten/src/ATen/native/LossCTC.cpp

论文：
Connectionist temporal classification: labelling unsegmented sequence data with recurrent neural networks

Connectionist Temporal Classification A Tutorial with Gritty Detail

简述

CTCLoss是一种无需数据对齐的损失函数，常用于图像文本识别和语音识别，解决了RNN处理序列数据时长度不一致的问题，通过Forward-Backward算法计算概率，并在训练中使用

CTC即论文中的 Connectionist Temporal Classification，连续形式的时序数据分类，指使用递归神经网络来标记非分段序列数据

背景

标准神经网络的目标函数是为训练序列中的每个点分别定义的，也就是对单个点计算损失，网络的目标函数是所有数据点损失的平均或求和。在训练时，模型可以针对单个数据点计算损失并更新参数，不需要同时考虑其他数据点的误差，因此可以视作各个数据点是相互独立的

基于这一点，以及不考虑跨时间步或者自监督（如BERT）的特性，RNN似乎只能训练一系列独立的标签分类，这意味着训练的序列数据必须被预分段并标记

但标记未分割序列数据是现实世界序列学习中普遍存在的困难问题，尤其是感知任务，如图像文本识别OCR，语音识别ASR，在这些领域中，所面临的一个问题是神经网络的输出与ground truth^[1]的长度不一致，导致loss难以计算

例如在OCR中，存在两个问题：

• 长度不一致：输入时间步数（如图像划分的块数）和输出标签数（如字符数）通常不同

​ 如一张图片被划分为100个时间步，但输出文本可能只有5个字符

• 位置模糊性：无法确定输出标签具体对应输入序列的哪一部分

​ 同样是图片中，一个字符可能跨越多个划分的图像中，一个划分后的小部分也可能包含多个字符的混合

由于连续序列数据的对齐难题，学者提出了一种不需要对齐的Loss计算方法：CTC Loss

总体思想

CTC Loss的计算对象是神经网络经过softmax归一化后的输出矩阵和ground truth，并且CTC Loss不要求输出矩阵和ground truth的大小相同，输出矩阵的维度为\(N \times T\)，其中 \(N\) 是类别数，\(T\) 为语音长度

CTC Loss是训练阶段的监督信号，用于调整序列分类模型的参数，具体流程：

• 模型输出：输入序列 \(x\) 经过神经网络（如RNN、Transformer）后，输出每个时间步的标签的概率分布 \(y_k^t\)（输出矩阵）
• 计算CTC Loss：基于 \(y_k^t\) 和真实标签序列l，通过Forward-Backward算法计算 \(p(l | x)\)，并得到负对数似然损失
• 反向传播：利用梯度更新模型参数，使得 \(p(l \mid x)\) 最大化

模型在每个时间步输出标签的概率分布 \(y_k^t\) ，这些概率的连乘构成路径概率 \(p(\pi | x)\) ，CTC通过边缘化对齐路径并计算损失后，调整这些概率分布，使得所有有效路径的联合概率最大化

定义 \(S\) 是从固定分布 \(D_{\Chi \times Z}\) 中采样的训练集，其中

• 输入空间（预测值）\(\Chi = (\mathbb{R}^m)^*\) 是所有 \(m\) 维实值向量序列的集合；
• 目标空间（ground truth）\(Z = L^*\) 是有限字母表 \(L\) 中所有符号序列的集合。

定义字符集 \(L' = L \cup \{\text{blank}\}\)。

\(S\) 中的每一个训练样本由一对序列 \((x, z)\) 组成，其中

• 输入序列 \(x = (x_1, x_2, \dots, x_T)\)，
• 目标序列 \(z = (z_1, z_2, \dots, z_U)\)。

序列数据预测任务中的一个基本原则是：真实值的长度不能超过预测值的长度^[2]，即

\[U \le T. \]

我们的目标是使用训练集 \(S\) 训练一个时序分类器（temporal classifier） ，使得模型能生成正确的标签序列 \(\mathcal{l}\)

\[h: \Chi \to Z. \]

定义 \(y_k^t\) 表示在时刻 \(t\) 时真实字符为 \(k\) 的概率。通俗来讲，\(y_k^t\) 是经过 softmax 之后的输出矩阵中的一个元素。

将字符集 \(L'\) 可以构成的所有序列的集合称为 \((L')^T\)，显然 \((L')^T\) 包含 \(|L'|^T\) 个序列。

将 \((L')^T\) 中的任意一个序列称为路径，并标记为 \(\pi\)。

\(\pi\) 的分布（即给定输入序列 \(x\) 后，路径 \(\pi\) 出现的概率）为：

\[p(\pi \mid x) = \prod_{t=1}^{T} y_{\pi_t}^{t} \tag{1}\ \ \ , \ \ \forall \pi \in (L')^T \]

公式（1）是将路径 \(\pi\) 中每一个字符出现的概率进行连乘，其前提条件是假设每个时刻的字符都是相互独立的，即 RNN 在不同时刻的输出是相互独立的。

定义多对一（many-to-one）映射

\[B: (L')^T \to L^{\le T} \]

例如：

\[B(\text{a - ab -}) = B(\text{-aa - aab}) = B(\text{-aa - -abb -}) = \text{aab} \]

可通过映射 \(B\) 计算得到标签 \(l \in L^{\le T}\) 的条件概率，为对应于 \(l\) 的所有可能路径的概率之和：

\[p(l \mid x) = \sum_{\pi \in B^{-1}(l)} p(\pi \mid x) \tag{2} \]

以 \(l = \text{aab}\) 为例，所有可以通过映射 \(B\) 得到 "aab" 的路径称为 \(B^{-1}(l)\)，例如路径 "a - ab -" 和 "-aa - aab" 均属于 \(B^{-1}(l)\)。

这一步解决了长度不一致的问题。

我们希望 \(p(l \mid x)\) 越大越好，因此分类器 \(h\) 的输出是使 \(p(l \mid x)\) 最大的 \(l\)，即

\[h(x) = \operatorname*{argmax}_{l \in L^{\le T}}\ p(l \mid x) \tag{3} \]

CTC的Loss函数也是基于这个目标设计的

\[\mathcal{L}_{\text{CTC}} = -\log\ p(\ell \mid \mathbf{x}) = -\log \sum_{\pi \in \mathcal{B}^{-1}(\ell)} p(\pi \mid \mathbf{x}) \]

传统的需要数据对齐的损失函数是基于每一帧数据（单个数据点）来最小化误差，而 CTC 的目标是基于整个训练序列来最大化 \(p(l \mid x)\) 。

把寻找 \(\operatorname*{argmax}_{l \in L^{\le T}}\ p(l \mid x)\) 的路径的任务称为解码。最简单的解码方式自然是暴力穷举计算，但其计算复杂度极高。

以 25 ms 的语音作为一帧，则长度为 1 秒的语音包含 40 帧。考虑一段 5 秒长（200 帧）的英文语音，其输出矩阵包含 \(27^{200} \approx 1.87 \times 10^{286}\) 条路径，几乎无法计算。

为了简化计算，借鉴 HMM（Hidden Markov Model，隐马尔可夫模型）中的 Forward–Backward 算法思路，利用动态规划算法求解。因此 CTC Loss 本质上是一种动态规划算法（Dynamic Programming, DP）。

如果只是单向的DP也可以得到整条路径的概率，但是通过前向和后向概率的乘积，就可以得到当前某个标签在所有有效路径中的贡献，更新时可以对单个位置调整概率分布

Forward-Backward 算法

合法路径的约束条件

根据我们的映射规则以及为了使得所有路径在图中都有唯一的、合法的表示，我们需要设定一些约束（基于我们已经将blank插入了相邻的字符之间）：

1. 转换只能往右下方向，其他方向不允许
2. 相同的字符之间起码要有一个空字符
3. 非空字符不能被跳过
4. 起点必须从前两个字符开始（因为第一个字符是blank可以跳过）
5. 终点必须落在结尾两个字符

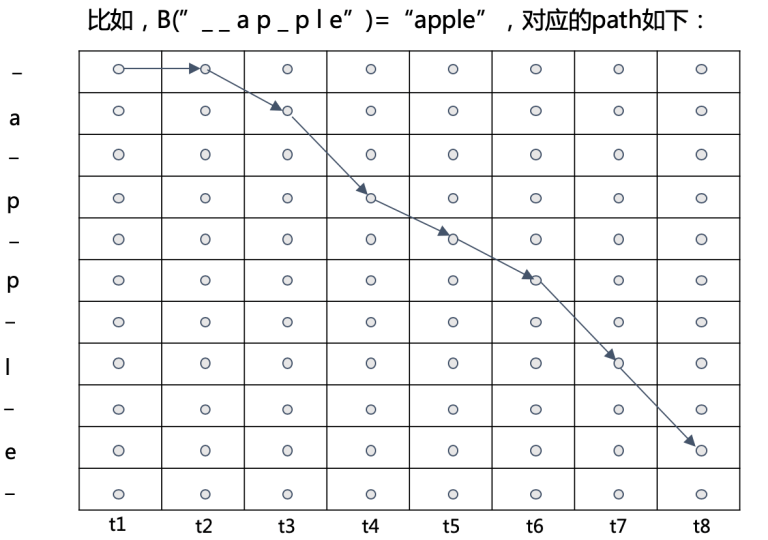
这些约束规则导致合法路径的数量大大减少，根据以上约束规则，所有映射为 \(l\) = apple 的合法路径为

Forward-Backward算法的数学推导

给定一个长度为 \(r\) 的序列 \(q\)，记

• \(q_{1:p}\) 为序列 \(q\) 的前 \(p\) 个元素；
• \(q_{r-p:r}\) 为序列 \(q\) 的后 \(p\) 个元素。

对于 ground-truth 标签 \(l\)，定义前向变量

\[\alpha_t(s) = \sum_{\substack{\pi\in(N)^T\\B(\pi_{1:t})=l_{1:s}}}\; \prod_{t'=1}^{t} y_{\pi_{t'}}^{t'} \tag{5} \]

来表示序列 \(l_{1:s}\) 在时刻 t 的全概率

其中

• \(\prod_{t'=1}^{t} y_{\pi_{t'}}^{t'}\) 表示子序列 \(\pi_{1:t}\) 的联合概率（全概率）；

• \(B(\pi_{1:t})=l_{1:s}\) 表示：在所有长度为 \(t\) 的子序列 \(\pi_{1:t}\) 中，只有那些经映射 \(B\) 后等于目标前缀 \(l_{1:s}\) 的才被计入求和。

• 约束：\(t \ge s\)。

  示例：\(\pi_{1:6} = \{\texttt{-c a a - t}\}\) ，长度为 \(t=6\)，目标前缀 \(l_{1:3}=\texttt{cat}\) 长度为 \(s=3\)。

类似地，定义后向变量

\[\beta_t(s) = \sum_{\substack{\pi\in(N)^T\\B(\pi_{t:T})=l_{s:|l|}}}\; \prod_{t'=t}^{T} y_{\pi_{t'}}^{t'} \tag{6} \]

其中

• 求和范围是所有满足 \(B(\pi_{t:T})=l_{s:|l|}\) 的子序列 \(\pi_{t:T}\)；
• \(\prod_{t'=t}^{T} y_{\pi_{t'}}^{t'}\) 表示从时刻 \(t\) 到 \(T\) 的联合概率。

前向和反向过程计算示意图如下，这些概率都可以递归求解，或者说，某个前缀的概率是更长前缀概率的子问题，因此可以用动态规划求解

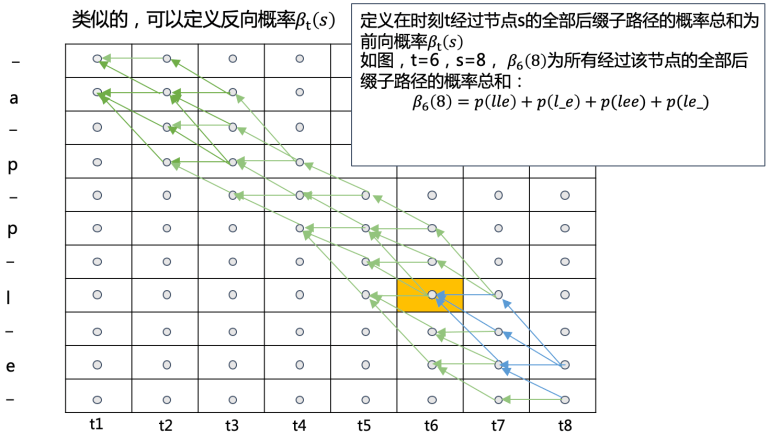
然后通过前向概率和后向概率就可以计算 CTC Loss。

以前向过程为例， \(\alpha_t(s)\) 可以通过 \(\alpha_{t-1}(s)\) 和 \(\alpha_{t-1}(s-1)\) 计算得到，并不需要直接计算 \(p(l|x)\)，而是通过递归的方式来得到 \(p(l|x)\)。后向过程同理，\(\beta_t(s)\) 可以通过 \(\beta_{t+1}(s)\) 和 \(\beta_{t+1}(s+1)\) 计算得到。

用 \(y_t^k\) 表示在时刻 \(t\) 时真实字符为 \(k\) 的概率。用 \(b\) 表示 blank，则可定义初始状态：

\[\begin{aligned} \alpha_1(1) &= y_b^t \\ \alpha_1(2) &= y_{l_1}^t \\ \alpha_1(s) &= 0,\quad \forall s > 2 \end{aligned}\tag{7} \]

CTC Loss 的前向过程为：

\[\alpha_t(s) = \begin{cases} \bigl[\alpha_{t-1}(s) + \alpha_{t-1}(s-1)\bigr]\,y_{l'_s}^t, & \text{if } l'_s = b \text{ or } l'_{s-2} = l'_s \\[6pt] \bigl[\alpha_{t-1}(s) + \alpha_{t-1}(s-1 ) +\alpha_{t-1}(s - 2)\bigr]\,y_{l'_s}^t, & \text{otherwise} \end{cases} \tag{8} \]

如果是\(l'_{s-2} = l'_s\)，意味着目标序列中相邻两个字符是相同，那么根据我们的约束条件，当前状态不能从\(\alpha_{t-1}(s-2)\)处转移得到，而如果\(l'_s = b\)，那说明\(s - 1\)是一个有效字符，如果直接从\(s-2\)转移那么会跳过该字符，这同样是不允许的，因此这两种情况特殊判断；其他情况即可以在当前位置继续向右移动，或者从blank处转移，或者直接从上一个有效字符处转移

后向过程的递推公式与（8）类似，此处省略。

这种方法可以比较直观简单地得到\(p(l|x)\)，但一定程度上可能会造成数值下溢的问题

CTC的训练

通过上面的计算过程可以知道，CTC是使用一种概率的形式来表示目标路径的，作为一种概率方法，采用常用的最大似然方法训练 CTC。模型训练的目的是同时最大化训练集中所有正确分类的概率，最大化 $ p(\ell \mid \mathbf{x}) $ 即最小化目标函数（CTC Loss函数）：

\[\mathcal{O}_{\mathrm{ML}}(S, \mathcal{N}_{w}) = -\sum_{(\mathbf{x},\ell)\in S} \log p(\ell \mid \mathbf{x}) \tag{11} \]

采用梯度下降法训练网络，则需要对式（11）求导。由于训练集中的样本是独立的，可以对每组样本 \((\mathbf{x},\ell)\in S\) 单独求导，即

\[\frac{\partial\mathcal{O}_{\mathrm{ML}}\bigl((\mathbf{x},\ell),\mathcal{N}_{w}\bigr)}{\partial y_{k}^{t}} = -\frac{\partial\log p(\ell \mid \mathbf{x})}{\partial y_{k}^{t}} \tag{12} \]

损失函数必须是数学形式可导的，于是接下来考虑使用 Forward-Backward 算法计算公式（12）。已知：

\[\begin{aligned} \alpha_t(s) &= \sum_{\substack{\pi \in N^T\\ \mathcal{B}(\pi_{1:t})=\ell_{1:s}}} \prod_{t'=1}^{t} y_{\pi_{t'}}^{t'} \\[6pt] \beta_t(s) &= \sum_{\substack{\pi \in N^T\\ \mathcal{B}(\pi_{t:T})=\ell_{s:|\ell|}}} \prod_{t'=t}^{T} y_{\pi_{t'}}^{t'} \end{aligned} \]

则对于任意时刻 t ，都有：

\[\alpha_t(s)\,\beta_t(s) = \sum_{\substack{\pi\\ \mathcal{B}(\pi)=\ell\\ \pi_t=\ell'_s}} y_{l'_s}^t \ \prod_{t=1}^{T} y_{\pi_{t}}^{t} \tag{13} \]

以\(T = 6,\ l=ab\) 且 \(t\) 取4， \(s\) 取3，说明式13

\[\begin{aligned} \alpha_t(s) = \alpha_4(3) &= p(\texttt{--a-}) + p(\texttt{-a--}) + p(\texttt{aaa-}) + p(\texttt{a---}) \\[4pt] \beta_t(s) = \beta_4(3) &= p(\texttt{--b}) + p(\texttt{-bb}) + p(\texttt{-b-}) \end{aligned} \]

• 前向过程共有 4 条路径，均满足

  \(\pi \in \mathcal{N}^T,\ \mathcal{B}(\pi_{1:t=4}) = \ell_{1:s=3} = \texttt{"-a-"} = \texttt{"a"}\)

• 后向过程共有 3 条路径，均满足

  \(\pi \in \mathcal{N}^T,\ \mathcal{B}(\pi_{t=4:T=6}) = \ell_{s=3:|\ell|=5} = \texttt{"-b-"} = \texttt{"b"}\)

以 \(y_{\ell'_s}^t\) 表示图中 \((t=4,s=3)\) 节点的概率，则共有 \(3 \times 4 = 12\) 条经过节点 \(\ell_s\) 的路径可以通过映射获得 \(\ell = \texttt{ab}\)。3 为前半部分的路径条数，4 为后半部分的路径条数，两两组合即为所有可能的情况，这些路径表示为

\[\pi \in \mathcal{B}^{-1}(\ell=\texttt{ab})\quad and\quad\pi_{t=4}=\ell'_s \]

其中任意一条路径的全概率可以表示为

\[\prod_{t=1}^{T} y^t_{\pi_t},\quad \pi \in \mathcal{B}^{-1}(\ell),\ \pi_t = \ell'_s \]

\(\alpha_4(3)\) 和 \(\beta_4(3)\) 的全概率计算公式中均包含 \(y_{l'_s}^t\)，则 \(\alpha_4(3)\,\beta_4(3)\) 中包含 \({y_{l'_s}^t}^2\)，因此可得 公式 (13)：

\[\alpha_t(s)\,\beta_t(s) = \sum_{\substack{\pi\\ \mathcal{B}(\pi)=\ell\\ \pi_t=\ell'_s}} y_{l'_s}^t \ \prod_{t=1}^{T} y_{\pi_{t}}^{t} \]

简单来说，\(\alpha_t(s)\)表示了路径的前半部分，\(\beta_t(s)\)代表了路径的后半部分，我们从这两者中任意拿出一项都是可以组合成一条完整的路径的，不过因为这两项都包含了 \((t, l_s')\) 这一节点，因此乘积为

\[y_{l_s'}^t \prod_{t=1}^T y_{\pi_t}^t\ \\ \mathcal{B}(\pi)=l\quad and \quad \pi_t = l_s' \]

这是乘积中的一项，代表了其中一条合法路径，而 \(\alpha_t(s)\) 和 \(\beta_t(s)\) 的乘积是所有的路径，所以式（13）的累加符号中为 \(\mathcal{B}(\pi)=l\)

将式 (13) 变形后和式 (1) 的形式，即 \(p(\ell \mid \mathbf{x}) = \sum_{\pi \in \mathcal{B}^{-1}(\ell)} \prod_{t=1}^T y_t^{\pi_t}\)，对比

\[\begin{align} &\alpha_t(s)\beta_t(s) = y^t_{\ell'_s} \sum_{\substack{\pi \in \mathcal{B}^{-1}(\ell)\\ \pi_t = \ell'_s}} p(\pi \mid \mathbf{x})\\ \to\ &\frac{\alpha_t(s)\beta_t(s)}{y^t_{\ell'_s}} = \sum_{\substack{\pi \in \mathcal{B}^{-1}(\ell)\\ \pi_t = \ell'_s}} p(\pi \mid \mathbf{x}) \tag{14} \end{align} \]

知 \(\frac{\alpha_t(s)\beta_t(s)}{y^t_{\ell'_s}}\) 是所有经过\(l'_s\)的路径的集合（的概率），于是对所有满足 \(\pi_t = \ell'_s\) 的路径集合，在任意时刻 \(t\)，可以得到

\[\sum_{s=1}^{|l'|}\frac{ \alpha_t(s)\beta_t(s)}{y^t_{\ell'_s}} = p(\ell \mid \mathbf{x}) \tag{15} \]

\(\frac{\alpha_t(s)\beta_t(s)}{y^t_{\ell'_s}}\) 保证了是所有经过 \(l'_s\) 的有效路径的集合，同时任何有效路径 \(\pi \in \mathcal{B}^{-1}(l)\) 在时间 t 必须经过某个 \(l_s'\)，即所有有效路径按 \(\pi_t\) 的值被分到不同 s 的\(\frac{\alpha_t(s)\beta_t(s)}{y^t_{\ell'_s}}\)中，求和 \(\sum_s\) 又覆盖了所有可能的\(\pi_t\)，等价于覆盖了所有的有效路径，并且与时间 t 无关，所以得到的结果就是有效路径的概率和，为 \(p(\ell \mid \mathbf{x})\)

式（15）使我们可以对上面的求导形式继续计算，令 \(lab(l,k)=\{s\mid l'_s=k\}\) ，也就是扩展序列 \(l'\) 中所有等于标签 k 的位置 s 的集合，例如目标序列\(l = [A, B]\)，扩展序列 \(l' = [-, A, -, B, -]\)，若 \(k = -\)，则 \(lab(l, -) = {1, 3, 5}\)

之所以需要定义这个集合，是因为我们要计算偏导，而 \(y_k^t\) 仅影响那些 \(l_s' = k\) 的项，即 \(s \in lab(l, k)\)，其余项的导数就为0

于是 \(\sum_{s\in lab(l,k)}\frac{\alpha_t(s)\beta_t(s)}{y_k^t}\) 表示在 \(t\) 时刻经过 \(l'_s = k\) 的所有路径的集合

式 (15) 对 \(y_k^t\) 求导，因为 \(\alpha_t(s)\beta_t(s)\) 中并不包含 \(y_k^t\) 相关的项，因此只需要对 \(\frac{1}{y_k^t}\) 求导，得到结果如下：

\[\frac{\partial \ p(l|x)}{\partial y_k^t}=\frac{1}{{y_k^t}^2}\sum_{s\in lab(l,k)}\alpha_t(s)\beta_t(s) \]

则目标函数关于网络经过 softmax 归一化后的输出数据的偏导数为：

\[\frac{\partial\ln\!\bigl(p(l|x)\bigr)}{\partial y_k^t} = \frac{1}{p(l|x)}\frac{\partial p(l|x)}{\partial y_k^t}=\frac{1}{p(l|x){y_k^t}^2}\sum_{s\in lab(l,k)}\alpha_t(s)\beta_t(s) \tag{16} \]

为了通过 softmax 层进行梯度反传，我们需要得到目标函数关于未经过 softmax 归一化的参数 \(u_k^t\) 的导数

\(u_k^t\)是 softmax 层的输入（logits），即在时间步 t 对标签 k 的未归一化得分，\(y_k^t\) （标签概率）定义为 \(y_k^t = \frac{e^{u_k^t}}{\sum_{k'}e^{u^t_{k'}}}\)

\(\mathcal{L}\)是指负对数似然，也就是\(-log\ p(l | x)\)，\((x, z)\) 表示输入数据 \(x\) 和真实标签序列 \(z\)（即 \(l\) ），\(N_w\) 指的是神经网络模型，参数为 \(w\)，这种写法强调损失函数依赖于输入数据、真实标签和参数模型

\(\mathcal{L}\) 对 \(y_{k'}^t\) 的梯度由式（16）得到（注意 \(\mathcal{L}\) 是负对数似然）

\[\frac{\partial\mathcal{L}}{\partial y_{k'}^t}=-\frac{\partial\ln\!\bigl(p(l|x)\bigr)}{\partial y_{k'}^t} = -\frac{1}{p(l|x)}\frac{\partial p(l|x)}{\partial y_{k'}^t}=-\frac{1}{p(l|x){y_{k'}^t}^2}\sum_{s\in lab(l,k')}\alpha_t(s)\beta_t(s)\\ \]

\(y_k^t\) 对 \(u_k^t\) 的梯度，即为softmax的导数，简单起见，用一般softmax形式表示，即\(y_j = \frac{e^{u_j}}{\sum_i e^{u_i}}\)，计算\(\frac{\partial y_j}{\partial u_k}\)

• \(j = k\) 时有：

\[\frac{\partial y_k}{\partial u_k} = \frac{e^{u_k}\sum_ie^{u_i}-e^{u_k}e^{u_k}}{(\sum_i e^{u_i})^2} = y_k(1-y_k) \]

• \(j \neq k\) 时，\(\frac{\partial e^{u_j}}{\partial u_k} = 0\)，也就是分子的第一项为0，此时\(\frac{\partial y_k}{\partial u_k} = - y_jy_k\)
• 于是softmax 的 Jacobian矩阵 的元素用示性函数表示就是 \(y_j(𝕀(j = k)-y_k)\)）

注意这里链式法则不能简单地表示成\(\frac{\partial \mathcal{L}}{\partial u_k^t} = \frac{\partial \mathcal{L}}{\partial y_k^t}\cdot\frac{\partial y_k^t}{\partial u_k^t}\)，如果这样写那隐含了一个假设，也就是 \(y_k^t\) 只依赖于 \(u_k^t\)，即输出之间是独立的，但在结构化预测（如RNN）中，输出 \(y_k^t\) 通常是依赖于整个输入序列 \(u^t = {u_1^t, u_2^t, \cdots}\) 的，这从softmax的分母是个累加中也能看出，所以在结构化模型中必须考虑所有可能的路径，因此需要对所有可能的 \(y_{k'}^t\) 求和：\(\frac{\partial\mathcal{L}}{\partial u_k^t}=\sum_{k'}\frac{\partial\mathcal{L}}{\partial y_{k'}^t}\cdot\frac{\partial y_{k'}^t}{\partial u_k^t}\)，这个求和反映了 \(u_k^t\) 的变化可能通过多个 \(y_{k'}^t\) 影响最终的损失

再带入上面得到的式子后即可得到导数，计算过程中注意，因为我们的 \(k'\) 实际就是遍历了所有可能的情况，因此 \(\sum_{k'} \frac{1}{y_{k'}^t}\sum_{s \in lab(l, k')}\alpha_t(s)\beta_t(s)\)

\[\frac{\partial\mathcal{L}\!\bigl((x,z),N_w\bigr)}{\partial u_k^t} = y_k^t - \frac{1}{y_k^tp(l|x)}\sum_{s\in lab(l,k')}\alpha_t(s)\beta_t(s) \tag{17}\\ where\quad p(l|x)=\sum_{s=1}^{|l'|}\frac{\alpha_t(s)\beta_t(s)}{y^t_{l_s'}} \]

从直接的形式上看，前一项 \(y_k^t\) 是模型当前预测的概率，可理解为模型认为是标签 k 的置信度，后一项的分子表示所有经过 k 的有效路径的概率和，分母可看作是归一化因子，来确保梯度比例合理

这个损失函数类似于分类任务中的标准Softmax，不过这里使用了路径概率的加权和替代了硬标签 \(𝕀(k = k')\)

如果 k 是正确标签，那么后一项的数值趋近于 1，因为有大多数有效路径经过 k ，因此这个求和值接近于 \(p(l \mid x)\)，于是 \(\frac{\partial{\mathcal {L}}} {\partial{u_k^t}} \approx y_k^t - 1\)，而 \(y_k^t \in (0, 1)\)，所以梯度为负，则根据更新公式，\(u_k^t\) 增加，\(y_k^t\)增加，即正确标签概率增大；相反， k 是错误标签时，目标项趋于 0，梯度为正，于是标签概率减小

公式 (17) 中所有参数均可以通过线性计算得到，因此 CTCLoss 可以对网络中任意一个参数求偏导以实现参数更新。

Forward-Backward的结果正是分子中的概率和，从而能明确每个时间步的标签如何影响整体序列概率，进而基于此来调整概率分布

以单层LSTM作为RNN网络，RNN-CTC模型的总体结构为：

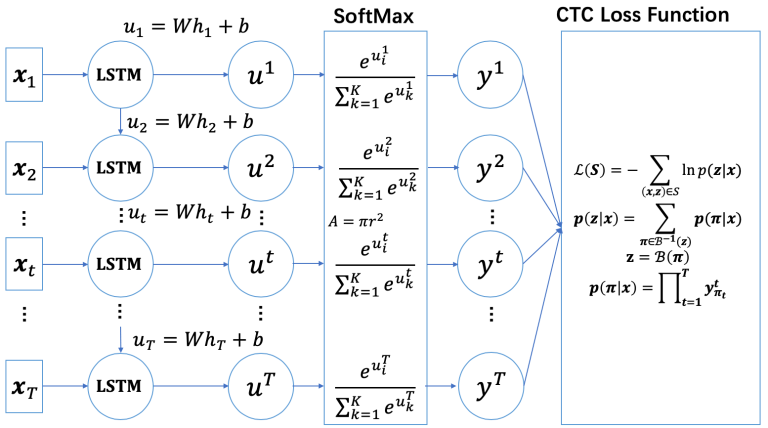
解码算法

与一般的离散型数据和对齐的序列数据的预测任务不同，在没有对齐的序列数据学习问题中，模型的预测过程本质是一个空间搜索过程，称为解码过程（也就是在模型的推理（测试）阶段使用）。

因为在对输入输出对齐的任务中，模型可以一对一预测每个位置的输出，而在没有对齐的信息中，模型不能直接一步得出整个输出，而是需要一步一步地生成一个序列，而每一步都取决于之前生成的内容，换言之，是从大量可能的输出中搜索出一个合理的输出序列，因此称为一个搜索空间的问题

如何在限定的时间条件下搜索到最优解是一个非常有挑战性的问题。尽管我们并不知道通用的、易处理的解码算法，但如下解码算法在实践中证明具有良好的解码结果：

(1) 最佳路径解码（Best Path Decoding）

\[h(x) \approx B(\pi^*)\\ where\quad \pi^* = \arg\max_{\pi \in \mathcal{N}_t}\ p(\pi \mid x) \]

\(\pi^*\) 选择每个时刻上概率最大的符号作为最佳路径。这也是预测离散型数据和对齐的序列数据的解码方式。

最佳路径解码计算起来很简单，但并不能保证：\(B(\pi^*) = \arg\max_{l \in L^{\le T}}\ p(l \mid x)\)

这个问题主要来自于我们最大化的目标是标签序列 \(l\) 的总概率，是多个路径的概率之和，但是最佳路径解码中， \(\pi*\) 只选择了其中概率最大一个路径，再得到对应的标签序列，而单一的路径概率显然无法和标签序列概率等价

较为合适的就是使用 Beam Search Decoding （束搜索解码）或者 Prefix Search （前缀搜索解码）

(2) 束搜索解码（Beam Search Decoding）

束搜索是一种近似搜索策略，用来在指数级搜索空间中高效找出前若干个最可能的序列

在CTC 解码中，束搜索的流程大致如下：

1. 从左到右处理每个时间步 t
2. 在每个时间步保留 top B 个概率最大的前缀路径 （即 beam width = B）
3. 对每个前缀，尝试扩展所有可能的下一个字符
4. 合并那些 collapse 后相同标签序列的路径
5. 最终从所有路径中选择概率最大的 collapse 结果

在这个算法中合并了多个高概率路径，能避免最佳路径法中的“路径贪心”问题

(3) 前缀搜索解码（Prefix Search Decoding）

前缀搜索解码能确保找到最优解，但最坏情况下耗时可能会随着序列长度呈指数增长。

它是束搜索的一个特殊形式，但比普通束搜索更贴合 CTC 的动态规划结构

核心思想是：

• 枚举每一个标签序列前缀 \(l\) ，维护两种概率：
  • 以 blank 结尾的路径的概率 \(p_{blank}(l, t)\)
  • 以非 blank 结尾的路径的概率 \(p_{nonblank}(l, t)\)
  • 相当于动态规划中的两个状态 \(dp[0/1]\)
• 然后递归更新当前前缀的概率（来自上一时间步）
• 最终累加所有前缀结尾为 \(l\) 的路径概率，得到 \(p(l \mid x)\)

CTC Loss 的优缺点

CTC最大的优点是不需要数据对齐，此外，因为CTC Loss依据概率计算，于是可以无缝地用于任何逐步输出概率分布的神经网络模型

CTC的缺点来源于三个假设或约束：

1. 输出独立性假设：CTC 假设每个时间片的输出是条件独立的，但在OCR或者语音识别中，相邻几个时间片中往往包含着高度相关的语义信息，它们并非相互独立的，所以某些情境下 CTC 需要语言模型（LM）辅助才能达到较好效果

2. 单调对齐：CTC 要求输入与输出之间的对齐是单向的，在OCR和语音识别中，这种约束是成立的。但是在一些场景中（如机器翻译），这个约束并不成立，也就是不合适标签间存在强依赖的任务

3. 标签学习：CTC 在没有约束时可能会将输出对齐得非常分散、不合理，模型可能会用blank大量填充，同时 CTC 也不能很好地建模重复特征，因为这依赖于 blank 分割，如果 blank 学不好，就容易导致输出错误，同时也因为模型可能对重复符号不敏感

---

1. Ground Truth 指在机器学习或数据科学中，人工标注或客观事实提供的准确、权威的参考答案。它是模型训练和评估的标准，用于监督学习中的标签或验证模型预测的正确性 ↩︎

2. 训练时，模型需要将预测序列与真实序列逐元素对比计算损失，如果真实序列更长，模型会因“预测不足”无法覆盖所有真实值，如多出的部分无对应值，进而导致损失函数无法计算 ↩︎