学习笔记: 因子分解机(Factorization Machines, FM)
2021/8/6
FFM
相比FM的改进: 当特征$x_i$与每个$x_j$交叉时, 会根据$x_j$所属的不同field, 贡献出不同的隐向量$v_{if_j}$用于内积求权重.
具体地, FFM的特征组合项为:
$$ y(x) = \omega_0 + \sum_{i=1}^n \omega_i x_i + \sum_{i=1}^{n-1} \sum_{j=i+1}^n <v_{if_j}, v_{jf_i}>x_i x_j $$
- 当特征$i$与不同field的特征$j$进行交叉时, 会提供不同的隐向量贡献 $v_{i, f_j}$. 这里$f_j$指特征$j$所处的field, 可能有若干个特征属于同一field.于是我们注意到, 相比FM的$nk$个参数, FFM的参数更多, 为$nFk$个. 其中$n$为特征数, $k$为每个隐向量的size, $F$为fields的数量.
- 注意: 当field只有一个时, FFM退化为FM.
- 此外,由于隐向量与field相关,FFM二次项并不能够化简,其预测复杂度是 $O(n^2 k)$.
FM
source: 推荐算法(一)——FM因式分解(原理+代码) - 知乎 (zhihu.com)
FM 作为推荐算法广泛应用于推荐系统及计算广告领域,通常用于预测点击率 CTR(click-through rate)和转化率 CVR(conversion rate)。
背景: Logistics回归作为线性模型, 有复杂度低, 方便求解的优点, 但缺点是没有考虑特征间的交叉, 表达能力有限.
相比线性模型的改进:
1.FM在线性模型的基础上增加了特征之间的二阶交叉. 下面我们假设特征数为$n$, 特征为$x_1, x_2,\ldots, x_n$. 交叉项可以有两种表达形式.
1.1 交叉项形式一: 如果采用$\omega_{ij}x_i x_j$的交叉项形式, 参数$\omega_{ij}$对应的偏导数为$x_i x_j$, 仅在都非0的时候参数才会得到更新.但如果有onehot特征, 数据非常稀疏, 将导致大部分参数难以得到充分训练.
$$ y(x) = \omega_0 + \sum_{i=1}^n \omega_i x_i + \sum_{i=1}^{n-1} \sum_{j=i+1}^n \omega_{ij} x_i x_j $$
1.2 交叉项形式二: 对每个特征$x_i$引入$k$维的辅助向量$v_i$, 用内积$<v_i, v_j>$代替参数$\omega_{ij}$, 于是从原来的$n(n-1)/2$个参数降低到$nk/2$个参数, 从而降低了训练复杂度.
$$ y(x) = \omega_0 + \sum_{i=1}^n \omega_i x_i + \sum_{i=1}^{n-1} \sum_{j=i+1}^n <v_{i}, v_{j}>x_i x_j $$
对比两者的参数空间:
原来的参数空间: $\{ \omega_{ij} \}_{i<j}$
新的参数空间: $ \{ V = (v_1, v_2, \ldots, v_n)^T \}$, 其中$v_i = (v_{i1}, v_{i2}, \ldots, v_{ik})$
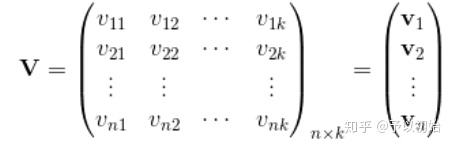
2. 在1.2基础上进一步降低算法复杂度
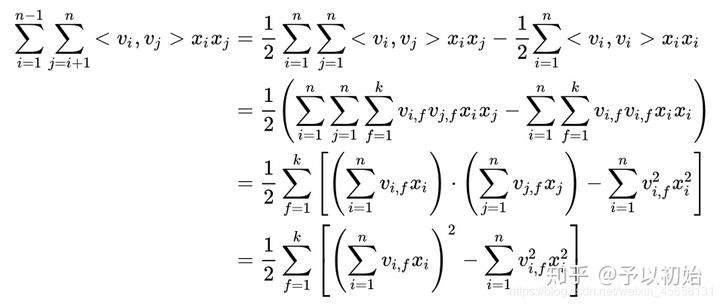
$$ \sum_{i=1}^{n-1} \sum_{j=i+1}^n <v_i, v_j>x_i, x_j = \frac{1}{2} \sum_{i=1}^n\sum_{j=1}^n <v_i, v_j>x_i x_j - \frac{1}{2}\sum_{i=1}^n <v_i,v_i>x_i^2 $$
$$ =\frac{1}{2} ( \sum_i\sum_j\sum_f v_{if}v_{jf} x_i x_j - \sum_i \sum_f v_{if}v_{if} x_i^2 ) $$
$$ =\frac{1}{2} \sum_f[(\sum_{i}v_{if}x_i)(\sum_j v_{jf}x_j) - \sum_{i} v_{if}^2 x_i^2 ] $$
$$ =\frac{1}{2} \sum_f [(\sum_{i}v_{if}x_i)^2 - \sum_{i} v_{if}^2 x_i^2] $$
对需要训练的参数 $\theta$求偏导得:
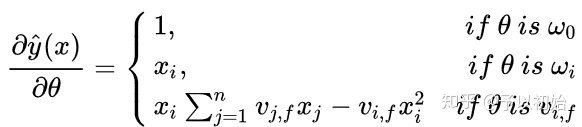
下面固定任一个$v_{if}$ , 考虑其偏导计算的复杂度.
$(v_{if})_{f=1,\ldots,k}$ 表示 特征$x_i$的隐向量,因为梯度项 $\sum_{j=1}^n v_{jf}x_j$ 中不包含$i$ ,只与 $f$ 有关,因此只要一次性求出所有的 $f$ 的 $\sum_{j=1}^n v_{jf}x_j$的值(复杂度 $O(nk)$),在求每个参数的梯度时都可复用该值。
当已知 $ \sum_j v_{jf}x_j$时计算每个参数梯度的复杂度都是 $O(1)$ , 因此训练 FM 模型的复杂度也是 $O(nk)$。[但是总共有nk/2个参数? 注意这里讨论的是单个参数的更新复杂度]
化简之后,FM的复杂度从 $O(n^2 k)$ 降到线性的 $O(nk)$,更利于上线使用.
[FM的复杂度是如何得到的?
观察交叉项的和, 直接对$v_{i,f}$求偏导, 可以发现计算复杂度$O(n^2 k)$]
优缺点总结
优点
考虑了二阶交叉项, 提高了模型表达能力
引入隐向量$v$, 缓解了数据稀疏带来的参数训练难问题
模型复杂度保持为线性, 并且即使改进为高阶特征组合时仍为线性复杂度, 有利于上线应用
缺点
虽然考虑了特征交叉, 但在表达能力上仍不及深度模型
特征$x_i$与其他不同特征组合时的参数贡献都是$v_i$, 但其实在不同特征组合可能有不同的贡献
代码
使用tensorflow, 将FM封装成layer, 随后在搭建model时直接调用即可
model.py - 封装layer
import tensorflow as tf import tensorflow.keras.backend as K class FM_layer(tf.keras.layers.Layer): def __init__(self, k, w_reg, v_reg): super(FM_layer, self).__init__() self.k = k # 隐向量vi的维度 self.w_reg = w_reg # 权重w的正则项系数 self.v_reg = v_reg # 权重v的正则项系数 def build(self, input_shape): # 需要根据input来定义shape的变量,可在build里定义) self.w0 = self.add_weight(name='w0', shape=(1,), # shape:(1,) initializer=tf.zeros_initializer(), trainable=True,) self.w = self.add_weight(name='w', shape=(input_shape[-1], 1), # shape:(n, 1) initializer=tf.random_normal_initializer(), # 初始化方法 trainable=True, # 参数可训练 regularizer=tf.keras.regularizers.l2(self.w_reg)) # 正则化方法 self.v = self.add_weight(name='v', shape=(input_shape[-1], self.k), # shape:(n, k) initializer=tf.random_normal_initializer(), trainable=True, regularizer=tf.keras.regularizers.l2(self.v_reg)) def call(self, inputs, **kwargs): # inputs维度判断,不符合则抛出异常 if K.ndim(inputs) != 2: raise ValueError("Unexpected inputs dimensions %d, expect to be 2 dimensions" % (K.ndim(inputs))) # 线性部分,相当于逻辑回归 linear_part = tf.matmul(inputs, self.w) + self.w0 #shape:(batchsize, 1); batchsize即样本空间大小 # 交叉部分——第一项 inter_part1 = tf.pow(tf.matmul(inputs, self.v), 2) #shape:(batchsize, self.k) # 交叉部分——第二项 inter_part2 = tf.matmul(tf.pow(inputs, 2), tf.pow(self.v, 2)) #shape:(batchsize, k) # 交叉结果 inter_part = 0.5*tf.reduce_sum(inter_part1 - inter_part2, axis=-1, keepdims=True) #shape:(batchsize, 1) # 最终结果 output = linear_part + inter_part return tf.nn.sigmoid(output) #shape:(batchsize, 1) class FM(tf.keras.Model): def __init__(self, k, w_reg=1e-4, v_reg=1e-4): super(FM, self).__init__() # super的用法? self.fm = FM_layer(k, w_reg, v_reg) # 调用写好的FM_layer def call(self, inputs, training=None, mask=None): output = self.fm(inputs) # 输入FM_layer得到输出 return output
utils.py - 预处理数据
# 数据处理代码: import pandas as pd from sklearn.preprocessing import MinMaxScaler from sklearn.model_selection import train_test_split def create_criteo_dataset(file_path, test_size=0.3): data = pd.read_csv(file_path) dense_features = ['I' + str(i) for i in range(1, 14)] # 数值特征 sparse_features = ['C' + str(i) for i in range(1, 27)] # 类别特征 # 缺失值填充 data[dense_features] = data[dense_features].fillna(0) data[sparse_features] = data[sparse_features].fillna('-1') # 归一化(数值特征) data[dense_features] = MinMaxScaler().fit_transform(data[dense_features]) # onehot编码(类别特征) data = pd.get_dummies(data) #数据集划分 X = data.drop(['label'], axis=1).values y = data['label'] X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=test_size) return (X_train, y_train), (X_test, y_test)
train.py - 训练
# 模型训练代码: from model import FM from utils import create_criteo_dataset import tensorflow as tf from tensorflow.keras import optimizers, losses, metrics from sklearn.metrics import accuracy_score, roc_auc_score if __name__ == '__main__': file_path = 'train.txt' # 修改为自己的路径 (X_train, y_train), (X_test, y_test) = create_criteo_dataset(file_path, test_size=0.2) k = 8 w_reg = 1e-5 v_reg = 1e-5 model = FM(k, w_reg, v_reg) optimizer = optimizers.SGD(0.01) summary_writer = tf.summary.create_file_writer('./tensorboard') # tensorboard可视化文件路径 for epoch in range(100): with tf.GradientTape() as tape: # tape是啥? 梯度带, 用于计算梯度 y_pre = model(X_train) # 前馈得到预测值 loss = tf.reduce_mean(losses.binary_crossentropy(y_true=y_train, y_pred=y_pre)) # 与真实值计算loss值; reduce_mean即求均值 print('epoch: {} loss: {}'.format(epoch, loss.numpy())) grad = tape.gradient(loss, model.variables) # 根据loss计算模型参数的梯度; model.variables指权重? optimizer.apply_gradients(grads_and_vars=zip(grad, model.variables)) # 将梯度应用到对应参数上进行更新 # 需要tensorboard记录的变量(不需要可视化可将该模块注释掉) with summary_writer.as_default(): tf.summary.scalar("loss", loss, step=epoch) #评估 pre = model(X_test) pre = [1 if x>0.5 else 0 for x in pre] # 阈值0.5 print("AUC: ", accuracy_score(y_test, pre))
# 如果要计算AUROC pre = model(X_test) print("AUC: ", roc_auc_score(y_test, pre))


 浙公网安备 33010602011771号
浙公网安备 33010602011771号