3. 线性模型
1. 一元线性回归
1.1 原理
1.2 最小二乘估计
基于均方误差最小化来进行模型求解的方法称为“最小二乘法
书中的\((w^*,b^*) =arg min_{(w,b)}\sum_{i=1}^{m}\left(y_{i}-w x_{i}-b\right)^{2}\)就是指求“欧氏距离”最小的w和b
求解w和b其本质上是一个多元函数求最值的问题,更具体点是凸函数求最值的问题
1.3 极大似然估计
用途:估计概率分布的参数值方法
对于离散型(连续型) 随机变量\(X\),假设其概率质量函数为\(P(x;\theta)\)(概率密度函数为\(p(x;\theta)\)),其中0为待估计的参数值(可以有多个)。现有\(x_1,x_2,x_3,...,x_n\)是来自\(X\)的n个独立同分布的样本,它们的联合概率为
其中\(x_1,x_2,x_3,...,x_n\)是已知量,\(\theta\)是未知量,因此以上概率是一个关于\(\theta\)的函数\(L(\theta)\)为样本的似然函数。极大似然估计的直观想法: 使得观测样本出现概率最大的分布就是待求分布,也即使得联合概率(似然函数)$L( \theta) $取到最大值的\(0^*\)即为\(0\)的估计值。
1.4 机器学习三要素
机器学习三要素
1.模型:根据具体问题,确定假设空间
2.策略:根据评价标准确定选取最优模型的策略 (通常会产出一个“损失函数”)
3.算法:求解损失函数
2. 多元线性回归
即得到:
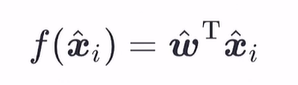


其中,3-9公式的推导:

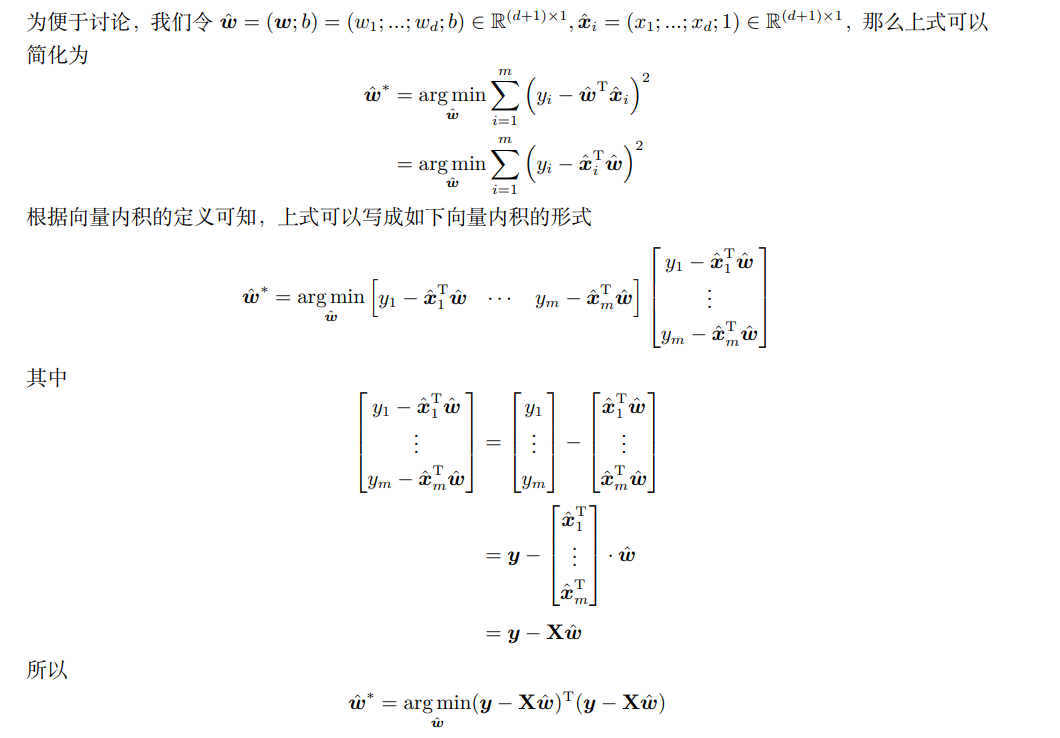
3-10公式的推导:
先将\(E_{\hat{\boldsymbol{w}}}\)展开,再对 $\hat{\boldsymbol{w}} $ 求导可得
由矩阵微分公式 $ \frac{\partial \boldsymbol{a}^{\mathrm{T}} \boldsymbol{x}}{\partial \boldsymbol{x}}=\frac{\partial \boldsymbol{x}^{\mathrm{T}} \boldsymbol{a}}{\partial \boldsymbol{x}}=\boldsymbol{a}, \frac{\partial \boldsymbol{x}^{\mathrm{T}} \mathbf{A} \boldsymbol{x}}{\partial \boldsymbol{x}}=\left(\mathbf{A}+\mathbf{A}^{\mathrm{T}}\right) \boldsymbol{x} $可得
3. 对数线性回归
“对数线性回归”(log-linear regression)实际上是在试图让 \(e^{w^{T}x+b}\)逼近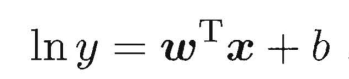 ,在形式上仍是线性回归,但实质上已是在求取输入空间到输出空间的非线性函数映射
,在形式上仍是线性回归,但实质上已是在求取输入空间到输出空间的非线性函数映射
4. 对数几率回归
原理:在线性模型的基础上套一个映射来实现分类功能
此时为一个S型函数,\(y\in[0,1]\)
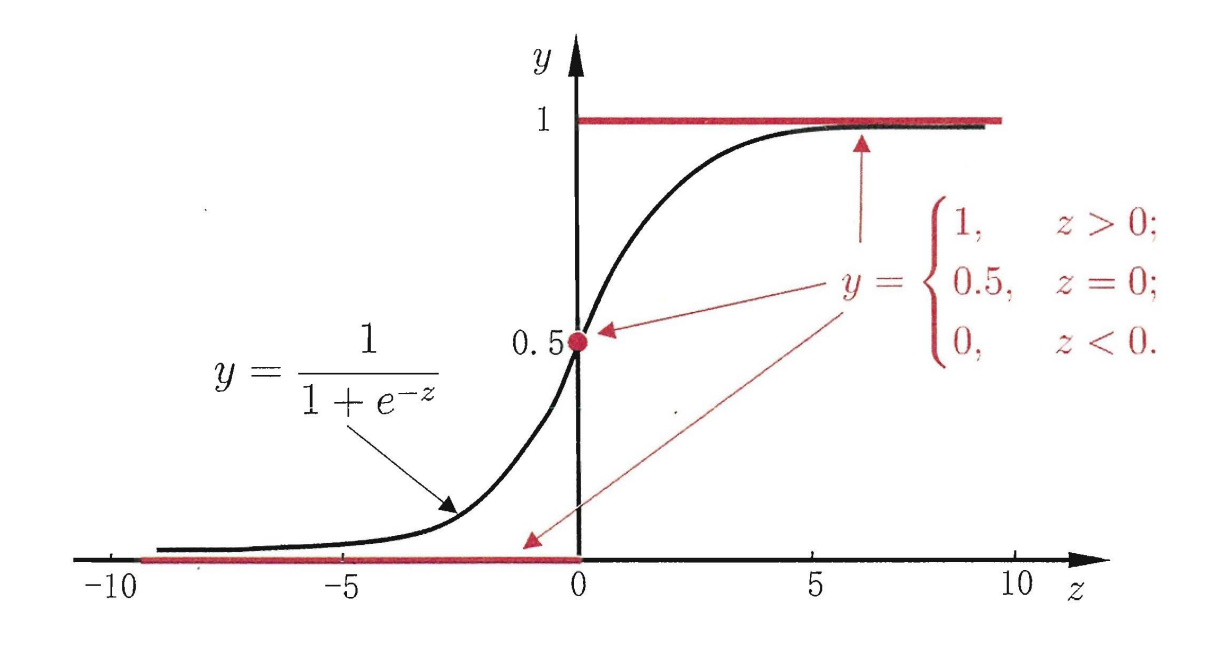


推导得到损失函数:

对数几率回归算法的机器学习三要素
1.模型:线性模型,输出值的范围为[0,1],近似阶跃的单调可微函数
2.策略:极大似然估计,信息论
3.算法:梯度下降,牛顿法
5. 二分类线性判别分析
线性判别分析(Linear Discriminant Analysis,简称 LDA)是一种经典的线性学习方法,在二分类问题上因为最早由[Fisher,1936] 提出,亦称“Fisher 判别分析”
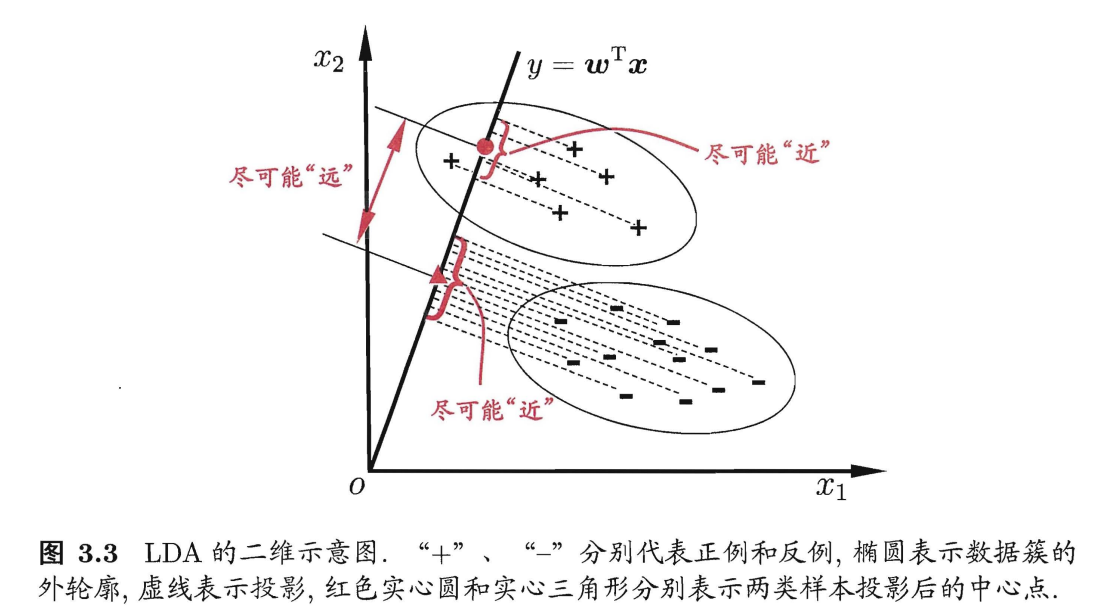
LDA 的思想非常朴素: 给定训练样例集,设法将样例投影到一条直线上使得同类样例的投影点尽可能接近、异类样例的投影点尽可能远离;在对新样本进行分类时,将其投影到同样的这条直线上,再根据投影点的位置来确定新样本的类别。
下图为一个二维示意图:

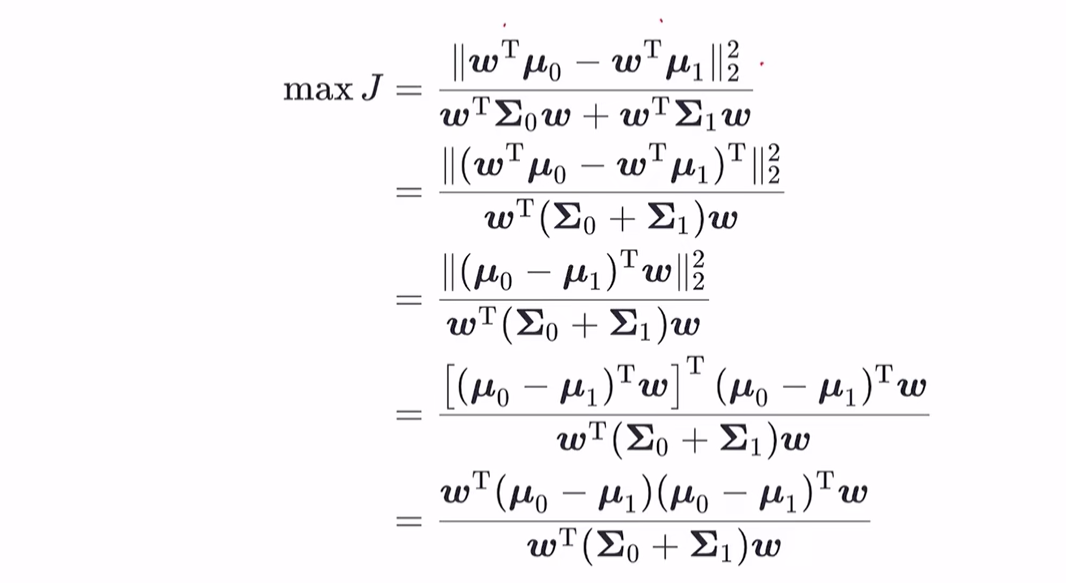
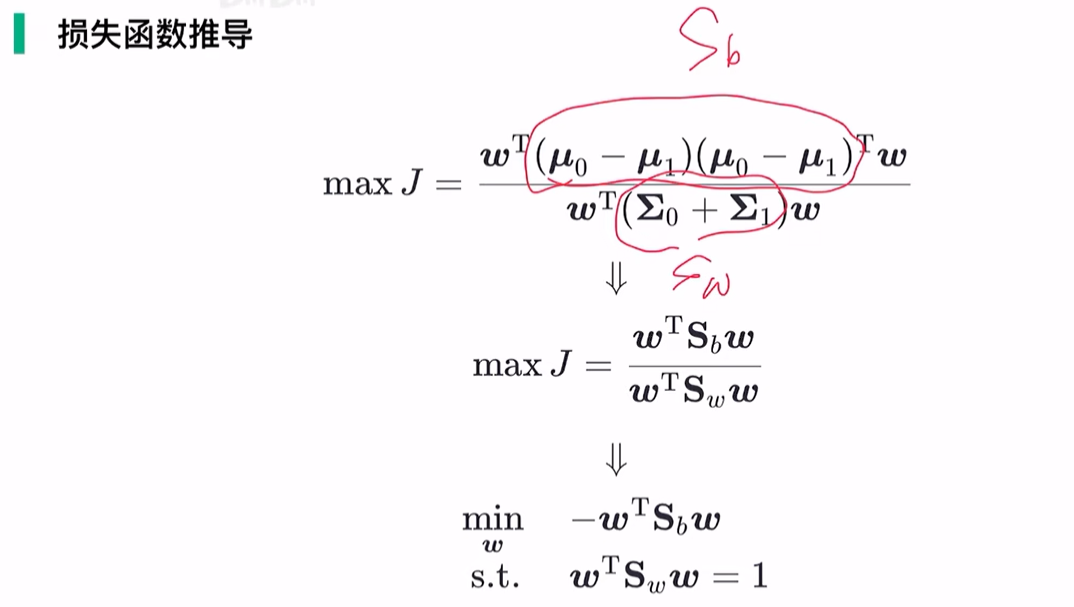



广义瑞利商:





 浙公网安备 33010602011771号
浙公网安备 33010602011771号