2.2数据结构

1.链表

1）单链表：邻接表

 

 数组实现单链表：

#include <iostream>
#include <cstring>
#include <algorithm>
#include <vector>
using namespace std;
const int N = 100010;

//e[N]存储数组
//ne[N]存储每个数的下一个数的下标
//head表示头结点，指向第一个点
//idx表示下一个要存储的点是第idx+1个点
int e[N] , ne[N] , head , idx;

//初始化，head指向空，下一个要输入的是第1个点
void init(){
    head = -1;
    idx = 0;
}
//在链表头处插入值为x的点
void add_to_head(int x){
    e[idx] = x;//在e中存入第idx-1个点为x
    ne[idx] = head;//该点的下一个点为原来的head头结点表示的点
    head = idx;
    idx++;
}
//在第k个插入的点后面插入x
void add(int k , int x){
    e[idx] = x;
    ne[idx] = ne[k];
    ne[k] = idx;
    idx++;
}
//删除第k+2个插入的数
void remove(int k){
    ne[k] = ne[ne[k]];
}

int main()
{
    init();
    int m;
    scanf("%d", &m);
    while (m -- ){
        char r;
        int k,x;
        cin>>r;
        if(r=='H'){
            scanf("%d", &x);
            add_to_head(x);
        }
        else if(r=='D'){
            scanf("%d", &x);
            if(!x) head = ne[head];
            else remove(x-1);
        }
        else{
            scanf("%d%d", &k, &x);
            add(k-1,x);
        }
    }
    for(int i = head ; i!=-1 ; i = ne[i]) cout<<e[i]<<" ";
    cout<<endl;
}

 

2）双链表：优化某些问题

#include <iostream>
using namespace std;
const int N = 100010;
int e[N], r[N] , l[N] ,idx;
int m;
void init(){
    r[0] = 1;
    l[1] = 0;
    idx = 2;
}
void add(int k , int x){
    e[idx] = x;
    l[idx] = k;
    r[idx] = r[k];
    l[r[k]] = idx;
    r[k] = idx;
    idx++;
}
void remove(int k){
    r[l[k]] = r[k];
    l[r[k]] = l[k];
}

int main(){
    init();
    scanf("%d" , &m);
    while(m--){
        int k,x;
        string c;
        cin>>c;
        if(c=="L"){
            scanf("%d" , &x);
            add(0,x);
        }
        else if(c=="R"){
            scanf("%d" , &x);
            add(l[1],x);
        }
        else if(c=="D"){
            scanf("%d" , &k);
            remove(k+1);
        }
        else if(c=="IL"){
            scanf("%d%d" , &k ,&x);
            add(l[k+1],x);
        }
        else{
            scanf("%d%d" , &k ,&x);
            add(k+1,x);
        }
    }
    for(int i = r[0] ; i!=1; i = r[i]) printf("%d " , e[i]);
    return 0;
}

3.模拟栈

#include <iostream>
using namespace std;
const int N = 100010;
int stk[N] , tt ;
void push(int x){
    stk[++tt] = x;
}
void pop(){
    tt--;
}
void empty(){
    if(tt==0) cout<<"YES"<<endl;
    else cout<<"NO"<<endl;
}
void query(){
    cout<<stk[tt]<<endl;
}
int main(){
    int m;
    cin>>m;
    while(m--){
        int x;
        string p;
        cin>>p;
        if(p=="push"){
            scanf("%d" , &x);
            push(x);
        }
        else if(p=="pop"){
            pop();
        }
        else if(p=="empty"){
            empty();
        }
        else{
            query();
        }
    }
    return 0;
}

4.模拟队列

#include <iostream>
using namespace std;
const int N = 100010;
int stk[N] ,ss, tt=-1 ;
void push(int x){
    stk[++tt] = x;
}
void pop(){
    ss++;
}
void empty(){
    if(tt<ss) cout<<"YES"<<endl;
    else cout<<"NO"<<endl;
}
void query(){
    cout<<stk[ss]<<endl;
}
int main(){
    int m;
    cin>>m;
    while(m--){
        int x;
        string p;
        cin>>p;
        if(p=="push"){
            scanf("%d" , &x);
            push(x);
        }
        else if(p=="pop"){
            pop();
        }
        else if(p=="empty"){
            empty();
        }
        else{
            query();
        }
    }
    return 0;
}

5.单调栈

创建一个单调的栈

 

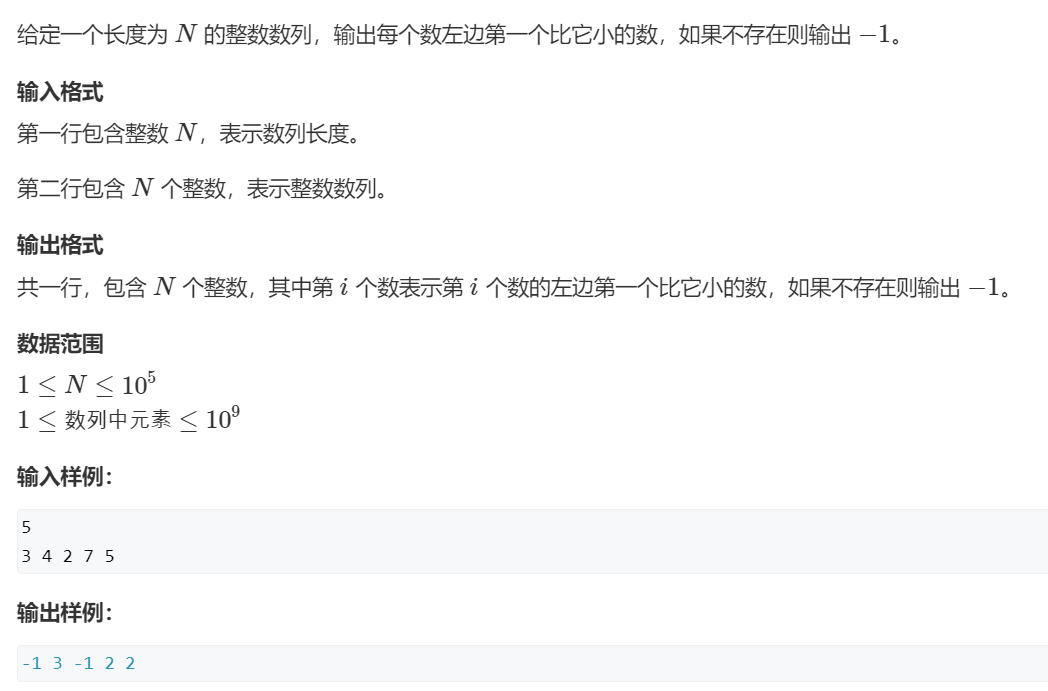
 这题主要是找关系，只要之前存在比后面某数大的数字，这个数就绝对不会再被使用了，我们就得到了一个单调递增的数列

#include <iostream>
using namespace std;
const int N = 100010;
int stk[N] , tt;
int main(){
    int n;
    cin>>n;
    while(n--){
        int x;
        scanf("%d" , &x);
        while(tt and stk[tt]>=x) tt--;
        if(tt==0) cout<<-1<<" ";
        else cout<<stk[tt]<<" ";
        stk[++tt] = x;
    }
    return 0;
}

 6.单调队列（典型题目：滑动窗口）

还是主要是找关系，创建一个单调的数组

（找个样例，实际题目是输出最小和最大）：

 

 代码：

#include <iostream>
using namespace std;
const int N = 1000010;
int a[N] , q[N] ;
int n,k;
int main(){
    scanf("%d%d" , &n, &k);
    for(int i = 0 ; i < n ; i++) scanf("%d" , &a[i]);
    int hh = 0 , tt = -1;//hh是q中存储的最左边的点的下标，tt是q中存储的最右边的点的下标
    for(int i = 0 ; i < n ; i++){
        if(hh<=tt and i-k+1>q[hh]) hh++;//判断是否头部已滑出
        while(hh<=tt and a[q[tt]]>=a[i]) tt--;//删除尾部较大的数
        q[++tt] = i;//读入i
        if(i>=k-1) printf("%d " , a[q[hh]]);//只有i>=k-1才用输出
    }
    cout<<endl;
    hh = 0 , tt = -1;
    for(int i = 0 ; i < n ; i++){
        if(hh<=tt and i-k+1>q[hh]) hh++;
        while(hh<=tt and a[q[tt]]<=a[i]) tt--;
        q[++tt] = i;
        if(i>=k-1) printf("%d " , a[q[hh]]);
    }
    
    return 0;
}

 7.kmp算法

很好的教程地址：https://www.acwing.com/problem/content/discussion/content/1604/

先创建一个next数组，每个下标 i 存放的 j 表示存放每个数之前最大的前 j 个数等于后 j 个数

然后进行 s 数组的遍历

代码：

#include <iostream>
using namespace std;
const int N = 100010 ,M = 1000010;
char s[M] , p[N];
int ne[M] , n , m;
int main(){
    cin>>n>>p+1>>m>>s+1;
    //计算ne数组
    for(int i = 2 , j = 0 ; i <= n ; i++){//一定不要忘了等于
        while(j and p[i]!= p[j+1]) j = ne[j];// 
        if(p[i]==p[j+1]) j++;
        ne[i] = j;
    }
    
    for(int i = 1 , j = 0 ; i <= m ; i++){//也不要忘了等于
        while(j and s[i]!=p[j+1]) j = ne[j];
        if(s[i]==p[j+1]) j++;
        if(j==n) printf("%d " , i-n) , j = ne[j];
    }
    return 0;
}

这个 s + 1 和 p + 1表示从下标是 1 开始读入。