机器学习4- 多元线性回归+Python实现
1 多元线性回归
更一般的情况，数据集 \(D\) 的样本由 \(d\) 个属性描述，此时我们试图学得
\[f(\boldsymbol{x}_i) = \boldsymbol{w}^T\boldsymbol{x}_i+b \text{，使得} f(\boldsymbol{x}_i) \simeq y_i
\]
称为多元线性回归（multivariate linear regression）或多变量线性回归。
类似的，使用最小二乘法估计 \(\boldsymbol{w}\) 和 \(b\)。
由 \(f(\boldsymbol{x}_i) = \boldsymbol{w}^T\boldsymbol{x}_i+b\) 知：
\[f(\boldsymbol{x}_1) = w_1x_{11} + w_2x_{12} + ... + w_dx_{1d} + b \\
f(\boldsymbol{x}_2) = w_1x_{21} + w_2x_{22} + ... + w_dx_{2d} + b \\
... ... \\
f(\boldsymbol{x}_m) = w_1x_{m1} + w_2x_{m2} + ... + w_dx_{md} + b \\
\]
我们记
\[\hat{\boldsymbol{w}} = (\boldsymbol{w};b) = \begin{pmatrix}w_1\\w_2\\ \vdots \\w_d\\b\end{pmatrix}
\]
\[\boldsymbol{X} =\begin{pmatrix}
x_{11} & x_{12} & \cdots & x_{1d} & 1 \\
x_{21} & x_{22} & \cdots & x_{2d} & 1 \\
\vdots & \vdots & \ddots & \vdots & \vdots \\
x_{m1} & x_{m2} & \cdots & x_{md} & 1
\end{pmatrix}
=\begin{pmatrix}
\boldsymbol{x}_1^T & 1 \\
\boldsymbol{x}_2^T & 1 \\
\vdots & \vdots \\
\boldsymbol{x}_m^T & 1
\end{pmatrix}
\]
\[\boldsymbol{y} = (y_1;y_2;\cdots ;y_m) = \begin{pmatrix}y_1\\y_2\\ \vdots \\y_d\end{pmatrix}
\]
可得：
\[\boldsymbol{y} = \boldsymbol{X}\hat{\boldsymbol{w}} \tag{1.1}
\]
类似于前篇博客的式子 (2.3) 有：
\[\hat{\boldsymbol{w}}^* = \underset{\hat{\boldsymbol{w}}}{arg\ min} (\boldsymbol{y} - \boldsymbol{X}\hat{\boldsymbol{w}})^T(\boldsymbol{y} - \boldsymbol{X}\hat{\boldsymbol{w}})
\tag{1.2}
\]
令 \(E_{\hat{\boldsymbol{w}}} = (\boldsymbol{y}-\boldsymbol{X}\hat{\boldsymbol{w}})^T(\boldsymbol{y}-\boldsymbol{X}\hat{\boldsymbol{w}})\)，对 \(\hat{\boldsymbol{w}}\) 求导得：
\[\cfrac{\partial E_{\hat{\boldsymbol w}}}{\partial \hat{\boldsymbol w}}=2\mathbf{X}^T(\mathbf{X}\hat{\boldsymbol w}-\boldsymbol{y})
\tag{1.3}
\]
令上式为零，得到 \(\hat{\boldsymbol{w}}\) 最优解的闭式解。
当 \(\boldsymbol{X}^T\boldsymbol{X}\) 为满秩矩阵（full-rank matrix）或正定矩阵（positive define matrix）时，令式 (1.2) 为零可得：
\[\hat{\boldsymbol{w}}^* = (\boldsymbol{X}^T\boldsymbol{X})^{-1}\boldsymbol{X}^T\boldsymbol{y} \tag{1.4}
\]
令 \(\hat{\boldsymbol{x}_i} = (\boldsymbol{x}_i, 1)\) 得到最终学得的多元线性回归模型为：
\[f(\hat{\boldsymbol{x}}_i) = \hat{\boldsymbol{x}_i}^T(\boldsymbol{X}^T\boldsymbol{X})^{-1}\boldsymbol{X}^T\boldsymbol{y} \tag{1.5}
\]
当 \(\boldsymbol{X}^T\boldsymbol{X}\) 不是满秩矩阵时，可解出多个 \(\hat{\boldsymbol{w}}\) 使得均方误差最小。选择哪个解输出取决于学习算法的归纳偏好。常用做法是引入正则化（regularization）项。
2 多元线性回归的Python实现
现有如下数据，我们希望通过分析披萨的直径、辅料数量与价格的线性关系，来预测披萨的价格：
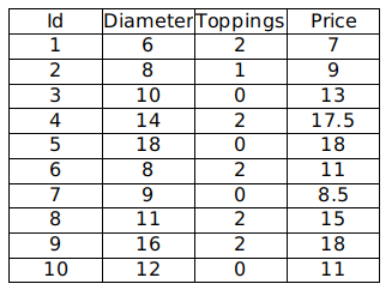
2.1 手动实现
2.1.1 导入必要模块
import numpy as np
import pandas as pd
2.1.2 加载数据
pizza = pd.read_csv("pizza_multi.csv", index_col='Id')
pizza
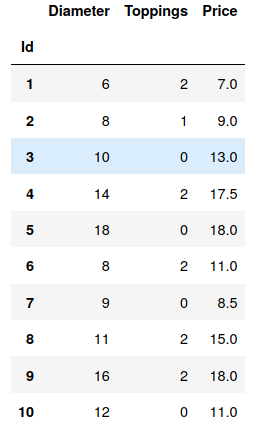
2.1.3 计算系数
由公式
\[\hat{\boldsymbol{w}}^* = (\boldsymbol{X}^T\boldsymbol{X})^{-1}\boldsymbol{X}^T\boldsymbol{y} \tag{2.11}
\]
可计算出 \(\hat{\boldsymbol{w}}^*\) 的值。
我们将后 5 行数据作为测试集，其他为测试集：
X = pizza.iloc[:-5, :2].values
y = pizza.iloc[:-5, 2].values.reshape((-1, 1))
print(X)
print(y)
[[ 6 2]
[ 8 1]
[10 0]
[14 2]
[18 0]]
[[ 7. ]
[ 9. ]
[13. ]
[17.5]
[18. ]]
ones = np.ones(X.shape[0]).reshape(-1,1)
X = np.hstack((X,ones))
X
array([[ 6., 2., 1.],
[ 8., 1., 1.],
[10., 0., 1.],
[14., 2., 1.],
[18., 0., 1.]])
w_ = np.dot(np.dot(np.linalg.inv(np.dot(X.T, X)), X.T), y)
w_
array([[1.01041667],
[0.39583333],
[1.1875 ]])
即：
\[\hat{\boldsymbol{w}}^* = (\boldsymbol{w};b) = \begin{pmatrix}w_1\\w_2\\b\end{pmatrix} = \begin{pmatrix}1.01041667\\0.39583333\\1.1875\end{pmatrix}
\]
\[f(\boldsymbol{x}) = 1.01041667x_1 + 0.39583333x_2 + 1.1875
\]
b = w_[-1]
w = w_[:-1]
print(w)
print(b)
[[1.01041667]
[0.39583333]]
[1.1875]
2.1.4 预测
X_test = pizza.iloc[-5:, :2].values
y_test = pizza.iloc[-5:, 2].values.reshape((-1, 1))
print(X_test)
print(y_test)
[[ 8 2]
[ 9 0]
[11 2]
[16 2]
[12 0]]
[[11. ]
[ 8.5]
[15. ]
[18. ]
[11. ]]
y_pred = np.dot(X_test, w) + b
# y_pred = np.dot(np.hstack((X_test, ones)), w_)
print("目标值：\n", y_test)
print("预测值：\n", y_pred)
目标值：
[[11. ]
[ 8.5]
[15. ]
[18. ]
[11. ]]
预测值：
[[10.0625 ]
[10.28125 ]
[13.09375 ]
[18.14583333]
[13.3125 ]]
2.2 使用 sklearn
import numpy as np
import pandas as pd
from sklearn.linear_model import LinearRegression
# 读取数据
pizza = pd.read_csv("pizza_multi.csv", index_col='Id')
X = pizza.iloc[:-5, :2].values
y = pizza.iloc[:-5, 2].values.reshape((-1, 1))
X_test = pizza.iloc[-5:, :2].values
y_test = pizza.iloc[-5:, 2].values.reshape((-1, 1))
# 线性拟合
model = LinearRegression()
model.fit(X, y)
# 预测
predictions = model.predict(X_test)
for i, prediction in enumerate(predictions):
print('Predicted: %s, Target: %s' % (prediction, y_test[i]))
Predicted: [10.0625], Target: [11.]
Predicted: [10.28125], Target: [8.5]
Predicted: [13.09375], Target: [15.]
Predicted: [18.14583333], Target: [18.]
Predicted: [13.3125], Target: [11.]
# 模型评估
"""
使用 score 方法可以计算 R方
R方的范围为 [0, 1]
R方越接近 1，说明拟合程度越好
"""
print('R-squared: %.2f' % model.score(X_test, y_test))
R-squared: 0.77
此文原创禁止转载，转载文章请联系博主并注明来源和出处，谢谢！
作者: Raina_RLN https://www.cnblogs.com/raina/
