机器学习-2 模拟评估与选择

目录

• 1. 经验误差与过拟合
• 2. 评估方法
  • 2.1 留出法
  • 2.2 交叉验证法
  • 2.3 自助法
  • 2.4 调参
• 3. 性能度量
  • 3.1 错误率与精度
  • 3.2 查准率、查全率与 F1
  • 3.3 ROC 与 AUC
  • 3.4 代价敏感错误率与代价曲线
• 4. 比较检验
  • 4.1 假设检验
  • 4.2 交叉验证 t 检验
  • 4.3 McNemar 检验
  • 4.4 Friedman 检验与 Nemenyi 后续检验
• 5. 偏差与方差

1. 经验误差与过拟合

错误率（error rate）：分类错误的样本数 a 占样本总数 m 的比例，即 \(E = a / m\) 。
精度（accuracy）：精度 = 1 - 错误率 = \(1 - a / m = (1 - \frac{a}{m}) \times 100\%\) （常用百分比形式）。
误差（error）：学习器的实际预测输出与样本真实输出之间的差异。
训练误差（training error）/ 经验误差（empirical error）：学习器在训练集上的误差。
测试误差（testing error）：学习器在测试集上的误差。
泛化误差（generalization error）：学习器在新样本上的误差。

过拟合（overfitting）：将训练样本的自身特性当做了一般性质，在训练集表现很好，在测试集表现糟糕。
解决方法：过拟合是机器学习关键障碍，无法彻底避免，只能“缓解”。
欠拟合（underfitting）：未能学得训练样本的一般性质，在训练集和测试集都表现不好。
解决方法：在决策树学习中扩展分支、在神经网络学习中增加训练轮数等。

模型选择（model selection）问题：现实任务中有多种学习算法可供选择，且同一个学习算法可有不同的参数配置，就出现了选择哪一个学习算法、使用哪一种参数配置问题。
然而，泛化误差无法直接获得，训练误差又存在过拟合问题，所以需考虑使用其他方法进行模型评估。

2. 评估方法

以测试误差作为泛化误差的近似，前提是测试集应尽可能与训练集互斥，即测试样本尽量不在训练集中出现。
从数据集 D 中产生训练集 S 和测试集 T 的常见方法有：留出法、交叉验证法、自助法、参数调节。

2.1 留出法

留出法（hold-out）：直接将数据集 D 划分为两个互斥的集合 S 和 T，即 \(D = S \cup T\)，\(S \cap T = \emptyset\) 。

需注意的是：
S/T 的划分应尽可能保持数据分布的一致性。如：分类任务中可使用分层采样（stratified sampling）保持样本类别的比例相似。
即使在给定 S/T 的样本比例，仍会因不同划分方法产生不同的 S/T，相应的模型评估结果也有差别。所以单次使用留出法不够稳定可靠，一般采用多次随机划分、重复实验评估后取平均值作为最终的评估结果。
若 S 包含绝大多数样本，则训练出的模型更接近用 D 训练出的模型，但由于 T 较小，评估结果可能不够稳定精确；若 T 包含更多样本，则 S 与 D 的差别更大，被评估的模型与用 D 训练出的模型差别较大，降低了评估结果的真实性（fidelity）。常见做法是将大约 2/3 ~ 4/5 的样本用于训练， 剩余样本用于测试，且测试集至少包含 30 个样本。

2.2 交叉验证法

交叉验证法（cross validation）：先将 D 划分成 k 个大小相似的互斥子集，即 \(D = D_1 \cup D_2 \cup ... \cup D_k\) ，\(D_i \cap D_j = \emptyset \quad (i \neq j)\)。每个子集 D_i 都通过分层采样尽可能保持数据分布的一致性。然后，每次使用 k-1 个子集的并集作为训练集，余下子集作为测试集，如此可得到 k 组 训练/测试集，进行 k 次训练和测试，最终返回这 k 个测试结果的均值。

交叉验证法评估结果的稳定性和保真性很大程度上取决于 k 的取值，所以交叉验证法又称为k 折交叉验证（k-fold cross validation）。常用的有 10 折交叉验证、5 折交叉验证、20 折交叉验证等。

将 D 划分成 k 个子集存在多种划分方式，为减小因样本划分不同引入的差别，k 折交叉验证通常要随机使用不同的划分重复 p 次，取这 p 次 k 折线交叉验证结果的均值作为最终的评估结果。常见的有 10 次 10 折交叉验证。

留一法（Leave-One-Out，简称LOO）：假定数据集 D 中包含 m 个样本，令 \(k = m\) 进行交叉验证。
留一法不受随机样本划分方式的影响。留一法中被评估模型与期望评估的用 D 训练得出的模型很相似，因此评估结果往往比较准确。然而，训练集较大时， 计算开销将难以忍受，还是在未考虑算法调参的情况下。另外，留一法的评估结果未必永远比其他评估方法准确，NFL 定理在这里同样适用。

2.3 自助法

在留出法和交叉验证法中，由于保留了一部分样本用于测试，因此必然会引入因训练样本与 D 规模不同而导致估计偏差。而留一法虽受训练样本规模变化的影响较小，但计算复杂度太高。

自助法（boootstrapping）：对数据集 D 使用自助采样（bootstrap sampling）得到采样数据集 D'，将 D' 作为训练集，D - D' （集合减法）作为测试集。
给定包含 m 个样本的数据集 D，对它进行采样产生数据集 D'：每次随机从 D 中挑选一个样本，将其拷贝到 D' 中，然后再该样本放回 D 中，使该样本在下次采样时仍可能被采到。重复执行该过程 m 次，得到包含 m 个样本的数据集 D'，这就是自助采样的结果。

样本在 m 次采样中始终不被采到的概率是 \((1 - \frac{1}{m})^m\)，对其取极限得到：\(\lim\limits_{x\rightarrow\infty}(1 - \frac{1}{m})^m \rightarrow \frac{1}{e} \approx 0.368\)，即通过自助采样，初始数据集 D 中约有 36.8% 的样本没有出现在采样数据集 D' 中。这样，实际评估模型与期望评估的模型都使用 m 个训练样本，而仍有约 1/3 的、没有在训练集中出现的样本用与测试。该测试结果亦称为包外估计（out-of-bag estimate）。

自助法产生的数据集改变了初始数据集的分布，会引入估计偏差，适用于数据集小、难以有效划分训练/测试集的情况。在初始数据量足够的情况下，留出法和交叉验证法更常用。

2.4 调参

参数调节、调参（parameter tuning）：大多数学习算法都有参数需要设定，参数配置不同，学得的模型也可能有显著差别，所以不仅需要选择适用的学习算法，还需要对算法参数进行设定。

由于参数实在实数范围取值，无法对所有参数配置都训练出模型进行挑选，所以常对参数限定一个范围和步长，然后从这些候选值中选择“最佳”的哪个。显然，这样选定的参数往往不是最佳值，但这是在计算开销和性能评估之间折中的结果。即使这样，在不少学习算法中仍然有大量的参数需要设定，参数调得不好，往往对最终模型性能有关键性影响。

给定包含 m 个样本的数据集 D，对模型进行测试评估选定后，学习算法和参数配置也选定了，此时应该用数据集 D 重新训练模型，在这次训练中使用了所有 m 个样本，才是最终的模型。
在评估不同算法的泛化能力时候，我们使用测试集上的效果来估计模型在实际使用时的泛化能力，为了加以区分，我们将训练数据分为训练集和验证集（validation set），使用验证集来进行模型选择和调参。

3. 性能度量

性能度量（performance measure）：衡量模型泛化能力的评价标准。
性能度量反应了任务需求，不同的性能度量会产生不同的评判结果。模型的"好坏"不仅取决于算法和数据，还取决于任务需求。

给定例集 \(D = \{(\vec{x_1}, y_1), (\vec{x_2}, y_2), ..., (\vec{x_m}, y_m)\}\) ，其中 \(y_i\) 是示例 \(\vec{x_i}\) 的 真实标记。要评估学习器 \(f\) 的性能，则需将预测结果 \(f(\mathbf{x})\) 与真实标记 \(y\) 比较。

回归任务常用性能度量是均方误差（mean squared error）:

\[E(f; D) = \frac{1}{m} \sum^m_{i=1}(f(\mathbf{x_i}) - y_i)^2 \tag{3.1} \]

更一般的，对数据分布 \(\mathcal{D}\) 和概率密度函数 \(p(\cdot)\)，均方误差可描述为：

\[E(f; \mathcal{D}) = \int_{\mathbf{x} \sim \mathcal{D}}(f(\mathbf{x}) - y)^2p(\mathbf{x})d\mathbf{x} \tag{3.2} \]

分类任务常用的性能度量有：错误率和精度，查准率、查全率与 F1，ROC 与 AUC，代价敏感错误率与代价曲线。

3.1 错误率与精度

对样例集 \(D\)，分类错误率定义为：

\[E(f;D)=\frac{1}{m}\sum^m_{i=1}\mathbb{I}(f(\mathbf{x_i}) \neq y_i) \tag{3.3} \]

分类任务的精度定义为：

\[\begin{aligned} acc(f;D) &= \frac{1}{m}\sum^m_{i=1}\mathbb{I}(f(\mathbf{x_i}) = y_i) \\ &= 1 - E(f;D) \end{aligned} \tag{3.4} \]

更一般的，对数据分布 \(\mathcal{D}\) 和概率密度函数 \(p(\cdot)\)，分类任务的错误率和精度可分别描述为：

\[E(f;\mathcal{D}) = \int_{\mathbf{x}\sim\mathcal{D}}\mathbb{I}(f(\mathbf{x}) \neq y)p(\mathbf{x})d\mathbf{x} \tag{3.5} \]

\[\begin{aligned} acc(f;\mathcal{D}) &= \int_{\mathbf{x}\sim\mathcal{D}}\mathbb{I}(f(\mathbf{x}) = y)p(\mathbf{x})d\mathbf{x} \\ &= 1 - E(f;\mathcal{D}) \end{aligned} \tag{3.5} \]

3.2 查准率、查全率与 F1

对于二分类问题，将样例根据真实类别与学习器预测类别的组合划分为：真正例（true positive）TP、假正例 （false positive）FP、真反例（true negative）TN、假反例（false negative）FN 四种情况。显然 \(TP + FP + TN + FN = 样本总数\)。分类结果的混淆矩阵（confusion matrix）如下表所示：

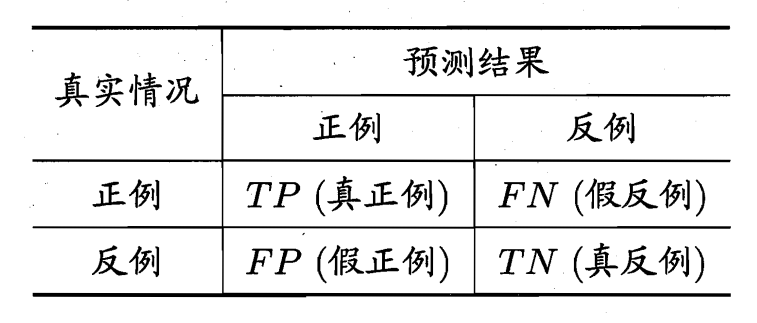
查准率（precision）P 和查全率（recall）R 的定义为：

\[P = \frac{TP}{TP+FP} \tag{3.6} \]

\[R = \frac{TP}{TP+FN} \tag{3.7} \]

查准率：预测出的正例中预测正确的比例。
查全率：所有真实的正例中，有多少比例被正确预测出来。

一般来说，查准率和查全率是一对矛盾的变量。如果希望查准率高，那么只选中最可能是正例的样例，这样查全率就会偏低。而如果希望查全率高，那么选中更多的样本为正例，则查准率又会偏低。

我们将学习器的预测结果对样本进行排序，越可能是正例的排得越靠前，然后从前往后依次作为分界，前面的视为正例，后面的视为反例，然后作出不同分界下的查准率-查全率曲线，简称P-R曲线。如下面的示意图，是不同学习器 A、B、C 的 P-R 曲线：

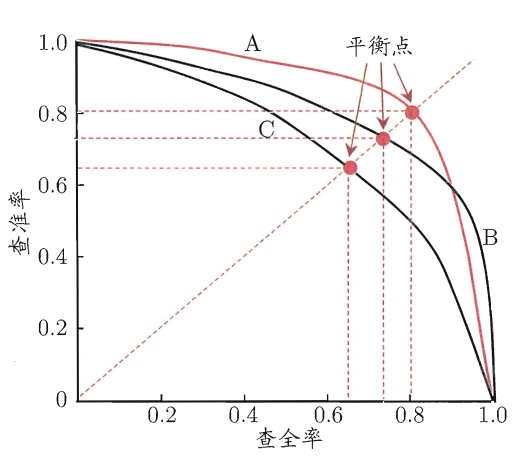
示意图为了绘图方便和美观，为单调平滑曲线，但实际任务中多为非单调、不平滑，且局部有上下波动。

通过 PR 曲线比较不同学习器的性能：

• 若一个学习器的 PR 曲线被另一个学习器的 PR 曲线完全包住，则可断言后者的性能优于前者（如学习器 A 性能优于学习器 C）。

• 若两个学习器的 PR曲线有交叉，则不能笼统地断言孰优孰劣，只能在具体的条件下比较。或通过比较 PR 曲线下面积的大小，面积越大，可认为该学习器在取得查准率和查全率双高的比例更高。

• 比较平衡点。平衡点（Break-Event Point，简称 BEP）是在 \(P = R\) 时的取值。BEP 的值越高，可认为学习器的性能更好。

• 使用 F1 度量。F1 度量是基于查准率和查全率的调和平均（harmonic mean）定义的：

  \[\frac{1}{F1} = \frac{1}{2} \cdot (\frac{1}{P}+ \frac{1}{R}) \]
  \[F1 = \frac{2 \times P \times R}{P + R} = \frac{2 \times TP}{样本总数+TP-TN} \tag{3.8} \]

• 使用 F_β 度量。 F_β 是 F1 的一般形式，为 P 和 R 的加权调和平均：

  \[\frac{1}{F_\beta} = \frac{1}{1+\beta^2} \cdot (\frac{1}{P}+\frac{\beta^2}{R}), \quad (\beta > 0) \]
  \[F_\beta = \frac{(1+\beta^2)\times P\times R}{(\beta^2 \times P)+R}, \quad (\beta > 0) \tag{3.9} \]

  β = 1 时为标准的 F1，β > 1 时查全率更为重要，β < 1 时查准率更为重要。

有时我们希望在多个二分混淆矩阵上综合考察查准率和查全率，例如进行多次训练/测试、在多个数据集上进行训练/测试、在多分类任务中两两类别组合分类……这时可以使用宏查准率（macro-P）、宏查全率（macro-R）、宏F1（macro-F1）、微查准率（micro-P）、微查全率（micro-P）、微F1（micro-F1）。

• 在 n 个混淆矩阵上分别计算出查准率和查全率，记为 \((P_1, R_1), (P_2, R_2), ..., (P_n, R_n)\)，再求平均值，即可得到宏查准率、宏查全率、宏F1：

  \[\text{macro-}P = \frac{1}{n}\sum^n_{i=1}P_i \tag{3.10} \]
  \[\text{macro-}R = \frac{1}{n}\sum^n_{i=1}R_i \tag{3.11} \]
  \[\text{macro-}F1 = \frac{2\times \text{macro-}P\times \text{macro-}R}{\text{macro-}P+\text{macro-}R} \tag{3.12} \]

• 对各混淆矩阵的 TP、FP、TN、FN 求平均值，记为 \(\overline{TP}\)、\(\overline{FP}\)、\(\overline{TN}\)、\(\overline{FN}\)，再基于这些平均值计算微查准率、微查全率、微F1：

  \[\text{micro-}P = \frac{\overline{TP}}{\overline{TP}+\overline{FP}} \tag{3.13} \]
  \[\text{micro-}R = \frac{\overline{TP}}{\overline{TP}+\overline{FN}} \tag{3.14} \]
  \[\text{micro-}F1 = \frac{2\times\text{micro-}P\times\text{micro-}R}{\text{micro-}P+\text{micro}-R} \tag{3.15} \]

3.3 ROC 与 AUC

ROC（Receiver Operating Characteristic，全称受试者工作特性）：将测试样本进行排序，越可能是正例的排在越前面，取不同的预测值作为截断点将样本分为两部分，前面为正例，后面为反例，做出ROC曲线。
ROC曲线的纵轴为真正例率（True Positive Rate，简称 TPR），横轴是假正例率（False Positive Rate，简称 FPR），两者的定义如下：

\[TPR = \frac{TP}{TP+FN} \tag{3.16} \]

\[FPR = \frac{FP}{TN+FP} \tag{3.17} \]

ROC 曲线示意图如下：

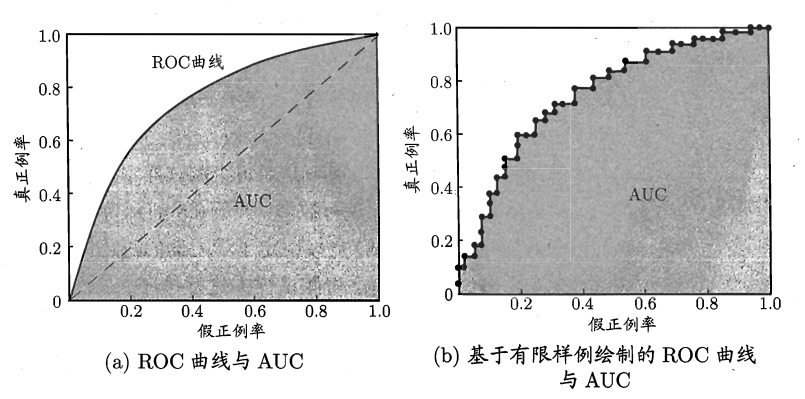
显然 (0,1) 点为所有真实正例排在真实反例前的理想模型。

使用 ROC 曲线比较不同学习器的性能：

• 若一个学习器的 ROC 曲线完全包住另一个学习器的 ROC 曲线，则前者的性能优于后者。

• 比较 AUC（Area Under ROC Curve）：AUC 为 ROC 曲线下的面积。
  假定 ROC 曲线的坐标是 \(\{(x_1,y_1), (x_2,y_2), ...,(x_m, y_m)\}\) 的点按序列简介而成，则 AUC 可估算为：

  \[AUC = \frac{1}{2}\sum^{m-1}_{i=1}(x_{i+1}-x_i)\cdot(y_i + y_{i+1}) \tag{3.18} \]

  AUC 考虑的是样本预测的排序质量，所以它与排序误差关。我们考虑每一对正、反例，若正例的预测值小于反例，则记 1 个罚分，若相等，记 0.5 个罚分，得到排序损失（loss），即 ROC 曲线之上的面积。
  给定 \(m^+\) 个正例和 \(m^-\) 个反例，令 \(D^+\) 和 \(D^-\) 分别表示正、反例集合，则排序损失定义为：

  \[\ell_{rank} = \frac{1}{m^+m^-}\sum_{\boldsymbol{x}^+\in D^+}\sum_{\boldsymbol{x}^-\in D^-}(\mathbb{I}(f(\boldsymbol{x}^+)<f(\boldsymbol{x}^-))+\frac{1}{2}\mathbb{I}(f(\boldsymbol{x}^+))= f(\boldsymbol{x}^-)) \tag{3.19} \]

  且

  \[AUC = 1 -\ell_{rank} \tag{3.20} \]

3.4 代价敏感错误率与代价曲线

现实任务中，不同类型的错误造成的后果可能不同。为权衡不同类型的错误所造成的不同损失，可以使用非均等代价（unequal cost）。

以二分类任务为例，为其设定一个代价矩阵（cost matrix）：

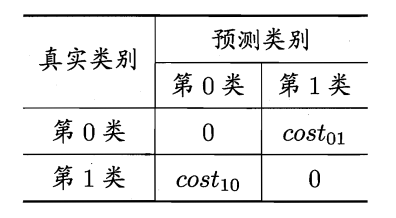
其中 \(\boldsymbol{cost_{ij}}\) 表示第 \(i\) 类样本预测为第 \(j\) 类样本的代价，造成的损失越大，该数值越大。
一般情况下，更关注 \(cost\) 的比值，而非绝对值大小。

若将上表中第 0 类作为正类、第 1 类作为反类，令 \(D^+\) 、 \(D^-\) 分别代表样例集 \(D\) 的正例子集和反例子集，则代价敏感（cost-sensitive）错误率为：

\[E(f;D;cost)=\frac{1}{m}(\sum_{\boldsymbol{x_i}\in D^+}\mathbb{I}(f(\boldsymbol{x_i}) \neq y_i) \times cost_{01} + \sum_{\boldsymbol{x_i}\in D^-}\mathbb{I}(f(\boldsymbol{x_i}) \neq y_i) \times cost_{10}) \tag{3.21} \]

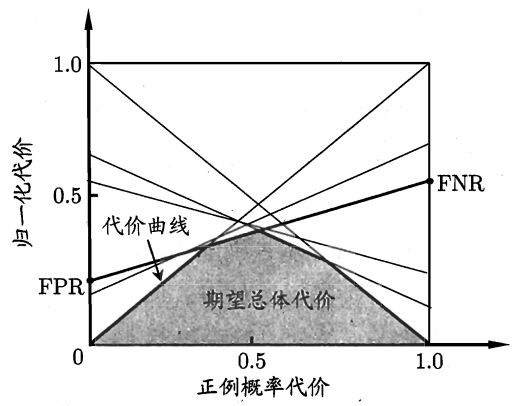
由于在非均等代价在，ROC 曲线不能直接反映学习器的期望总体代价，这时就需要使用代价曲线（cost curve）。
代价曲线的横轴为正例概率代价，纵轴是归一化代价，其定义如下：

\[P(+)cost = \frac{p\times cost_{01}}{p\times cost_{01}+(1-p)\times cost_{10}} \tag{3.22} \]

\[cost_{norm}=\frac{FNR\times p \times cost_{01}+FPR \times (1-p) \times cost_{10}}{p \times cost_{01}+(1-p)\times cost_{10}} \tag{3.23} \]

其中 \(FPR\) 为假正例率，\(FNR = 1-TPR\) 为假反例率，\(p\) 为样例为正例的概率。
代价曲线的横纵轴取值均为 \([0,1]\) 。

代价曲线的绘制（示意图如下）：
ROC 曲线上的每一点都对应代价平面上的一条线段。
设 ROC 曲线上的点坐标为 \((TPR,FPR)\)，则可计算出相应的 \(FNR\) ，然后在代价平面上绘制一条从 \((0,FPR)\) 到 \((1,FNR)\) 的线段。
线段下的面积代表了当前条件下的期望总体代价，当将 ROC 曲线上的每一个点转换为代价平面上的线段后，所有线段的下界围成的面积即为该学习器的期望总体代价。

4. 比较检验

比较学习器的性能不能直接比较某个性能度量的值，因为：

• 通过实验评估方法获得的指数测试集上的性能，并不是真正的泛化性能
• 测试集上的性能与测试集本身的选择有很大的关系，测试集的大小的不同、测试集样例的不同都可能得到不同的结果
• 很多学习算法本身有一定的随机性，即使相同的参数在同一个测试集进行多次测试，结果也可能不同。

假设检测（hypothesis test）可以推断学习器 A 的泛化性能在统计意义上是否优于学习器 B。

下面以错误率为性能度量为例，记错误率为 \(\epsilon\) 。

4.1 假设检验

现实任务中我们无法得到学习器的泛化错误率，只能获知测试错误率 \(\hat{\epsilon}\) ，但是测试错误率不会相差太离谱，所以可以根据测试错误率估推出泛化错误率的分布。

泛化错误率为 \(\epsilon\) 即该学习器在一个样本上犯错的概率为 \(\epsilon\) 。测试错误率 \(\hat{\epsilon}\) 意味着在 \(m\) 个测试样本中有 \(\hat{\epsilon} \times m\) 个样本分类错误。
假定测试样本是从样本总体分布中独立采样得到的，那么泛化错误率为 \(\epsilon\) 的学习器将其中 \(m'\) 个样本错误分类、其余都正确分类的概率是 \(\epsilon^{m'}(1-\epsilon)^{m-m'}\)。则该学习器恰好将 \(\hat{\epsilon} \times m\) 个样本分类错误的概率，即该泛化错误率为 \(\epsilon\) 的学习器在被测试得到的错误率为 \(\hat{\epsilon}\) 的概率为：

\[P(\hat{\epsilon};\epsilon)=\binom{m}{\hat{\epsilon}\times m}\epsilon^{\hat{\epsilon}\times m}(1-\epsilon)^{m-\hat{\epsilon}\times m} \tag{4.1} \]

\(P(\hat{\epsilon};\epsilon)\) 符合二项（binomial）分布，在 \(\epsilon = \hat{\epsilon}\) 时最大， \(|\epsilon - \hat{\epsilon}|\) 增大时 \(P(\hat{\epsilon};\epsilon)\) 减小。
下图为 \(m = 10, \epsilon = 0.3\) 时，测试得到不同误分类样本数的概率示意图：

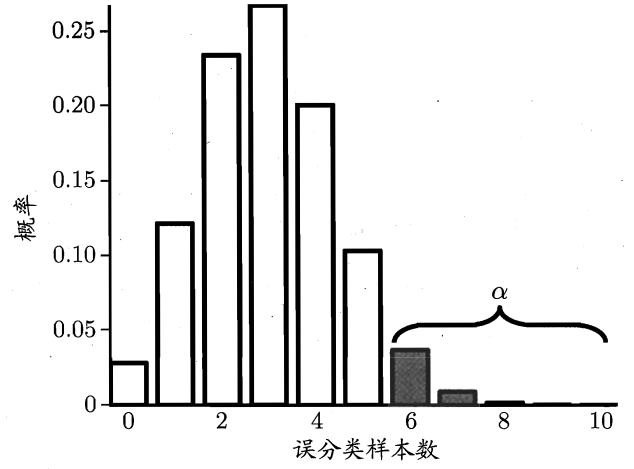
我们使用二项检验（binomial test）对 \(\epsilon \leq \epsilon_0\) 这样的假设进行检验，即泛化错误率是否不大于 \(\epsilon_0\) 。在 \(1-\alpha\) 的概率内所能观测到的最大错误率 \(\overline{\epsilon}\) 计算如下：

\[\overline{\epsilon}=\min \epsilon\quad\text { s.t. } \sum_{i=\epsilon\times m+1}^{m}\left(\begin{array}{c}{m} \\ {i}\end{array}\right) \epsilon_0^{i}(1-\epsilon_0)^{m-i}<\alpha \tag{4.2} \]

s.t 为 subject to 的缩写，即左式在右式条件满足时成立。

若测试错误率 \(\hat{\epsilon}\) 小于临界值 \(\overline{\epsilon}\)，根据二项检验可得：在 \(\alpha\) 的显著度下，假设 \(\epsilon \leq \epsilon_0\) 不能被拒绝，即能以 \(1-\alpha\) 的置信度认为，学习器的泛化错误率不大于 \(\epsilon_0\)；否则该假设可被拒绝，即在 \(\alpha\) 的显著度下可认为学习器的泛化错误率大于 \(\epsilon_0\)。

在测试时我们通常会得到多个测试错误率，此时可用 t 检验（t-test）。假定我们得到了 \(k\) 个测试错误率 \(\hat{\epsilon}_1, \hat{\epsilon}_2, ..., \hat{\epsilon}_k\)，则平均错误率 \(\mu\) 和方差 \(\sigma^2\) 为：

\[\mu = \frac{1}{k}\sum^k_{i=1}\hat{\epsilon}_{i} \tag{4.3} \]

\[\sigma^2 = \frac{1}{k-1}\sum^{k}_{i=1}(\hat{\epsilon}_{i} - \mu)^2 \tag{4.4} \]

这 \(k\) 个测试错误率可看做泛化错误率 \(\epsilon_{0}\) 的独立采样，则变量：

\[\tau_{t} = \frac{\sqrt{k}(\mu - \epsilon_{0})}{\sigma} \tag{4.5} \]

服从自由度为 \(k-1\) 的 \(t\) 分布，如图所示：

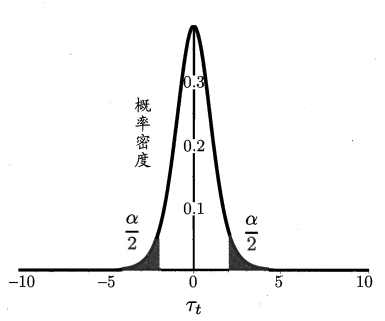
对假设 $ \mu = \epsilon_{0}$ 和显著度 \(\alpha\) ，可计算出当测试错误率均值为 \(\epsilon_{0}\) 时，在 \(1-\alpha\) 概率内能观测到最大错误率，即临界值（考虑双边（two-tailed）假设）。
若 \(|\mu - \epsilon_{0}|\) 位于临界范围 \([t_{-\alpha/2}, t_{\alpha/2}]\) 内，则不能拒绝假设 \(\mu = \epsilon_{0}\)，即泛化错误率为 \(\epsilon_{0}\) ，置信度为 \(1-\alpha\)。
否则可拒绝该假设，即在该显著度下可认为泛化错误率与 \(\epsilon_{0}\) 有显著不同。
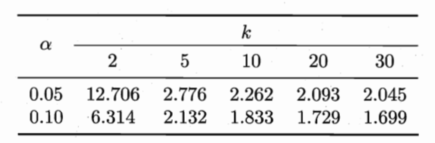
\(\alpha\) 常用取值和常用临界值如下：

上面两种方法是关于单个学习器泛化性能的假设进行检验。对不同的学习器性能的比较可使用下面介绍的假设检验方法。

4.2 交叉验证 t 检验

对两个学习器 A 和 B，使用 \(k\) 折交叉验证法得到的错误率分别为 \(\epsilon^A_1, \epsilon^A_2, ..., \epsilon^A_k\) 和 \(\epsilon^B_1, \epsilon^B_2, ..., \epsilon^B_k\)，其中 \(\epsilon^A_i\) 和 \(\epsilon^B_i\) 为第 \(i\) 折训练/测试集上的结果，可用成对 \(t\) 检验（paired t-test）进行比较检验。
对 \(k\) 折交叉验证法产生的每对测试错误率求差 \(\Delta_i = \epsilon^A_i-\epsilon^B_i\)，若两个学习器性能相同，则差值的均值 \(\mu\) 应为0。
在计算出 \(\Delta_1, \Delta_2, ..., \Delta_k\) 的均值 \(\mu\) 和方差 \(\sigma^2\) 后，在显著度 \(\alpha\) 下，若变量

\[\tau_t = \left|\frac{\sqrt{k}\mu}{\sigma}\right| \tag{4.6} \]

小于临界值 \(t_{\alpha/2,k-1}\) 则假设不能被拒绝，两学习器性能没有显著差别；否则有明显差别，且平均错误率小的性能更优。

\(t_{\alpha/2,k-1}\) 为自由度为 \(k-1\) 的 \(t\) 分布上尾部累积分布为 \(\alpha/2\) 的临界值。

要进行有效的假设检验，需要测试错误率均为泛化错误率的独立采样。但是，在样本有限的情况下，使用交叉验证等方法时，训练集难免有一定程度的重复，造成过高估计假设成立的概率。这时可使用 5×2 交叉验证法。

5×2 交叉验证是做 5 次 2 折交叉验证，每次 2 折交叉验证前将数据打乱，使 5 次交叉验证中数据划分不重复，记学习器 A 和 B 的第 i 次第 k 折交叉验证的测试错误率的差值为 \(\Delta^k_i\)。然后取第一次差值的平均值 \(\mu = 0.5(\Delta^1_1 + \Delta^2_1)\)，再求每 2 折差值的方差 \(\sigma^2_i = (\Delta^1_i - \frac{\Delta^1_i = \Delta^2_i}{2})^2 + (\Delta^2_i - \frac{\Delta^1_i = \Delta^2_i}{2})^2\) 。变量

\[\tau_t = \frac{\mu}{\sqrt{0.2\sum\limits^{5}_{i=1}\sigma^2_i}} \tag{4.7} \]

服从自由度为 5 的 \(t\) 分布，双边检验的临界值为 \(t_(\alpha/2,5)\)，当 \(\alpha = 0.05\) 时为 \(2.5706\)， \(\alpha = 0.1\) 时为 \(2.0150\)。

4.3 McNemar 检验

对二分类问题，使用留出法获得两学习器 A、B 的分类结果的差别，即都正确、都错误、一个正确一个错误的样本数，得到列联表（contingency table）:

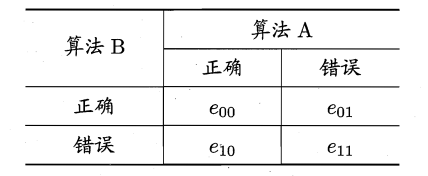
若两学习器性能相同，则应有 \(e_{01} = e_{10}\)，那么 \(\left|e_{01} = e_{10}\right|\) 应服从正态分布，均值为 \(1\)，方差为 \(e_{01} = e_{10}\)。因此变量

\[\tau_{\chi^2} = \frac{(\left|e_{01} - e_{10}\right| - 1)^2}{e_{01} + e_{10}} \tag{4.8} \]

服从自由度为 \(1\) 的 \(\chi^2\)（卡方分布），即标准正态分布变量的平方。给定显著度 \(\alpha\) 当上面变量值小于临界值 \(\chi^2_\alpha\) 时，不能拒绝假设，即两学习器无显著差异；否则拒绝假设，平均错误率较小的学习器性能较优。
自由度为 \(1\) 的 \(\chi^2\) 检验的临界值当 \(\alpha = 0.05\) 时为 \(3.8415\)，\(\alpha = 0.1\) 时为 \(2.7055\)。

4.4 Friedman 检验与 Nemenyi 后续检验

交叉 t 检验和 McNemar 检验只适用与同一数据集上两个学习器性能的比较，若在一组数据集上比较多个算法，可以在每个数据集上使用之前的方法进行两两比较，而更直接的方法是，使用基于算法排序的 Friedman 检验。

假定使用 \(D_1, D2, D3, D4\) 四个数据集对算法 A、B、C 进行比较。
首先得到每个算法下每个数据集上的测试结果，然后在每个数据集上按测试性能由好到坏排序，序值赋 \(1,2,...\)，若性能相同，序值平分，最后对每个算法的序值求平均，得到算法的平均序值，示意表如下：

使用 Friedman 检验，若性能相同，则平均序值应相等。
假定在 \(N\) 个数据集上比较 \(k\) 个算大，\(r_i\) 表示第 \(i\) 个算法的平均序值（为简化，不考虑平分序值情况），则 \(r_i\) 服从均值为 \((k+1)/2\)、方差为 \((k^2-1)/12\) 的正态分布。变量

\[\begin{aligned} \tau_{\chi^2} &= \frac{k-1}{k}\cdot\frac{12N}{k^2-1}\sum_{i=1}^k\Big(r_i - \frac{k+1}{2}\Big)^2 \\ &= \frac{12N}{k(k+1)}\Big(\sum\limits_{i=1}^k r^2_i - \frac{k(k+1)^2}{4}\Big) \end{aligned} \tag{4.9} \]

在 \(k\) 和 \(N\) 都较大时， 服从自由度为 \(k-1\) 的 \(\chi^2\) 分布。

上述的 “原始 Friedman 检验”过于保守，现通常使用变量

\[\tau_F = \frac{(N-1)\tau_{\chi^2}}{N(k-1)-\tau_{\chi^2}} \tag{4.10} \]

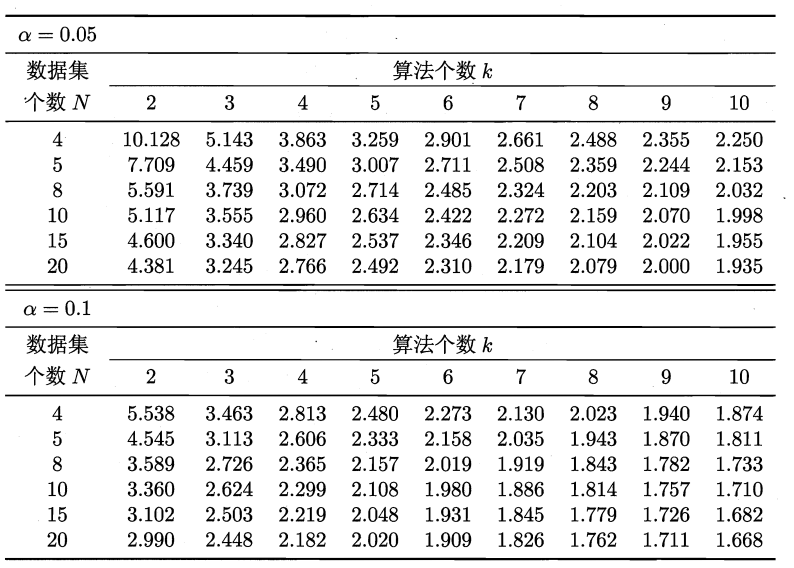
服从自由度为 \(k-1\) 和 \((k-1)(N-1)\) 的 F 分布。下表为 F 检测的常用临界值表：

若“所有算法的性能相同”的假设被拒绝，则需进行后续检验（post-hoc test）区分各算法，常用的有 Nemenyi 后续检验。

Nemenyi 检验计算出平均序值差别的临界值域

\[CD = q_\alpha\sqrt{\frac{k(k+1)}{6N}} \tag{4.11} \]

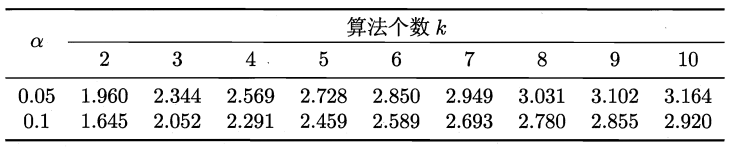
Nemenyi 检验中常用的 \(q_\alpha\) 值如下表：

若两平均序值只差超出临界值 \(CD\)，则说明两算法性能显著不同。

以各算法的平均序值为横轴，各算法为纵轴，用圆点表示平均序值，然后以圆点为中心做横线段代表临界值域的大小，得到 Friedman 检验图，示意图如下：

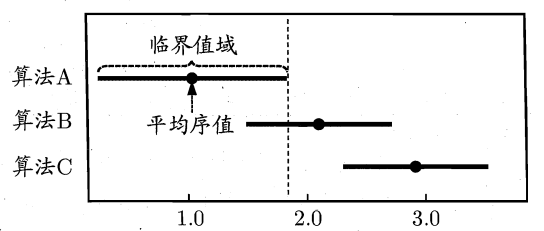
若两算法的横线段有交叠，则两算法无显著区别；否则有显著区别，且平均序值越小，性能越优。

5. 偏差与方差

对学习算法可通过实验估计其泛化性能，偏差-方差分解（bias-variance decomposition）可解释学习算法为什么具有这样的性能。

对测试样本 \(\boldsymbol{x}\)，令 \(y_D\) 为在 \(\boldsymbol{x}\) 在数据集中的标记，\(y\) 为 \(\boldsymbol{x}\) 的真实标记， \(f(\boldsymbol{x};D)\) 为训练集 \(D\) 上学得的模型 \(f\) 在 \(\boldsymbol{x}\) 的预测输出。

以回归任务为例，学习算法的期望预测为：

\[\overline{f}(\boldsymbol{x}) = \mathbb{E}_D[f(\boldsymbol{x};D)] \tag{5.1} \]

使用样本数相同的不同训练集产生的方差为：

\[var(\boldsymbol{x}) = \mathbb{E}_D[(f(\boldsymbol{x};D)-\overline{f}(\boldsymbol{x}))^2] \tag{5.2} \]

噪声为：

\[\varepsilon^2 = \mathbb{E}_D[(y_D-y)^2] \tag{5.3} \]

偏差，即期望输出与真实标记的差别为：

\[bias^2(\boldsymbol{x})=\big(\overline{f}(\boldsymbol{x})-y\big)^2 \tag{5.4} \]

若噪声期望为零，即 \(\mathbb{E}_D[y_D-y]=0\) ，对期望泛化误差进行分解得：

\[\begin{aligned} E(f ; D)=& \mathbb{E}_{D}\left[\left(f(\boldsymbol{x} ; D)-y_{D}\right)^{2}\right] \\ =& \mathbb{E}_{D}\left[\left(f(\boldsymbol{x} ; D)-\bar{f}(\boldsymbol{x})+\bar{f}(\boldsymbol{x})-y_{D}\right)^{2}\right] \\ =& \mathbb{E}_{D}\left[\left(f(\boldsymbol{x} ; D)-\bar{f}(\boldsymbol{x})\right)^{2}\right]+\mathbb{E}_{D}\left[\left(\bar{f}(\boldsymbol{x})-y_{D}\right)^{2}\right] \\ &+\mathbb{E}_{D}\left[2\left(f(\boldsymbol{x} ; D)-\bar{f}(\boldsymbol{x})\right)\left(\bar{f}(\boldsymbol{x})-y_{D}\right)\right] \\ =& \mathbb{E}_{D}\left[\left(f(\boldsymbol{x} ; D)-\bar{f}(\boldsymbol{x})\right)^{2}\right]+\mathbb{E}_{D}\left[\left(\bar{f}(\boldsymbol{x})-y_{D}\right)^{2}\right] \\ =& \mathbb{E}_{D}\left[\left(f(\boldsymbol{x} ; D)-\bar{f}(\boldsymbol{x})\right)^{2}\right]+\mathbb{E}_{D}\left[\left(\bar{f}(\boldsymbol{x})-y+y-y_{D}\right)^{2}\right] \\ =& \mathbb{E}_{D}\left[\left(f(\boldsymbol{x} ; D)-\bar{f}(\boldsymbol{x})\right)^{2}\right]+\mathbb{E}_{D}\left[\left(\bar{f}(\boldsymbol{x})-y\right)^{2}\right]+\mathbb{E}_{D}\left[\left(y-y_{D}\right)^{2}\right]\\ &+2 \mathbb{E}_{D}\left[\left(\bar{f}(\boldsymbol{x})-y\right)\left(y-y_{D}\right)\right]\\ =& \mathbb{E}_{D}\left[\left(f(\boldsymbol{x} ; D)-\bar{f}(\boldsymbol{x})\right)^{2}\right]+\left(\bar{f}(\boldsymbol{x})-y\right)^{2}+\mathbb{E}_{D}\left[\left(y_{D}-y\right)^{2}\right] \end{aligned} \tag{5.5} \]

即泛化误差可分解为偏差、方差和噪声之和：

\[E(f;D) = bias^2(\boldsymbol{x}) + var(\boldsymbol{x}) + \varepsilon^2 \tag{5.6} \]

• 偏差度量了学习算法的期望预测与真实结果的偏离程度，即该学习算法的拟合能力；
• 方差度量了相同大小的训练集的变动所导致的性能的变化，即数据扰动对性能的影响；
• 噪声表达了当前任务上学习算法的期望泛化误差的下界，即学习问题本身的难度。

偏差-方差分解说明了，泛化性能是有学习算法的能力、数据的充分性及学习任务本身的难度共同决定的。

偏差-方差窘境（bias-variance dilemma）：一般偏差和方差是有冲突的，在训练程度不断加深的过程中，先由偏差主导了泛化错误率，而后方差主导泛化错误率，示意图如下：

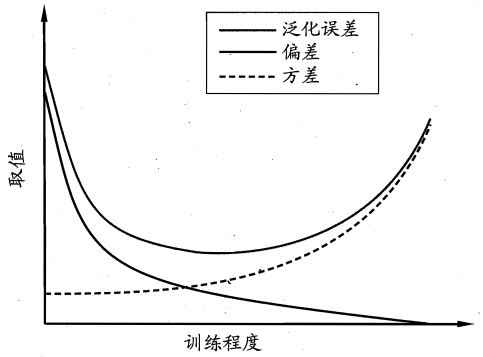
这是由于在训练程度不足时，学习器拟合能力不强，扰动带来的影响不足以带来显著影响；
当学习器拟合能力增强，数据的扰动渐渐能被学习器学到，轻微的扰动也能带来显著变化。