CSP-S模拟35
什么逆天题。
唉呀呀
卸载签免：
话
r摘要，什么**题啊都是， \(T1\) 一点都不显然， \(T2\) 也是一点都不显然，赛时想到了一些但是不会写， \(T3\) 更是不显然的本质不同的 \(border\) 数量， \(T4\) 也是逆天柿子们，反正就是偏离 \(CSP\) 就是了。
还有就是今天下午的歌也是非常之不好听也，像我爸喝多了唱的。
图
另一组图（不是斗罗大陆！！！）
骇
T1 集合——"春风若有怜花意，可否许我再少年。"
喂喂，谁来可怜可怜我！！！
题目描述：
不粘了自己想象。
样例一：
输入：
5 5
1 2
2 3
1 4
4 5
2
3
2
2
4
输出：
3 2 2 3 2
样例二：
输入：
10 10
1 2
2 3
1 4
2 5
2 6
6 7
6 8
2 9
1 10
6
3
6
9
8
4
6
3
8
7
输出：
3 3 1 3 3 3 3 2 3 3
Solve：
首先根据题目文件名，可以想到使用 \(set\) 维护，但是正常的维护是平凡的，只有 \(20pts\) ，于是我们手腕阳历，下图每个节点上的数字们表示按顺序合并后每个节点的“盟友集合”中的元素：
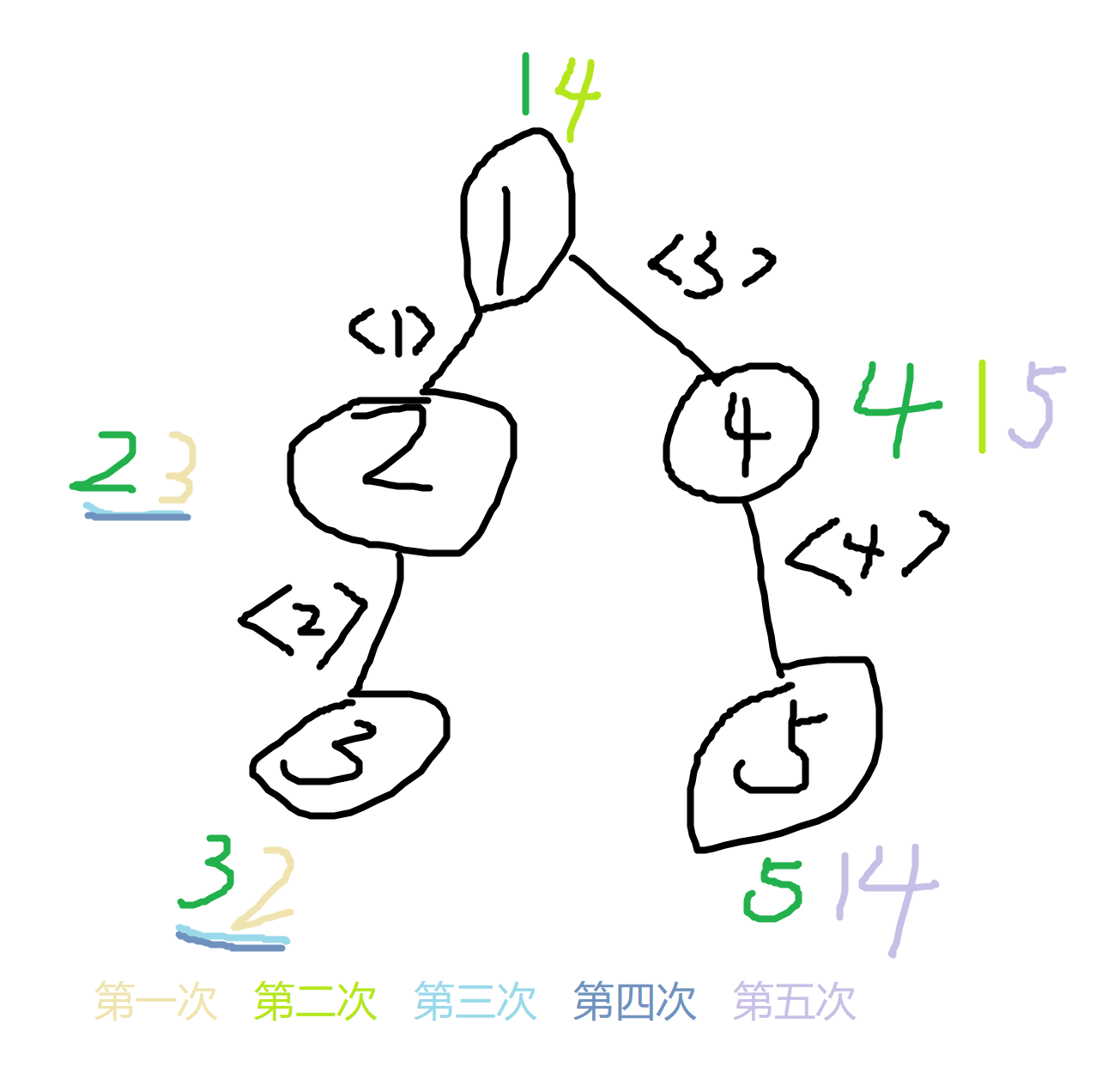
然后我们反着玩一下样例（这里的“第一次”实际上是输入样例的第五次，以此类推）：
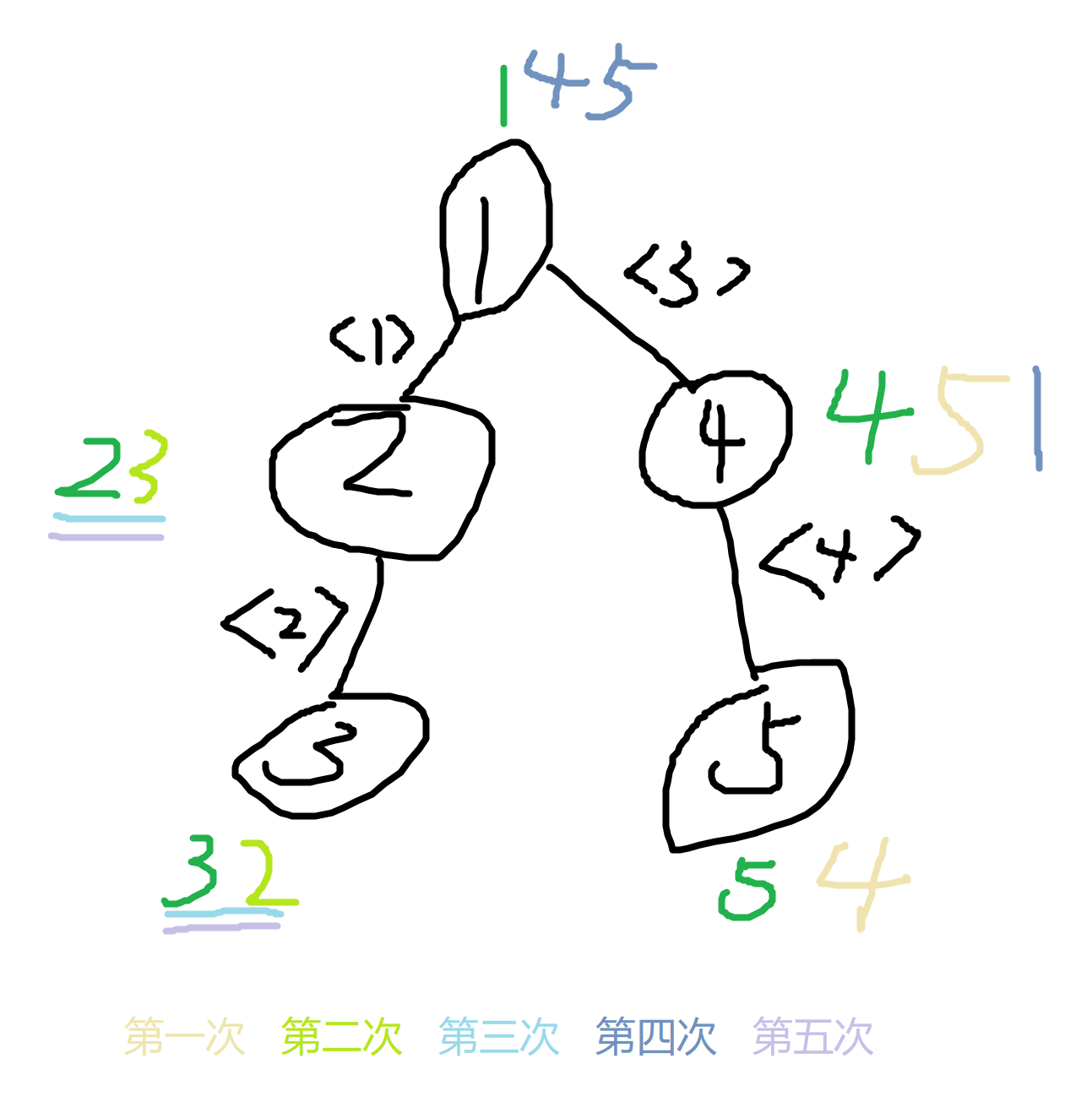
我们惊奇地发现这下面的数字对应着前面那张图每个元素属于的集合编号，比如节点 \(①\) 是属于集合 \(1,4,5\) 的，然后就可以使用 \(bitset\) 反着创优化，如果人聪明常数小，就可以 \(AC\)。
但是为什么？这一点都不显然，我没有那么神秘的注意力，我也不是万能遥控器，对不上脑电波………
于是我们想办法使结论显然化：
点击查看显然
·最初，每个元素都只会存在于与其编号相同的集合；
·第一次合并时，元素 \(2\) 会存在于集合二和集合三中，元素 \(3\) 会存在于集合三和集合二中，我们直接无脑加上就好；
·第二次合并时，元素 \(1\) 会存在于集合一和集合四中，元素 \(4\) 会存在于集合四和集合一中，我们还是直接无脑加上就好；
·第三次合并时，骇，跟第一次一样，于是什么影响都不会有，跳过；
·第四次合并时， \(How~~old~~are~~you~?\) （怎么老是你？），同上；
·第五次合并时，如果平凡地无脑加，那么元素 \(4\) 会存在于集合四、集合一和集合五中，元素 \(5\) 会存在于集合五、集合四和集合一中（¿）我脑子坏了罢，很显然元素 \(5\) 不会出现在集合一中，并且元素 \(1\) 在此时应该被更新为也存在于集合五中口牙，这样的话就很难搞了，我们曾经的操作对后面的操作可能产生影响，可能会乱七八糟判一堆然后假假假假假假假，但是后面的操作不会改变曾经的操作，我们直接反着来就会发现没有这个逆天后效性（肝硬化自己发明的说法）了。
这可能就是 \(OI\) 神犇 \(0.1~ms\) （没那么久!）就能发现的显然了，严谨的证明可能要看鱼鱼的博客（update at 25.10.20 21:34：我*了啊 \(TA\) 博客里啥也没证）。
我们有了从后往前的思路，还需要考虑一件事情：不同时刻对同一条边进行操作时，我们肯定不能直接无脑加（万一这次的操作与上次操作的集合有交那不是坏了吗），于是我们高一选手（高二也是不能忘记了的吧）通过 \(whk\) 数学可得： \(|S\cup T| = |S| + |T| - |S\cap T|\) ，且对于同一条边的两次操作，前一次操作的集合并恰好是后一次操作前的集合交，于是单开个数组记录一下就好，代码比暴力还好写qwq。
Code：
#include <bits/stdc++.h>
using namespace std;
const int _ = 400010;
int n, m, a[_], b[_], x[_], ans[_], h, bfr[_];
bool lian[_];
inline int r(){int x=0,f=1;char ch=getchar();while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch-'0');ch=getchar();}return x*f;}
inline void w(int x){if(x<0)x*=-1,putchar('-');if(x>9)w(x/10);putchar(x%10+'0');return;}
int main(){
freopen("set.in", "r", stdin);
freopen("set.out", "w", stdout);
n = r(), m = r();
for(int i = 1; i < n; i ++){
a[i] = r(), b[i] = r();
ans[i] = 1;
}
ans[n] = 1;
for(int i = 1; i <= m; i ++){
x[i] = r();
}
for(int i = m; i; i --){
h = x[i];
if(! lian[h]){
ans[a[h]] += ans[b[h]];
ans[b[h]] = ans[a[h]];
bfr[h] = ans[a[h]];
lian[h] = 1;
}
else{
ans[a[h]] += ans[b[h]] - bfr[h];
ans[b[h]] = ans[a[h]];
bfr[h] = ans[a[h]];
}
}
for(int i = 1; i <= n; i ++){
w(ans[i]);
putchar(' ');
}
return 0;
}
死
T2 存钱
我也想环游世界。
题目描述：
依旧自己 \(yy\) 。
样例：
输入：
2
3 5 2
2 3 4
6 10 4
2 3 4 5 6 7
输出：
8
16
Solve：
先说赛时罢：
花了 \(inf~~minutes\) 发现样例第二组数据投放·方案的不唯一性，（这其实启发我们可以把最小的随便给扔到边上但是它没注意到）；
·又花了 \(1~ms\) 发现当 \(k = n - 1\) 时，两种钱拼成的长度为 \(m + 1\) 显然更优,并且肝硬化一通乱搞发现当 \(k\) 为 \(n - 2\) 的时候相当于跑两遍 \(n - 1\) ；
但是它什么没想到其他的有助于 \(AC\) 题目的东西；
然后观察样例想到一个逆天假做法就是给输入的东西排个序，每次放当前最短的和最长的，一直放放放放到厌倦，然后自己不相信（幸好没信）给自己又造了一组小样例发现比瞎放还劣，同时意识到当一种钱的数目 \(>m\) 时可以完全不管，并且答案与其取 \(max\) ，然后意识到答案很有可能是不知道几倍的 \((m + 1)\) 减一堆不知道什么的东西 ，之后有想到每次取与前一次钱数量的和最接近 \(m + 1\) 的显然更优，然后就不会实现了（因为柿子只推出一半），罚坐后遗憾离场。
正解：
首先扔掉大于 \(m\) 的 \(a_i\) ，先考虑 \(k = n - 1\) ，如果我们上一个放置的区间的起点在 \(x\) ，现在要放一个长度为 \(y\) 的区间。显然，这个区间的起点应该至少为 \((x + m − 1) − y + 1 + 1 = x + m + 1 − y\) 。我们肯定每次会尽可能往前放置区间。所以总长度应该是 \(∑^n_{i=2}(m + 1 − a_i) + a_n\) ，也
就是 \(m + 1 +∑^{n−1}_{i=2}(m + 1 − a_i)\)，可以将最小的两个数放在 \(1\) 和 \(n\) 。排序一下就可以算出最小答案了（别忘了与最大的 \(a_i\) 取 \(max\)）。
然后考虑 \(k = n − 2\) 。我们将它拆成两个 \(k = n − 1\) ，即将 \(a\) 划分为两个部分，分别跑一遍，最后将两个答案取 \(max\) 。这样做一定是正确的，因为两部分每个部分都最多只完全包含一种钱币。
首先扔掉长度最小的四个区间，它们一定会被放在首尾无贡献。那我们假设全集是 \(U\) ，将区间划分为集合 \(S\) 和集合 \(U − S\)，令 \(cha_i = m + 1 − a_i\) ，那么答案就是 \(m+1+max(∑_{x∈S}cha_x,∑_{x∈U/S}cha_x)\) 。
于是我们可以使用 \(bitset\) 优化 \(0/1\) 背包 \(+\) 随机化大法创过去。
沸羊羊你太粗鲁了！！！
考虑将 \(cha\) 从小到大排序，找到最后一个位置 \(p\) 使得 \(∑^p_{i=1}cha_i ≤ \frac{sum}{2}\) 。
先选上所有 \(p\) 之前的元素，此时的总和与 \(\frac{sum}{2}\) 差值不超过 \(m\)。
如果我们此时进行调整，在总和比 \(\frac{sum}{2}\) 大时去掉 \(p\) 之前选的某个值，在总和比
\(\frac{sum}{2}\) 小的时候加入 \(p\) 之后的某个值，那么我们调整过程中出现的值与 \(\frac{sum}{2}\) 差值都不会超过 \(m\)。
我们从 \(p\) 到 \(n\) 进行调整，加入当前的值或者删除 \(p\) 之前的值。
考虑一个 \(DP\)，设 \(f_{i,j}\) 表示调整到 \(i\) ，要想凑出来 \(j +\frac{sum}{2}\) ，左端点位置的最小值（也就是删除的数都在 \(f_i,j\) 右边）。没有就是 \(0\) 。因为 \(−m ≤ j ≤ m\) 。转移枚举当前值是否加入，在考虑 \(p\) 左侧
新增的能删值是否删除。可以滚动数组。由于每个数在每个 \(j\) 下只会被考虑一次是否加入删除，所以时间复杂度 \(O(nm)\)，人聪明常数小。
实现上，下标肯定不能是负的（大蛇爱用用 \(map\) 当我没说），需要将数组下标整体加上 \(10000\) （数据范围是一万）。
code：
#include<bits/stdc++.h>
using namespace std;
const int _ = 20010;
int t, n, m, tot, k, x, y, mx, a[_], b[_], cha[_], f[_], g[_], as, ans, all;
signed main(){
freopen("money.in", "r", stdin);
freopen("money.out", "w", stdout);
scanf("%d", & t);
while(t --){
all = as = ans = 0;
for(int i = 0; i <= 20000; i ++){
f[i] = g[i] = 0;
}
scanf("%d%d%d", & n, & m, & k);
tot = 0;
bool yes = (k == n - 1);
for(int i = 1; i <= n; i ++){
cin >> a[i];
}
sort(a + 1, a + 1 + n);
mx = a[n];
if(a[1] > m){
printf("%d\n", mx);
continue;
}
n = lower_bound(a + 1, a + n + 1, m + 1) - a - 1;
if(yes){
ans = m + 1;
for(int i = 3; i <= n; i ++){
ans += m + 1 - a[i];
}
printf("%d\n", max(ans, mx));
continue;
}
if(n <= 2){
printf("%d\n", mx);
continue;
}
if(n <= 4){
printf("%d\n", max(mx, m + 1));
continue;
}
for(int i = 5; i <= n; i ++){
cha[++ tot] = m + 1 - a[i];
}
n = tot;
sort(cha + 1, cha + 1 + n);
for(int i = 1; i <= n; i ++){
all += cha[i];
}
int p = 1, sum = 0;
for(; p <= n && sum + cha[p] <= (all >> 1); p ++){
sum += cha[p];
}
g[sum - (all >> 1) + 10000] = p;
for(int i = p; i <= n; i ++){
for(int j = 0; j <= 20000; j ++){
f[j] = g[j];
}
for(int j = 0; j <= 9999; j ++){
f[j + cha[i]] = max(f[j + cha[i]],g[j]);
}
for(int j = (10000 << 1); j >= 10001; j --){
for(int tot = g[j]; tot < f[j]; tot ++){
f[j - cha[tot]] = max(f[j - cha[tot]], tot);
}
}
for(int j = 0; j <= 20000; j ++){
g[j] = f[j];
}
}
for(int i = 10000; i >= 0; i --){
if(f[i]){
as = (all >> 1) - 10000 + i;
break;
}
}
printf("%d\n", max(mx, m + 1 + all - as));
}
}
我
T3 串串
说道手机，我前两天刚把旧手机………不对好像串台了那是转转【大雾】。
力
T4 游走
神级游走NPC。
浙公网安备 33010602011771号