CSP-S模拟29——《霸道式子碍上我，怠懵蒟蒻哪里逃》

写在前面：

~~可爱可怜的SKK学长%%%~~

$RT$， $_{OI}^{HZ}$ 进入大数学时代。

推歌：

《苍蝇》

猫可爱狗可爱
全世界我最不可爱
春暖花开你不期待
但我还是会回来回来
什么仇什么怨
毁灭我与我不相干
你说因为你讨厌
但我只是想唱唱歌
我是病菌你家就是我家
搓搓我的前爪自己拿
我是命运落在你的下巴
给你一个嘴巴自己打
我是苍蝇是卑劣的优雅
收集这世界的背面的残渣
啦啦啦啦啦
以肮脏的名义把世界净化
拿起武器
压倒性的辉煌的实力
挥
你胜利我死去
我在我尸体上站起站起
人类缺乏情趣
把决斗幸存当胜利
胜利当作正义
把正义当上帝
过度攫取占有欲
去掠夺然后再舍弃
制造垃圾消费意义
两败俱伤的胜利胜利
他带着荣耀死去
灵魂到天堂或地狱
但我哪儿也不去
我留在这里唱唱歌
我是轮回翻飞我的翻飞
偷窥所有长夜的喜悲
你是人类以为你的以为
你猜你的上帝更爱谁
我是苍蝇是黑色的标点
整理这世界前后的章节
啦啦啦啦啦
在王冠的下面看英雄熄灭
我是病菌是命运是轮回
是翻飞的黑色的世界的标点
你是自称人类的谁
我是病菌你家就是我家
搓搓我的前爪自己拿
我是命运落在你的下巴
给你一个嘴巴自己打
我是苍蝇是卑劣的优雅
收集这世界的背后的残渣
啦啦啦啦啦
以肮脏的名义把世界净化

废话

好讨厌好讨厌好讨厌好多好多好多恐怖诡异逆天的 $ex$ 柿子！！！机房打捞讲得都非常不言而喻一目了然但是肝硬化这位可悲可泣的蒟蒻还是依旧地不会口牙！ $T1$ 赛时想到了一小部分，但没想出来，打的表现在（2025年10月11日20:02:12）还没跑出来，于是爆零； $T2$ 想容斥，假了半年，于是打的暴力 $16~pts$ ； $T3$ 也是成功没看懂——我的样例都没玩出来； $T4$ 暴力打假了， $5~pts$ 遗憾离场。最终 $0~+~16~+~0~+~5~=~21pts$ 结束了肝硬化的悲惨一生上午。

I

T1 一个赢家

~~我输了，你让让我。~~

题目描述：

样例1:

输入：

输出：

666666672

样例2:

输入：

输出：

977296785

样例3:

输入：

输出：

321812306

样例4:

输入：

输出：

226302763

数据范围：

$1≤n≤5~×~10^6$ 。

Solve：

《最绝望》

其实没看懂，
柿子到底怎么推，
无脑往上霍。

首先我们众所周知概率肯定是一个小于等于 $1$ 的分数，但是样例的答案非常非常大，这个时候是个活人就可以想到用逆元，但是式子怎么推呢？

\[我不会 \]

但是我们有题解：

~~碰碰。~~（by：Wy_x学长）

Code:

柿子没推出来不好意思粘代码（其实代码非常好写）。

Have

T2:储蓄计划之缘千里排列计数（count）

~~别样的错题/重题/难题大比拼.~~

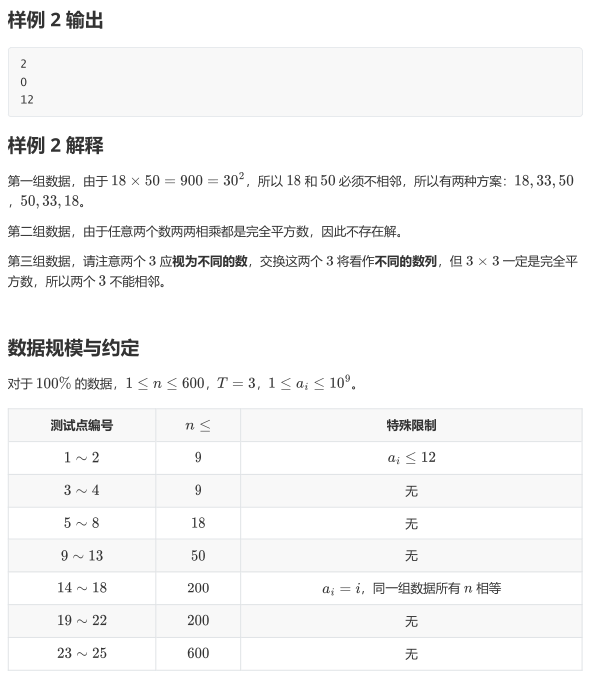
Solve:

其实没看懂题解。
感谢SKK大蛇学长的讲解&鱼鱼长老的博客，使我茅厕蹲开。
可以通过实践发现无脑暴搜可以得到 $16pts$ 的大众分（甚至绝对众数¿）；
于是考虑正解，~~因为不会部分分。~~
-首先考虑对 $a_i$ 进行预处理，若它的一个质因子出现了偶数次，则这个质因子不能对答案产生影响，于是直接删去。
-是的，这很显然。
-于是问题就变成了求一个序列中相邻两个元素均不相等的方案数。
-等等等等等一下这一点都不显然凭什么是这样的？！
-可以发现，如果有两个数 $x$ , $y$ ，其中

$x~=~p_1^{2a-1}~·~p_2^{2b}~·~p_3^{2c-1}~·~p_4^{2d}$ ，

$y~=~p_3^{2a-1}~·~p_4^{2b}~·~p_5^{2c-1}~·~p_6^{2d}$ ，

所以
$x~·~y~=~p_1^{2a-1}~·~p_2^{2b}~·~p_3^{2(a+c-1)}~·~p_4^{2(d+b)}~·~p_5^{2c-1}~·~p_6^{2d}$ ，

存在质因数不为偶次幂，不是完全平方数；
预处理后的 $x~=~p_1^{1}·p_3^{1}$ ， $y~=~p_3^{1}·p_5^{1}$ ，两数有不同的质因子，不相同；

再设两个数 $m$ ， $n$ ，其中

$m~=~p_1^{2a}~·~p_2^{2b}~·~p_3^{2c-1}~·~p_4^{2d-1}$ ，

$n~=~p_3^{2a-1}~·~p_4^{2b-1}~·~p_5^{2c}~·~p_6^{2d}$ ，

$m~·~n~=~p_1^{2a}~·~p_2^{2b}~·~p_3^{2(a+c)}~·~p_4^{2(d+b)}~·~p_5^{2c}~·~p_6^{2d}$ ，

所有质因数都为偶次幂，是完全平方数；
预处理后的 $m~=~p_3^{1}~·~p_4^{1}$ ， $n~=~p_3^{1}~·~p_4^{1}$ ，两数没有不同的质因子，是相同的。

问题就转化成功了。

于是开始考虑 $DP$ 怎么写。
钦定 $f_{i,j}$ 为前 $i$ 种元素组成的序列中，有 $j$ 对数是不合法（两数乘积为完全平方数）的方案数，
由于编号不同但大小相同的两个数交换位置为不同的方案，于是答案为 $$f_{num，0}·\prod_{i=1}^{num}cnt_i!$$ ，其中 $num$ 为元素种类数， $cnt_i$ 为每种元素出现的次数。

现在考虑如何转移：
钦定 $h$ 为第 $i$ 种元素出现的次数，它们可以有两种不同的放法：
1.放到与其相等的元素旁边。（于是这个序列就坏上加坏了（相邻两数之积为完全平方数的对数增加），每这样放入 $x$ 个元素，就会使 $f$ 第二维 $+x$ ）
2.放到与其不等的元素旁边。（可能会使原本的序列变好（相邻两数之积为完全平方数的对数减少），也可能不变）
设按方法 $1$ 放入的元素个数为 $x$ ，方法 $2$ 为 $y$ ， $p$ 为方法二让序列变好的部分， $q$ 为方法二剩下部分，于是转移方程为：

\[f_{i+1,j-p+x}~+=~f_{i,j}~*~\binom{h-1}{y-1}~*~\binom{j}{p}~*~\binom{sum+1-j}{q} \]

其中 $sum$ 为前 $i$ 种元素的总个数。
在实现上，可以使用离散化来存储预处理后的数，但是肝硬化很懒，于是用的 $map$ 。

Code：

#include <bits/stdc++.h>
const int _ = 606, mod = 1e9 + 7;
int n, a[_], t, h;
long long dp[_][_], c[_][_], jc[_], ans, sum;
std::map<int, int> mp;
inline int shan(int x){
	for(int i = 2; i * i <= x; i ++){
		while(x % (i * i) == 0){
			x /= i * i;
		}
	}
	return x;
}
int main(){
	freopen("count.in", "r", stdin);
	freopen("count.out", "w", stdout);
	for(int i = 0; i <= 600; i ++){
		c[i][0] = c[i][i] = 1;
		for(int j = 1; j < i; j ++){
			c[i][j] = (c[i - 1][j - 1] + c[i - 1][j]) % mod;
		}
	}
	jc[0] = 1;
	for(int i = 1; i <= 600; i ++){
		jc[i] = (jc[i - 1] * i) % mod;;
	}
	scanf("%d", & t);
while(t --){
	scanf("%d", & n);
	std::memset(dp, 0, sizeof(dp));
	dp[1][0] = 1;
	sum = 0;
	mp. clear();
	for(int i = 1; i <= n; i ++){
		scanf("%d", & a[i]);
		a[i] = shan(a[i]);
		mp[a[i]] ++;
	}
	int i = 1;
	for(auto hh : mp){
		h = hh. second;
		for(int j = 0; j <= sum; j ++){
			if(dp[i][j]){
				for(int k = 0; k < h; k ++){
					for(int l = 0; l <= std::min(j, h - k); l ++){
						int m = j - l + k;
						dp[i + 1][m] = (dp[i + 1][m] + dp[i][j] * c[h - 1][h - k - 1] % mod * c[j][l] % mod * c[sum + 1 - j][h - k - l] % mod) % mod;
					}
				}
			}
		}
		sum += h;
		i ++;
	}
	ans = dp[i][0];
	for(auto h : mp){
		ans = (ans * jc[h. second]) % mod;
	}
	printf("%lld\n", ans);
}
	return 0;
}

No

T3 树上染黑

~~看不懂直接 $CE$ 了。~~

题目描述:

$n$ 个结点的树，对每个结点设为根求：枚举剩下 $n-1$ 个结点的顺序（ $a_1, \cdots, a_{n-1}$ ）并求和：初始只有根为黑色，从 $1$ 到 $n-1$ 枚举 $i$ ，将 $a_i$ 到根的路径染黑，并把黑色结点数加入答案，对 $998244353$ 取模。

输入格式:

第一行一个正整数 $n$ ，表示点数。接下来 $n-1$ 行，每行两个正整数 $u_i, v_i$ ，表示 $u_i, v_i$ 之间有一条边。保证给出的边形成一棵树。

输出格式：

$n$ 行，第 $i$ 行输出节点 $i$ 为根时的答案。

Solve：

其实赛时我没看懂题是什么意思，但是赛后经过机房打捞の讲解，终于…看懂了题面。于是还是不会，但是我们知道题意就是 $n$ 个结点的排列，对虚树大小求和。
记 $f(u,A)$ 为节点 $u$ 到点集 $A$ 的虚树的距离，其中 $a_0=u,a_0,\cdots,a_{n-1}$ 为长度为 $n$ 的排列。
于是可以得出答案为：~~（之后式子全是霍的）~~

\[ans_u=(n-1)(n-1)!+\sum_{a_i}\sum_{i=1}^{n-1}(n-i)f(a_i,\begin{Bmatrix}a_0,\cdots,a_i-1\end{Bmatrix}) \]

\[=(n-1)(n-1)!+\sum_{v \ne u}\sum_{i=1}^{n-1}(n-i)\sum_{|A|=i,u \in A}f(v,A)(i-1)!(n-i-1)! \]

\[=(n-1)(n-1)!+\sum_{v \ne u}\sum_{i=1}^{n-1}(n-i)!(i-1)!\sum_{|A|=i,u \in A}\sum_{w \in anc_v}\begin{bmatrix}Subtree(w) \cap A= \varnothing \end{bmatrix} \]

\[=(n-1)(n-1)!+\sum_{v \ne u}\sum_{i=1}^{n-1}(n-i)!(i-1)!\sum_{w \in anc_v}\binom{n-1-siz_w}{i-1} \]

\[=(n-1)(n-1)!+\sum_{a_i}\sum_{i=1}^{n-1}(n-i)!(i-1)!\sum_{|A|=i,u \in A}\binom{n-1-siz_w}{i-1}siz_w \]

Egg

T4 摆放花盆

~~逆天数据结构不似活人我不会。~~

I Have No Egg!!!!111

posted @ 2025-10-11 22:05 养鸡大户肝硬化阅读(28) 评论(4) 收藏举报

刷新页面返回顶部

rain20100708

CSP-S模拟29——《霸道式子碍上我，怠懵蒟蒻哪里逃》

写在前面：

《苍蝇》

I

T1 一个赢家

题目描述：

样例1:

输入：

输出：

样例2:

输入：

输出：

样例3:

输入：

输出：

样例4:

输入：

输出：

数据范围：

Solve：

Code:

Have

T2:储蓄计划之缘千里排列计数（count）

Solve:

Code：

No

T3 树上染黑

题目描述:

输入格式:

输出格式：

Solve：

Egg

T4 摆放花盆

I Have No Egg!!!!111

公告

rain20100708

CSP-S模拟29——《霸道式子碍上我，怠懵蒟蒻哪里逃》

写在前面：

《苍蝇》

I

T1 一个赢家

题目描述：

样例1:

输入：

输出：

样例2:

输入：

输出：

样例3:

输入：

输出：

样例4:

输入：

输出：

数据范围：

Solve：

Code:

Have

T2:储蓄计划 之缘千里 排列计数（count）

Solve:

Code：

No

T3 树上染黑

题目描述:

输入格式:

输出格式：

Solve：

Egg

T4 摆放花盆

I Have No Egg!!!!111

公告

T2:储蓄计划之缘千里排列计数（count）