二叉树的性质

性质1：  在二叉树的第 i 层至多有2^( i - 1)个节点   ，至少有 1 个节点                             （ 度：节点拥有的子节点的个数 ）

性质2： 在深度为 k 的二叉树中，至多有2^k -1个节点 ，至少有 k 个节点

性质3： 对任何一颗二叉树，叶子个数为 n0 ，度数为 2 的节点个数为 n2 ；则 n0 = n2 + 1 ；

 

性质4，具有 n 个节点的完全二叉树的深度为 

 

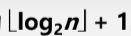
性质5： 如果对一颗有n个节点的完全二叉树，按层序编号，每层从左到右，则对任意一个节点 i ，有：

             1）如果 i =1，则 i 是二叉树的根，无双亲结点； 如果 i >1，则其双亲结点为 

  

             2） 如果 2i > n，则该节点为叶子节点；无左孩子，否则，其左孩子为 2i 

             3） 如果 2i+1>n ，则此节点无右孩子；否则其右孩子为 2i+1 

            此条性质说明了完全二叉树中，双亲结点编号与孩子节点编号之间的关系；

 

练习

一个有n个节点的二叉树中，有  n+1 个空指针域；，

每个节点都有两条链，所以一共有2n 条链，而除了根节点外每个节点都只有一个双亲，即上部只有一条链子（去除指向非空的指针域）

所以， 如果有n个节点，那么就有 2n - ( n -1) = n +1 个空指针域；