单调队列

单调队列

单调队列，顾名思义，就是在队列的基础上，维护一个单调的序列。

性质

1. 队列中的元素其对应在原来的序列中的顺序必须是单调递增的。
2. 队列中元素的大小必须是单调递(增/减/自定义)。

回到上面的单调队列问题，假如你在饭堂打饭时，有个人人高马大，急匆匆跑过来，看排了这么一长串队，心中急躁，从队列最后的一个人开始，看见好欺负的就赶走，自己站着，直到干不过的就停下，这就是双端队列。也就是允许两端弹出，只允许一端插入的队列（允许两端插入，只允许一端弹出的也属于双端队列）。这个人的插队行为类似于下面这幅图。

 

 

 

 

 

 

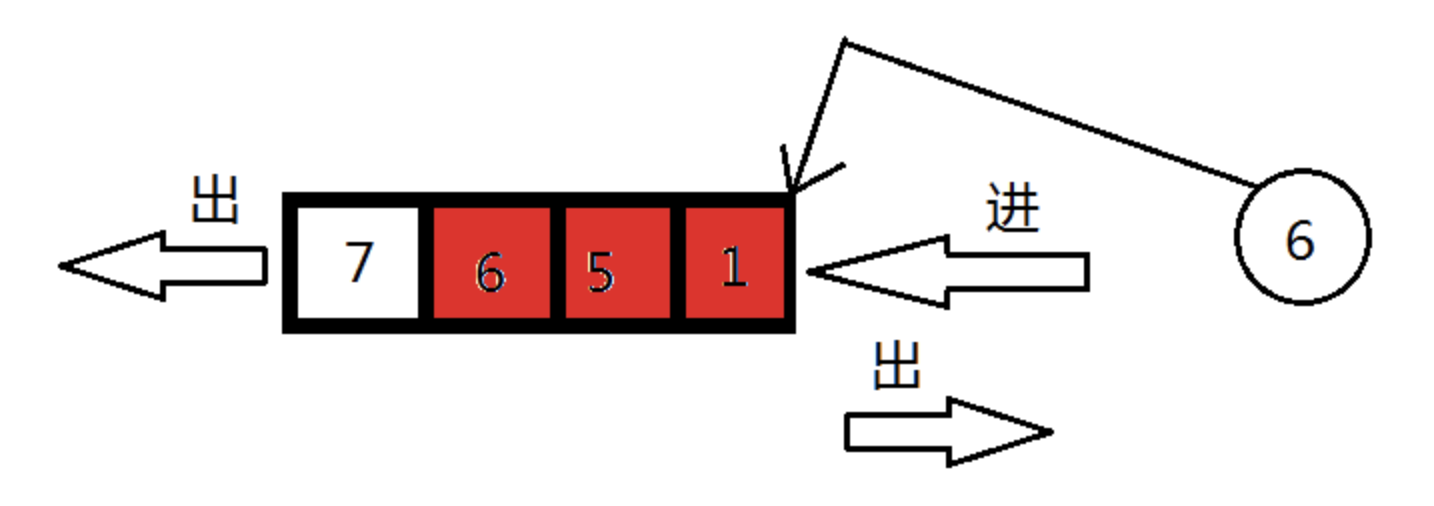
模板题：滑动窗口

题目一：求窗口内最大值和最小值

有一个长为 n 的序列 a，以及一个大小为 k 的窗口。现在这个从左边开始向右滑动，每次滑动一个单位，求出每次滑动后窗口中的最大值和最小值。

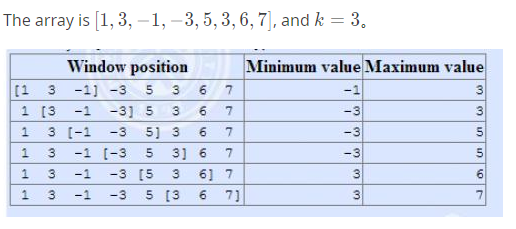
例如：

解析

求最大值

解法1：

　　如果按照常规方法，我们在求f[i]即i~i+m-1区间内的最值时，要把区间内的所有数都访问一遍，时间复杂度约为O（nm）。有没有一个快一点的算法呢？

解法2：

　　我们知道，上一种算法有一个地方是重复比较了，就是在找当前的f(i)的时候，i的前面k-1个数其它在算f(i-1)的时候我们就比较过了。那么我们能不能保存上一次的结果呢？当然主要是i的前k-1个数中的最大值了。答案是可以，这就要用到单调递减队列。

使用单调队列就涉及到去头和删尾：

1、队列的头一定是在一段时间前就加入了队列，现在的队列头会不会离开了我们处理的区间呢？如果它离我们正在处理的i太远了，我们就要把它去掉，去除冗杂的信息。

2、为了保证队列的递减性，在从列队尾新插入元素v时，要考虑队列尾的值是否大于v，如果是，队列呈现 队列尾-1的值 > 队列尾的值 > v ，此时队列递减性没有消失；如果不是，队列呈现 队列尾-1的值 > 队列尾的值 < v ，队列递减性被打破。

为了维护递减性，我们做如下考虑：v是最新值，它的位置是目前最靠后的，它可成为以后的最大值，必须留下；队列尾-1的值与v大小不定，不能冒然删去它；队列尾的值夹在v和队列尾-1之间，它不但不是最大值，对于以后的情况又不如v优，因为v相比队列尾更靠后（v可以影响到后m个值，队列尾只能影响到从它的位置往后数m-1个值），而且值更大，所以删队列尾是必定的。

 

核心代码如下：

c++

class Solution {
public:
    vector<int> maxSlidingWindow(vector<int>& nums, int k) {
        int n = nums.size();
        deque<int> q;
        for (int i = 0; i < k; ++i) {
            while (!q.empty() && nums[i] >= nums[q.back()]) {
                q.pop_back();
            }
            q.push_back(i);
        }

        vector<int> ans = {nums[q.front()]};
        for (int i = k; i < n; ++i) {
            while (!q.empty() && nums[i] >= nums[q.back()]) {
                q.pop_back();
            }
            q.push_back(i);
            while (q.front() <= i - k) {
                q.pop_front();
            }
            ans.push_back(nums[q.front()]);
        }
        return ans;
    }
};

java

class Solution {
    public int[] maxSlidingWindow(int[] nums, int k) {
        int n = nums.length;
        Deque<Integer> deque = new LinkedList<Integer>();
        for (int i = 0; i < k; ++i) {
            while (!deque.isEmpty() && nums[i] >= nums[deque.peekLast()]) {
                deque.pollLast();
            }
            deque.offerLast(i);
        }

        int[] ans = new int[n - k + 1];
        ans[0] = nums[deque.peekFirst()];
        for (int i = k; i < n; ++i) {
            while (!deque.isEmpty() && nums[i] >= nums[deque.peekLast()]) {
                deque.pollLast();
            }
            deque.offerLast(i);
            while (deque.peekFirst() <= i - k) {
                deque.pollFirst();
            }
            ans[i - k + 1] = nums[deque.peekFirst()];
        }
        return ans;
    }
}

python3

class Solution:
    def maxSlidingWindow(self, nums: List[int], k: int) -> List[int]:
        n = len(nums)
        q = collections.deque()
        for i in range(k):
            while q and nums[i] >= nums[q[-1]]:
                q.pop()
            q.append(i)

        ans = [nums[q[0]]]
        for i in range(k, n):
            while q and nums[i] >= nums[q[-1]]:
                q.pop()
            q.append(i)
            while q[0] <= i - k:
                q.popleft()
            ans.append(nums[q[0]])
        
        return ans

 

补充一个c++ 版本的数组实现版本求最小值

#include <algorithm>
#include <iostream>
#include <cstring>
#include <string>
#include <cstdio>
#include <cmath>
using namespace std;
const int N=1e6+500;
int n,k,a[N],q[N],head=1,tail;//head要+1 
int main()
{
    scanf("%d %d",&n,&k);
    for(int i=1;i<=n;i++)
    {
        //求最小值 
        scanf("%d",&a[i]);
        while(head<=tail&&q[head]<=i-k) head++;//队头显然是最早进入的,如果队头的下标大于i-k,该数便不在区间内了,从队头删除 
        while(head<=tail&&a[q[tail]]>=a[i]) tail--;//当前数破坏了单调性,从队尾删除,直至队中数小于当前数
        q[++tail]=i;//当前元素进队 
        if(i>=k) printf("%d ",a[q[head]]);//输出每个区间最小值 
    }
    printf("\n");
    head=1,tail=0;
    for(int i=1;i<=n;i++)
    {    //求最大值 
        while(head<=tail&&q[head]<=i-k) head++;
        while(head<=tail&&a[q[tail]]<=a[i]) tail--;
        q[++tail]=i;//当前元素进队 
        if(i>=k) printf("%d ",a[q[head]]);
    }
    return 0;
}

具体实现时，我们令head表示队列头+1,tail表示队列尾，

那么问题来了，为什么head要+1呢？

试想一下，如果head不+1,那么当head=tail时，队列中到底是没有数还是有1个数呢？显然无法判断。

所以我们令head的值+1，当head<=tail时，队列中便是有值的,如果head>tail，队列便为空。

我们用样例来模拟一下单调队列，以求最小值为例：

• i=1，队列为空，1进队，[1]
• i=2，3比1大，满足单调性，3进队，[1,3]
• i=3，-1比3小，破坏单调性，3出队，-1比1小，1出队，队列为空，-1进队[-1]，此时i>=k，输出队头，即-1
• i=4，-3比-1小，-1出队，队列为空，-3进队[-3]，输出-3
• i=5，5比-3大，5进队，[-3,5]，输出-3
• i=6，3比5小，5出队，3比-3大，3进队，[-3,3]，输出-3
• i=7，-3下标为4，i-4=3，大于等于k，-3已不在区间中，-3出队，6比3大，6进队，[3,6]，输出3
• i=8，7比6大，7进队，[3,6,7]，输出3

这样最小值便求完了，最大值同理，只需在判断时改变符号即可。

 

解法3：

　　当然，这题也可以用优先队列做。其中的大根堆可以帮助我们实时维护一系列元素中的最大值。

对于本题而言，初始时，我们将数组 nums 的前 k 个元素放入优先队列中。每当我们向右移动窗口时，我们就可以把一个新的元素放入优先队列中，此时堆顶的元素就是堆中所有元素的最大值。然而这个最大值可能并不在滑动窗口中，在这种情况下，这个值在数组 nums 中的位置出现在滑动窗口左边界的左侧。因此，当我们后续继续向右移动窗口时，这个值就永远不可能出现在滑动窗口中了，我们可以将其永久地从优先队列中移除。

我们不断地移除堆顶的元素，直到其确实出现在滑动窗口中。此时，堆顶元素就是滑动窗口中的最大值。为了方便判断堆顶元素与滑动窗口的位置关系，我们可以在优先队列中存储二元组 (num,index)，表示元素 num 在数组中的下标为 index。

java

class Solution {
    public int[] maxSlidingWindow(int[] nums, int k) {
        int n = nums.length;
        PriorityQueue<int[]> pq = new PriorityQueue<int[]>(new Comparator<int[]>() {
            public int compare(int[] pair1, int[] pair2) {
                return pair1[0] != pair2[0] ? pair2[0] - pair1[0] : pair2[1] - pair1[1];
            }
        });
        for (int i = 0; i < k; ++i) {
            pq.offer(new int[]{nums[i], i});
        }
        int[] ans = new int[n - k + 1];
        ans[0] = pq.peek()[0];
        for (int i = k; i < n; ++i) {
            pq.offer(new int[]{nums[i], i});
            while (pq.peek()[1] <= i - k) {
                pq.poll();
            }
            ans[i - k + 1] = pq.peek()[0];
        }
        return ans;
    }
}

c++

class Solution {
public:
    vector<int> maxSlidingWindow(vector<int>& nums, int k) {
        int n = nums.size();
        priority_queue<pair<int, int>> q;
        for (int i = 0; i < k; ++i) {
            q.emplace(nums[i], i);
        }
        vector<int> ans = {q.top().first};
        for (int i = k; i < n; ++i) {
            q.emplace(nums[i], i);
            while (q.top().second <= i - k) {
                q.pop();
            }
            ans.push_back(q.top().first);
        }
        return ans;
    }
};

python

class Solution:
    def maxSlidingWindow(self, nums: List[int], k: int) -> List[int]:
        n = len(nums)
        # 注意 Python 默认的优先队列是小根堆
        q = [(-nums[i], i) for i in range(k)]
        heapq.heapify(q)

        ans = [-q[0][0]]
        for i in range(k, n):
            heapq.heappush(q, (-nums[i], i))
            while q[0][1] <= i - k:
                heapq.heappop(q)
            ans.append(-q[0][0])
        
        return ans

 

 

题目二

烽火台又称烽燧，是重要的军事防御设施，一般建在险要或交通要道上。一旦有敌情发生，白天燃烧柴草，通过浓烟表达信息；夜晚燃烧干柴，以火光传递军情，在某两座城市之间有 n 个烽火台，每个烽火台发出信号都有一定代价。为了使情报准确地传递，在连续 m 个烽火台中至少要有一个发出信号。请计算总共最少花费多少代价，才能使敌军来袭之时，情报能在这两座城市之间准确传递。

Input

　　第一行：两个整数 N，M。其中N表示烽火台的个数， M 表示在连续 m 个烽火台中至少要有一个发出信号。接下来 N 行，每行一个数 Wi，表示第i个烽火台发出信号所需代价。

Output

　　一行，表示答案。

Sample Input

5 3
1
2
5
6
2

Sample Output

4

Data Constraint

对于50%的数据，M≤N≤1,000 。 对于100%的数据，M≤N≤100,000，Wi≤100。

分析题目，由于题目要求连续m个烽火台中至少要有一个发出信号，很容易得出DP转移方程：

F[i]=min(F[j]:i−m<j<i)+a[i]

最直接的方法是枚举状态，对于每一个i，我们在i-m+1到i-1中寻找一个最小的F[j]进行状态转移，枚举状态的时间复杂度是O(n)，寻找最小值的状态时间复杂度是O(n)，因此这种方法的复杂度是O(n^2)。题目的是数据范围是n<=100000，显然超时。
那么怎么用单调队列优化呢？

如图：

 

 

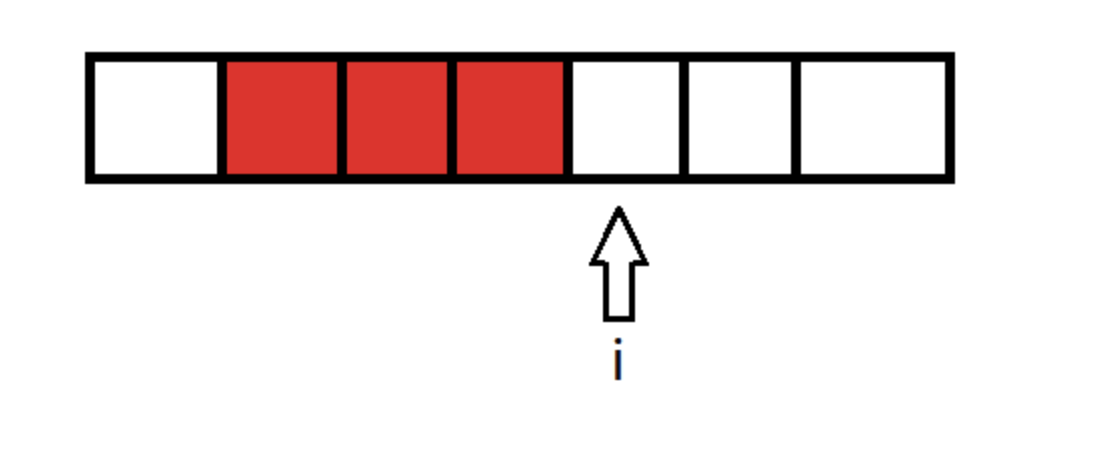
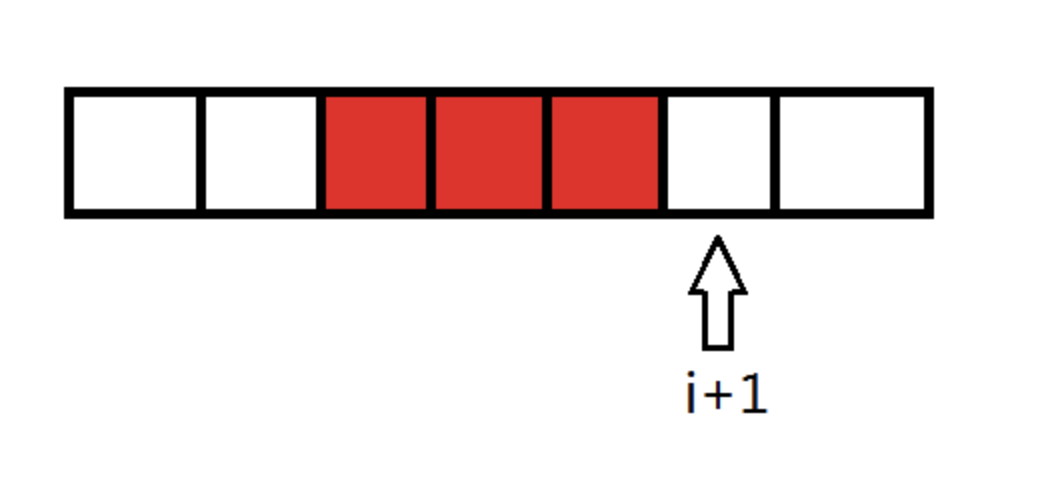
上图中，状态枚举到i，当m=4时，我们要做的就是在i-3到i-1中找到最小的F[j]，那么枚举到i+1时，我们要做的就是要在i-2到i中找到最小的F[j]。

上图中我们可以看出，要寻找最小值的区间向后移动了一位，也就是F[i-m+1]的值被抛弃，F[i-1]的值被加入。这里就可以用单调队列处理了，F[i-1]是插队的数据，F[i-1]有资格插队是因为它更优且更靠近i，比它更差的数将被它取代，保留那些数据没有任何好处。而那些已经不再维护区间之外的就不必再对其进行维护，出队即可。看了代码会更加明白：

Python3

class Solution:
    def getMinPrice(self, n, m, price):
        head = 1
        tail = 0
        ans = float("inf")
        price = [0] + price
        que = [0] * (n + 1)
        f = [0] * (n + 1)
        for i in range(1, n + 1):
            # 当F[i-1]比队尾值更优时把队尾值弹出
            while head <= tail and f[i - 1] <= f[que[tail]]:
                tail -= 1
            # 把F[i-1]插入，这里插入下标而不插入值，便于从队头弹出
            tail += 1
            que[tail] = i - 1
            # 不属于区间维护内的数弹出
            while head <= tail and que[head] < i - m:
                head += 1
            f[i] = f[que[head]] + price[i]

        for i in range(n, n - m, -1):
            ans = min(ans, f[i])
        print(ans)


if __name__ == '__main__':
    n, m = 5, 3
    price = [1, 2, 5, 6, 2]
    s = Solution()
    s.getMinPrice(n, m, price)

 

 

题目三：切蛋糕

题目

今天是小Z的生日，同学们为他带来了一块蛋糕。这块蛋糕是一个长方体，被用不同色彩分成了N个相同的小块，每小块都有对应的幸运值。

小Z作为寿星，自然希望吃到的第一块蛋糕的幸运值总和最大，但小Z最多又只能吃M小块(M≤N)的蛋糕。

吃东西自然就不想思考了，于是小Z把这个任务扔给了学OI的你，请你帮他从这N小块中找出连续的k块蛋糕(k≤M)，使得其上的幸运值最大。

【输入格式】

输入文件cake.in的第一行是两个整数N,M。分别代表共有N小块蛋糕，小Z最多只能吃M小块。

第二行用空格隔开的N个整数，第i个整数Pi代表第i小块蛋糕的幸运值。

【输出格式】

输出文件cake.out只有一行，一个整数，为小Z能够得到的最大幸运值。

【输入样例】

6 3
1 -2 3 -4 5 -6

【输出样例】

5 

【数据规模】

对20%的数据，N≤100。

对100%的数据，N≤500000，|Pi|≤500。 答案保证在2^31-1之内。

解析

因为蛋糕是连续的，所以不难联想到前缀和，令sum[i]表示从第1块到第i块蛋糕的幸运值之和。

于是很自然的想到了暴力：从1到n枚举i，从i-M+1到i枚举j，那么最大幸运值maxn=max(maxn,sum[i]-sum[j-1])

但是这样显然会超时，考虑优化。

对于每一个i来说，实际上我们只需要找到最小的sum[j-1]即可，所以我们可以用单调递增队列来维护最小的sum[j-1]的值，

那么这不就是一个滑动窗口么？数列为sum[1]~sum[n]，区间长度为1~M，求每个区间的最小值，

唯一不同的就是区间长度不是一个定值，而是1~M，但这也不难办，依旧只需保证队列长度不超过M即可。

 

Python代码

class Solution:
    def getMaxLucky(self, n, m, lucky):
        head, tail = 1, 0
        lucky = [0] + lucky
        sums = [0] * (n + 1)
        q = [0] * (n + 1)

        max_ = float("-inf")

        for i in range(1, n + 1):
            sums[i] = sums[i - 1] + lucky[i]
        for i in range(1, n + 1):
            while head <= tail and i - q[head] > m:
                head += 1
            max_ = max(max_, sums[i] - sums[q[head]])
            while head <= tail and sums[q[tail]] >= sums[i]:
                tail -= 1
            tail += 1
            q[tail] = i

        return max_


if __name__ == '__main__':
    n, m, = 6, 3
    lucky = [1, -2, 3, -4, 5, -6]
    s = Solution()
    print(s.getMaxLucky(n, m, lucky))