set

\(update2022.9.20\) 更新一个代码以便加深记忆

用处

\(set\)更多的用在可以用平衡树做的题目中，换句话说，平衡树的题用\(set\)一般都可以做。\(set\)支持查找一序列的长度、是否为空，可以随时插入、删除元素，可以查找某个点的前驱后继等。

用法

调用

\(set\)作为\(STL\)，要用到专门的头文件。

#include<set>

\(set\)的调用与\(queue\)等类似：\(set<\)类型\(>\) 名称，如：

set<int> a;

注意，\(set\)中的元素不可重复，若有重复，应用\(multiset\)。

常用操作（以名称为\(a\)的\(set\)为例）

1. 插入：\(a.insert(x)\)，向\(a\)中插入一个元素\(x\)。
2. 删除：\(a.erase(x)\)，把\(a\)中所有值为\(x\)的元素全部删除。
3. 查找：\(a.find(x)\)，查找\(a\)中第一个值为\(x\)的元素的地址。
4. 是否为空：\(a.empty()\)，判断是否为空，用法与\(queue\)一样。
5. 大小：\(a.size()\)，返回\(a\)的大小，即元素个数。
6. 前驱：\(a.upper\)_\(bound(x)\)，返回第一个大于\(x\)的元素的地址。
7. 后继：\(a.lower\)_\(bound(x)\)，不是真正意义上的后继，是返回第一个大于等于\(x\)的元素的地址，要想求后继要将地址\(-1\)。
8. 第一个值：\(a.rbegin()\)，返回\(a\)中的第一个值，即最大值。
9. 末一个值：\(a.end()\)，返回\(a\)中的最后一个值，即最小值。

10
1 4 5 5 6 6 7 8 8 9
Now put them in a multiset 'a'

The result of *a.find(5) is 5
The result of *a.upper_bound(5) is 6
The result of *a.upper_bound(7) is 8
The result of *a.lower_bound(5) is 5
The result of *(a.lower_bound(5)--) is 4
The result of *a.lower_bound(7) is 7
The result of *(a.lower_bound(7)--) is 6
The result of *a.rbegin() is 9
The result of *a.end() is 10

Now a.erase(4) and a.erase(6)
Now...
The result of a.size() is 7
The result of *a.upper_bound(5) is 7
The result of *a.upper_bound(7) is 8
The result of *a.lower_bound(5) is 5
The result of *(a.lower_bound(5)--) is 1
The result of *a.lower_bound(7) is 7
The result of *(a.lower_bound(7)--) is 5

Now a.erase(a.find(8))
Now...
The result of a.size() is 6

例题：CF528A Glass Carving

题意

有一块长\(n\)宽\(m\)的玻璃，现进行若干次横向（\('H'\)）或纵向（\('V'\)）的切割，问每次切割后的得到的最大玻璃是多少。

思路

显然，切割后剩下的玻璃中，最大的那块一定是横向最长边与纵向最长边构成的，如图：

那么，我们只要在每次操作后计算横向及纵向的最大值的积即可。
注意到我们使用的数据结构应支持删除（删去被切割的边）、插入（添加新得到的两条边）、找最值（横向及纵向的最大长度）、找前驱后继（确定切割点所在边的长度及得到的边的长度）操作，很容易就能想到\(set\)。具体解释如下：

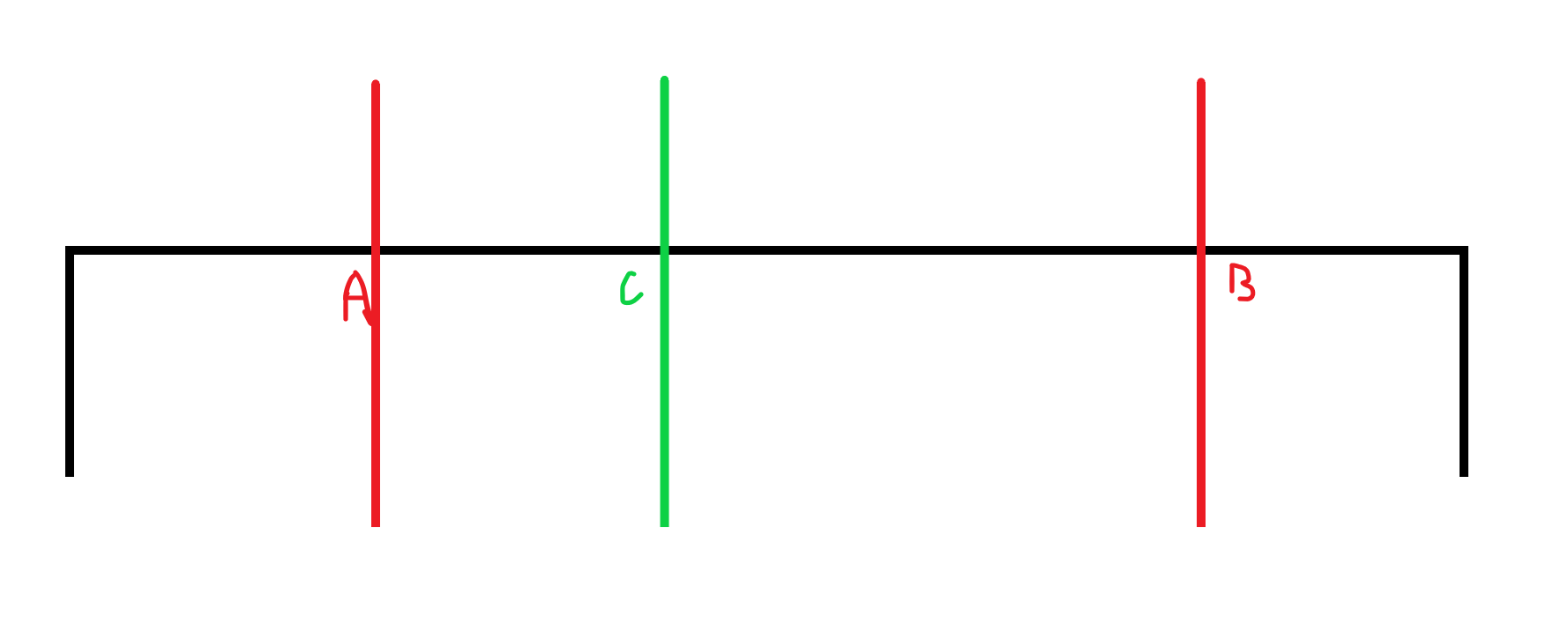
如图，红色为已切割处，当要在绿色部分切割时：对于点来说，只是新增了一个点\(C\)，而对于边来说，我们要先找到点\(C\)的前驱\(A\)和后继\(B\)，然后在边中减去一条长为\(AB\)的边，因为它被切割了，而插入两条长为\(AC\)和\(CB\)的边。根据这些，我们可以得出代码。

代码

#include<iostream>
#include<cstdio>
#include<set> 
using namespace std;
int n,m,q,x;//'V'->n  'H'->m
char opt;
set<int> point1,point2;
multiset<int> edge1,edge2;
int main(){
	scanf("%d%d%d",&n,&m,&q);
	point1.insert(0);
	point1.insert(n);
	edge1.insert(n);
	point2.insert(0);
	point2.insert(m);
	edge2.insert(m);
	while(q--){
		scanf("\n%c%d",&opt,&x);
		if(opt=='V'){
			set<int>::iterator pre=point1.upper_bound(x),nex=point1.lower_bound(x);
			nex--;
			edge1.insert(x-*nex);
			edge1.insert(*pre-x);
			edge1.erase(edge1.find(*pre-*nex)); 
			point1.insert(x);
		}else if(opt=='H'){
			set<int>::iterator pre=point2.upper_bound(x),nex=point2.lower_bound(x);
			nex--;
			edge2.insert(x-*nex);
			edge2.insert(*pre-x);
			edge2.erase(edge2.find(*pre-*nex));
			point2.insert(x);	
		}
		printf("%lld\n",(long long)(*edge1.rbegin())*(*edge2.rbegin()));
	}
	return 0;
}