平衡树学习笔记

平衡树

算法简介

平衡树是一种支持

  1. 插入一个整数 \(\text{x}\)。

  2. 删除一个整数 \(\text{x}\)（若有多个相同的数，只删除一个）。

  3. 查询整数 \(\text{x}\) 的排名（排名定义为比当前数小的数的个数 \(\text{+1}\)）。

  4. 查询排名为 \(\text{x}\) 的数（如果不存在，则认为是排名小于 \(\text{x}\) 的最大数）。

  5. 求 \(\text{x}\) 的前驱（前驱定义为小于 \(\text{x}\)，且最大的数）。

  6. 求 \(\text{x}\) 的后继（后继定义为大于 \(\text{x}\)，且最小的数）。

等操作，并且支持在线的数据结构

分类

  1. 伪平衡树（并不是平衡树）
  2. Treap
  3. 替罪羊树
  4. AVL树
  5. 伸展树
  6. 红黑树

这里讲前两种

伪平衡树

注意：这并不是平衡树，只是可以支持大部分平衡树的操作的一种结构

实质：\(\text{stl}\) (\(\text{vector}\) + \(\text{lower_bound}\))

vector

\(\text{vector}\) 是一种支持任意位置插入、删除和查询的一个结构。

定义方法std::vector<int>vec;//其中int可改为任意结构

它有以下几个常用函数：

  1. push_back(x)在尾部加入一个元素 x
  2. insert(pos,x) 在 pos 位置插入一个元素 x
  3. pop_back()在尾部删除一个元素
  4. erase(pos)在 pos 位置删除一个元素
  5. begin()返回第一个元素的位置
  6. end()返回最后一个元素的位置
  7. "operator[x]" 返回第 x 个元素

lower_bound

\(\text{lower_bound}\) 是 \(\text{stl}\) 自带的二分查找函数。

用法：std::lower_bound(/*起始地址*/,/*结束地址*/,/*所查询元素*/)

它会返回第一个小于等于所查询元素的位置。

实现

#include<bits/stdc++.h>
using namespace std;
int N,opt,x;
vector<int>vec;
int main() {
    scanf("%d",&N);
    while(N--) {
        scanf("%d%d",&opt,&x);
        if(opt==1) {vec.insert(lower_bound(vec.begin(),vec.end(),x),x);}
        if(opt==2) {vec.erase(lower_bound(vec.begin(),vec.end(),x));}
        if(opt==3) {printf("%d\n",lower_bound(vec.begin(),vec.end(),x)-vec.begin()+1);}
        if(opt==4) {printf("%d\n",vec[x-1]);}
        if(opt==5) {printf("%d\n",*(lower_bound(vec.begin(),vec.end(),x)-1));}
        if(opt==6) {printf("%d\n",*lower_bound(vec.begin(),vec.end(),x+1));}
    }
}

优缺点

优点：代码简短，不易打挂，易调试，支持在线。

缺点：由于 \(\text{vector}\) 和 \(\text{lower_bound}\) 的嵌套使用，时间复杂度较高。

适用于：

  1. 数据范围较小（一般 \(\text{n}\le10^6\) 均可）

  2. 对常数要求不高的平衡树算法

Treap

Treap这个名字十分有内涵：

\[\color{red}{Tree} \color{black}{+} \color{blue}{Heap} \color{black}{=} \color{red}{Tre} \color{black}{+} \color{blue}{eap} \color{black}{=} \color{red}{Tr}\color{purple}{e}\color{blue}{ap} \]

即 \(\text{Treap}\) = \(\text{Tree}\)(二叉搜索树) + \(\text{Heap}\)(堆)

这也是 \(\text{Treap}\) 能够平衡的关键。

基础操作

节点

对于每一个节点我们都会给它以下几个参数：

struct Treap{
    int l,//左儿子
    	r,//右儿子
    	val,//键值
    	ord,//随机值
    	siz,//子树大小
    	num;//同键值的数的个数
}t[Maxn];

旋转

旋转分为左旋（\(\text{zig}\)）和右旋（\(\text{zag}\)），如下图：

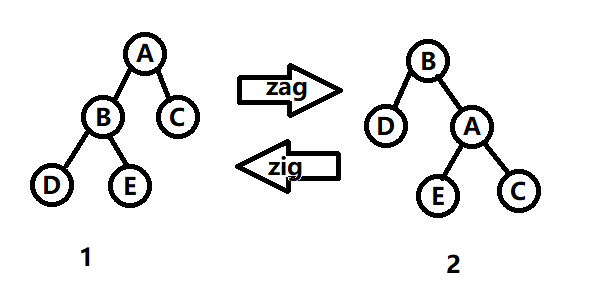
zig-zag

图1的中序遍历：\(D\to B\to E\to A\to C\)

图2的中序遍历：\(D\to B\to E\to A\to C\)

可以发现 \(\text{zig}\) 和 \(\text{zag}\) 是不改变树的中序遍历的

所以我们就可以在原树上放心的使用 \(\text{zig}\) 和 \(\text{zag}\) 来让树平衡

void zag(int &u){
    int tmp=t[u].l;
    t[u].l=t[tmp].r;
	t[tmp].r=u,u=tmp;
    pushup(t[u].r);pushup(u);
}

void zig(int &u){
    int tmp=t[u].r;
    t[u].r=t[tmp].l;
	t[tmp].l=u,u=tmp;
    pushup(t[u].l);pushup(u);
}

插入

插入操作与 \(\text{BST}\) 基本相同，对于一个已经拥有的节点，直接 \(\text{num} + 1\to\text{num}\)即可。

对于一个新节点，我们先给他一个随机的 \(\text{ord}\) 值，按照 \(\text{BST}\) 的方法插入

回溯时判断是否进行旋转。

void insert(int &u,int x){
    if(!u){sz++,u=sz;t[u].siz=t[u].num=1;t[u].val=x,t[u].ord=rand();return;}
    if(t[u].val==x){t[u].num++;t[u].siz++;}
    else if(t[u].val<x){insert(t[u].r,x);if(t[t[u].r].ord<t[u].ord)zig(u);}
    else if(t[u].val>x){insert(t[u].l,x);if(t[t[u].l].ord<t[u].ord)zag(u);}
    pushup(u);
}

删除

删除和 \(\text{BST}\) 也是基本相同，对于 \(2\leq\text{num}\) ，\(\text{num} - 1\to\text{num}\)。

否则将此节点移动到叶子，然后删除其与父节点的连边。

void del(int &u, int x){
    if(t[u].val==x){
        if(t[u].num>1){t[u].num--,t[u].siz--;}
        else if(!t[u].l){u=t[u].r;}
        else if(!t[u].r){u=t[u].l;}
        else if(t[t[u].l].ord<t[t[u].r].ord){zag(u);del(t[u].r,x);}
        else if(t[t[u].l].ord>t[t[u].r].ord){zig(u);del(t[u].l,x);}
    }
    else if(t[u].val>x){del(t[u].l,x);}
    else if(t[u].val<x){del(t[u].r,x);}
    pushup(u);
}

查询排名与元素

这两个都和 \(\text{BST}\) 完全一样。

查询元素的排名
int queryrnk(int u, int x){
    if(!u)return 1;
    else if(t[u].val==x) return t[t[u].l].siz+1;
    else if(x>t[u].val) return t[t[u].l].siz+t[u].num+queryrnk(t[u].r,x);
    else if(x<t[u].val) return queryrnk(t[u].l,x);
}
查询排名的元素
int querynum(int u, int x){
    if(x<=t[t[u].l].siz+t[u].num&&x>t[t[u].l].siz)return t[u].val;
    else if(x<=t[t[u].l].siz)return querynum(t[u].l,x);
    else return querynum(t[u].r,x-t[t[u].l].siz-t[u].num);
}

前驱和后继

int querypre(int u, int x){
    if(!u){return -(0x3fffffff);}
    if(t[u].val<x)return max(t[u].val,querypre(t[u].r,x));
    else return querypre(t[u].l,x);
}
int querysub(int u, int x){
    if(!u){return +(0x3fffffff);}
    if(t[u].val>x)return min(t[u].val,querysub(t[u].l,x));
    else return querysub(t[u].r,x);
}

实现

#include<bits/stdc++.h>
using namespace std;
#define Maxn 1000039
struct Treap {int l,r,val,ord,siz,num;} t[Maxn];
int N,op,x,sz=0,rt=1,tmp;
void pushup(int u) {t[u].siz=t[t[u].l].siz+t[t[u].r].siz+t[u].num;}
void zig(int &u) {tmp=t[u].r;t[u].r=t[tmp].l;t[tmp].l=u,u=tmp;pushup(t[u].l);pushup(u);}
void zag(int &u) {tmp=t[u].l;t[u].l=t[tmp].r;t[tmp].r=u,u=tmp;pushup(t[u].r);pushup(u);}
void insert(int &u,int x) {
	if(!u) {sz++,u=sz;t[u].siz=t[u].num=1;t[u].val=x,t[u].ord=rand();return;}
	if(t[u].val==x) {t[u].num++;t[u].siz++;} 
	else if(t[u].val<x) {insert(t[u].r,x);if(t[t[u].r].ord<t[u].ord)zig(u);} 
	else if(t[u].val>x) {insert(t[u].l,x);if(t[t[u].l].ord<t[u].ord)zag(u);}
	pushup(u);
}
void del(int &u, int x) {
	if(t[u].val==x) {
		if(t[u].num>1) {t[u].num--,t[u].siz--;} 
		else if(!t[u].l) {u=t[u].r;} 
		else if(!t[u].r) {u=t[u].l;} 
		else if(t[t[u].l].ord<t[t[u].r].ord) {zag(u);del(t[u].r,x);} 
		else if(t[t[u].l].ord>t[t[u].r].ord) {zig(u);del(t[u].l,x);}
	} 
	else if(t[u].val>x) {del(t[u].l,x);} 
	else if(t[u].val<x) {del(t[u].r,x);}
	pushup(u);
}
int queryrnk(int u, int x) {
	if(!u)return 1;
	else if(t[u].val==x) return t[t[u].l].siz+1;
	else if(x>t[u].val) return t[t[u].l].siz+t[u].num+queryrnk(t[u].r,x);
	else if(x<t[u].val) return queryrnk(t[u].l,x);
}
int querynum(int u, int x) {
	if(x<=t[t[u].l].siz+t[u].num&&x>t[t[u].l].siz)return t[u].val;
	else if(x<=t[t[u].l].siz)return querynum(t[u].l,x);
	else return querynum(t[u].r,x-t[t[u].l].siz-t[u].num);
}
int querypre(int u, int x) {
	if(!u) {return -(0x3fffffff);}
	if(t[u].val<x)return max(t[u].val,querypre(t[u].r,x));
	else return querypre(t[u].l,x);
}
int querysub(int u, int x) {
	if(!u) {return +(0x3fffffff);}
	if(t[u].val>x)return min(t[u].val,querysub(t[u].l,x));
	else return querysub(t[u].r,x);
}
void init() {
	srand(time(0));
	sz++;t[sz].siz=t[sz].num=1;
	t[sz].val=-(0x3fffffff),t[sz].ord=rand();
	sz++;t[sz].siz=t[sz].num=1;
	t[sz].val=+(0x3fffffff),t[sz].ord=rand();
	t[1].r=2;pushup(1);
}
int main() {
	init();
	scanf("%d",&N);
	while(N--) {
		scanf("%d%d",&op,&x);
		if(op==1) {insert(rt,x);}
		if(op==2) {del(rt,x);}
		if(op==3) {printf("%d\n",queryrnk(rt,x)-1);}
		if(op==4) {printf("%d\n",querynum(rt,x+1));}
		if(op==5) {printf("%d\n",querypre(rt,x));}
		if(op==6) {printf("%d\n",querysub(rt,x));}
	}
	return 0;
}

优缺点

优点：代码与 \(\text{BST}\) 差距不大，简单易调试，支持在线，速度快。

缺点：由于关键字是随机的，不一定是稳定的\(\log{\text{n}}\)

适用于：

  1. 无法使用 \(\text{vector}\)+\(\text{lower_bound}\) 的其他大部分的题基本都可以
posted @ 2022-09-14 17:58  qzccy  阅读(128)  评论(0)    收藏  举报