2025.10 做题记录
专题
SA
link。
散题
校内模拟赛 删数(delete)
solution
注意到后面的数删掉是对前面的数没有任何影响的,但是前面的数删掉可能会让后面的某些数符合条件。
也就是说,一个位置 \(i\) 只要满足前面可以删的位置大于等于 \(i-a_i\),这个数就一定可以贡献进答案。
于是考虑对于 \(r\) 扫描线,同时维护对于每个 \(l\) 的答案 \(ans_l\)。每次添加一个 \(r\) 时,由上面的结论,\(\forall ans_l\ge r-a_r\),\(ans_l+1\)。同时显然 \(ans_l\) 单调不降,所以被更新的答案一定是一段前缀。
可以使用线段树上二分找到满足 \(ans_l\ge r-a_r\) 的最大 \(l\) 并更新 \([1,l]\)。复杂度 \(O(n\log n)\)。
注意当 \(a_r>r\) 时这个位置不可能被删掉,所以不能更新。
校内模拟赛 账本(book)
很妙。
description

solution
把 + 视为 \(1\),- 视为\(-1\)。\(s_i\) 表示到第 \(i\) 位的前缀和。
先考虑没有右移操作怎么做。因为第二个条件满足后再做第一个条件可能破坏答案,所以先尝试满足第一个条件。
相当于把一些 \(-1\) 改成 \(1\),最后需要 \(\forall s_i\ge 0\)。观察到如果这样操作使得 \(\min s_i\ge 0\),一定可以通过最优操作使得 \(\forall s_i\ge 0\)(即操作最前的一些 \(-1\))。所以只要找到了 \(\min s_i\),答案就可以 \(O(1)\) 求出。
现在加上第二个操作。我们可以把原数组复制两遍,枚举起点(得到右移操作的耗时),计算长度为 \(n\) 的段的答案。扫描线的时候维护区间最小值可以单调队列套路地做。
复杂度 \(O(n)\)。
CF2138C2 Maple and Tree Beauty (Hard Version)
solution1
设 \(a_i\) 为深度为 \(i\) 的点的个数。
我们断言题目中的“公共子序列”取公共前缀一定不劣。感性理解即可。
题目转化为你有一些体积 \(v_i=a_i\),价值 \(w_i=1\) 的物品和两个容量分别为 \(k,n-k\) 的背包,问总价值最大是多少。
因为最优解一定是取一段前缀,所以可以设状态 \(dp_{i,j}\) 为取了前 \(i\) 个物品,第一个背包用了 \(j\) 的容量(第二个背包用的容量为 \((\sum w-j)\))是否可行。转移有:
\(dp_{i,j}\gets dp_{i-1,j} \vee dp_{i-1,j-w_i}\),注意需要满足 \(n-k-(\sum w-j)\ge 0\)。
转移可以使用 bitset 优化。满足条件的 \(j\) 随着 \(i\) 的增加而单调不降,所以可以维护一个符合条件的 \(j\) 的 bitset \(G\),每次 \(i\) 增加时暴力推平一段即可。
复杂度 \(O(\dfrac{n^2}{w})\),时限 6s,应该可以过。
solution2
还可以优化。
考虑根号分治。因为 \(\sum a=n\),所以 \(v_i>\sqrt n\) 的 \(i\) 不超过 \(\sqrt n\) 个。而个数超过 \(\sqrt n\) 的 \(v\) 不超过 \(\sqrt n\) 种。
对于 \(v_i> \sqrt n\) 的我们仍然按照上文暴力处理。
对于个数超过 \(\sqrt n\) 的,问题转化为有 \(\sqrt n\) 种物品,每种物品不超过 \(\sqrt n\) 个的多重背包。
我们使用二进制拆分优化。hsz 证明这里二进制分组分出来的物品数量是 \(O(\sqrt n)\) 的。我不会。
但是有一个现有的二进制分组优化的题解(其实很少)没有提到过的问题:把一个物品拆成 \(\log n\) 种不同的物品后,由于 \(w_i\) 不再满足全都是 \(1\),所以并不能保证取一段前缀物品是最优的。
举个例子,如果有一个物品的体积为 \(1\),个数为 \(7\),拆成了体积和价值分别为 \(1,2,4\) 的物品。 此时背包剩余容量为 \(4\),但是按照原做法我们只能取到前两个物品,显然不优。
观察发现,这种情况只有在原本同一种物品分出来的一堆物品无法全部取完的时候才可能出现(其他情况的跟暴力没有区别,正确性有保障)。
后面的处理就很自然了:每扫到一种物品,判断这种物品能不能全部取完(因为假设取完,所以这里还是用二进制拆分做)。如果可以就直接继续做;否则,枚举 \(j\),再把第一个背包剩余的容量和第二个背包剩余的容量分别全部塞满当前物品,得到的最大价值就是答案。
还是判断可行性的 01 背包,所以依然可以 bitset 优化。最终做到复杂度 \(O(\dfrac{n \sqrt n}{w})\)。
code
不知道是不是实现太不精细导致常数爆炸,感觉跑出来效率跟暴力区别不大()。
Submission。尾数 0528 祭!
CF2127E Ancient Tree
可以记一下:看到需要一类点的 lca 可以想到虚树。
solution1
记 \(cnt_u\) 为最终 \(u\) 的多个子树中出现过的颜色 \(k\) 的种类数。一个节点是 cutie 就可以刻画成下面两种情况:
- \(cnt_u\ge 2\)
- \(cnt_u=1\land k\neq c_u\)
我们断言一个节点最后会是 cutie 当且仅当它在给出的染色方案中就是 cutie。
可以对于一开始没染色的节点给出构造:
- \(cnt_u=1\):染成唯一的那种颜色 \(k\)。
- 否则,\(u\) 是否 cutie 已经固定了。于是染成 \(u\) 子树内的任意一种颜色,使得祖先的 \(cnt\) 不会变大。
- 若 \(u\) 子树内本身没有颜色,那把它们全部染成 \(fa_u\) 的颜色,原理同上。
可以证明,这样操作的话不可能增加新的 cutie 节点。
现在需要求出每个节点的 \(cnt\)。
可以对于每个节点维护一个 set 表示它子树内的点。顺次合并 \(u\) 的子树时,每次暴力枚举哪些颜色在两个集合都出现了,最后启发式合并两个 set。复杂度 \(O(n\log^2 n)\)。
得到 \(cnt\) 后两次 dfs 可以简单完成上述染色方案构造。
solution2
注意到一个点是两个同色点的 lca 时,它一定在那种颜色的点建出来的虚树上。于是对于每种颜色建虚树,就可以得到 \(cnt\)。复杂度 \(O(n\log n)\),因为我不会线性建虚树。
code
校内模拟赛 投票(vote)
场上推一半躺下了。?根本就不难。
solution
第 \(i\) 个答案 \(ans_i=\sum_{j=p}^{n-i} \binom{n-i}{j}\),第 \(i+1\) 个答案 \(ans_{i+1}=\sum_{j=p'}^{n-i-1} \binom{n-i-1}{j}\)。
于是求出 \(2\sum_{j=p}^{n-i-1}\binom{n-i-1}{j}\) 是 \(O(1)\) 的,同时注意到 \(p'-p\le 1\),直接暴力更新即可。
复杂度 \(O(n)\)。
四校联考 灯泡(bulb)
彻底怒了吧,做了三个小时不会。
solution
首先对于每个 \(x\),它们出现次数的奇偶性不变,即所有 \(x\) 的异或和不变。
(赛时没想到这个啊)每条 \(x+y=k\) 的斜线同上。做完了。
P12652 [KOI 2024 Round 2] 拔树游戏
完全想不到。虽然合理但是对我来说并不自然。
solution
一个点可以在一轮操作中可以被提到根上,当且仅当它的父亲已经被提到根上过。于是就动态维护可以作为答案的点,每次找到权值最小的删掉并加入它的子节点即可。优先队列简单维护(类似 dijkstra)。
四校联考 金币(coin)
设 \(dp_{i,x,y}\) 为操作 \(i\) 轮后,金币在 \(x,y\) 的方案数。
实际上,有很多状态是本质相同的,最后只有三大类:
- \((s,t)\)
- \((s,i)\) 或 \((t,i)\)
- \((i,j)\)
\(i,j\neq s,t\)。
算出系数后矩乘转移即可。注意最后的答案是所有情况的和,所以每一类还需要除以情况数。
QOJ#1821 Ketek Counting
人类智慧题。
description
给定一个字符串 ,包含小写字母和 ?。 你可以把问号替换为任意小写字母(不必相同),然后把这个字符串划分成若干词 \(w_1,w_2,\cdots,w_k\),如果 \(w\) 是一个回文序列,那么这是一个好的句子。
求能操作出多少种好的句子,两个句子不同当且仅当构成其的词序列不一样。
solution
原来的条件太难刻画了,考虑把字符串换一个形式:把前一半字符依次放在奇数位置,后一半字符反着依次放在偶数位置。这样操作后的字符串形如(字符串从 \(1\) 开始编号):\(s_1,s_n,s_2,s_{n-1},\cdots\)。你惊奇的发现条件变成了,更改后的字符串可以划分成若干个长度为偶数的回文串(最后可以剩一段无需满足任何条件)。
dp 比较常规。
P4592 [TJOI2018] 异或
solution1
你当然可以直接剖。
solution2
-
询问 dfn 序上的 \([in_u,out_u]\)。
-
询问拆成(祖先到后代链)\([lca,u],[lca,v]\)。
考虑差分,两种询问分开处理,开两棵可持久化字典树。
第一棵维护 dfn 序区间,第二棵维护根到当前点的版本。做完了。
P4602 [CTSC2018] 混合果汁
二分答案。把果汁按美味度排序,\(chk(x)\) 相当于判断只用前 \(x\) 号果汁买 \(L\) 升果汁花的钱是否 \(\le G\)。主席树维护是套路的。Submission。
P11993 [JOIST 2025] 迁移计划 / Migration Plan
很妙,不知道怎么想到的。
考虑合并时不对位合并,而是直接每个深度维护一个集合(合并到当前点的有哪些点),查询时相当于查一个集合中在 \(u\) 的子树内的所有点。考虑使用线段树,以 dfn 序为下标,暴力合并即可。
P5903 【模板】树上 K 级祖先 - 洛谷
长链剖分,设一条链的链长为 \(len\),则在链头维护往上 \(len\) 个点记为 \(up\),往下 \(len\) 个点记为 \(down\)。
对于每个查询,先倍增跳到 \(x\) 的 \(2^{\lfloor \log k\rfloor}\) 级祖先上,此时 \(x\) 的所在链长度一定大于 \(k-2^{\lfloor \log k\rfloor}\)。进一步跳到链头,如果剩余步数是正那么答案为 \(up_{tp,lst}\) 否则为 \(down_{tp,-lst}\)。
复杂度 \(O(n\log n)-O(1)\)。
实现时由于 \(\sum len=n\),所以可以不用 vector,直接使用数组中连续的一段位置。
P12550 [UOI 2025] Reversal ABC
做法参考了 @ Shunpower 的这篇题解。表述比较口语化,不太精简。
solution
结论:交换两个字母之后这两个字母不可能再反向交换回来。
设 \(cnt_{i,c}\) 为长度为 \(i\) 的前缀中有多少个字符 \(c\)。
假设一段里面的字符是 AB,那么划分出这一段的贡献相当于在,这一段内每个 B 的前面有多少个 A(A 也必须在段内),即 \(\sum_{i=l}^{r} [c_i=B](cnt_{i,A}-cnt_{l-1,A})\)。于是进一步设 \(sum_{i,B}\) 表示 \(\sum_{j=1}^{i} [c_j=B]cnt_{j,A}\)。那么一段的贡献就可以表示为:\(sum_{r,B}-sum_{l-1,B}\)。但是此时还多算了 B 在 \([l,r]\) 内但 A 在 \([1,l)\) 的贡献。减去即可(\(cnt_{l-1,A}\times (cnt_{r,B}-cnt_{l-1,B})\))。
\(cnt,sum\) 都可以 \(O(n)\) 预处理求出,于是转移就是 \(O(1)\) 的。
直接做是 \(O(n^2)\) 的。
继续结论:
- 一定不会有一段相同的字符划分到两段中。
- 划分出相邻两段的字符集中的一个完全包含另一个时,一定是不优的。把这两段合并起来贡献不会减少。
有了这两个结论之后可行的转移点个数就变成 \(O(1)\) 的了。
考虑对于一个 \(i\),\(j\) 为最小可以使得 \((j,i]\) 中的字符种类不超过两种的位置。那么 \(j+1\) 一定是一段相同字符的开头。设 \(k\) 为这段相同字符的结尾。此时对于 \(i\) 有效的转移点只有 \(j,k\)。 转移点不可能在 \(j\) 之前;转移点在 \(j\) 之后,\(k\) 之前就把 \((j,k]\) 划分成了两段;转移点在 \(k\) 之后,\((j,k+?]\) 中至少有两种字符,而这两种一定会包含当前段的所有字符。
双指针维护 \(j\),暴力枚举这两种情况即可。最终做到复杂度 \(O(n)\)。
P2465 [SDOI2008] 山贼集团 - 洛谷
感觉思路非常简单自然啊,评高了吧。
solution
\(P\le 12\),考虑状压。
设 \(w_s\) 为一个点同时被集合为 \(s\) 的分部选择的贡献。
设 \(dp_{u,s}\) 为 \(u\) 的子树内(包括本身)放置的分部集合为 \(s\),只考虑 \(u\) 的子树内村庄的贡献,可以得到的最大价值。
对于 \(u\),将一个儿子 \(v\) 的贡献加入的转移为:
枚举 \(x\cup y\),枚举它的子集,复杂度 \(O(3^P)\)。
注意到这里并未计算这些分部对于 \(u\) 本身的贡献,所以还要 \(dp_{u,s}\gets dp_{u,s}+w_s\)。
初始化即把 \(s\) 中的点全部放在 \(u\):\(dp_{u,s}=\sum _{x\in s} a_{u,x}\)。
于是总时间复杂度 \(O(N 3^P)\)。
P1903 [国家集训队] 数颜色 / 维护队列 /【模板】带修莫队
solution
普通莫队带上修改操作。
对于每个操作,增设一个时间维 \(t\) 表示它前面有多少次查询操作。移动时多移动一个时间维即可。
code
这题的实现有一个非常巧妙的地方:当你扫过了一个修改操作,下次再扫回来时应当把这个位置还原。再记一下它原来是什么太复杂了。但是还原这个操作就相当于一个 \(x=a_i\) 的修改操作,于是你发现每次操作时 \(\operatorname{swap}(a_i,x)\) 就可以了。
P4074 [WC2013] 糖果公园
咕了好久的做题记录。
欧拉序(括号序)
对一棵树 dfs 的时候,对于每个点,进入记录一次,出子树时再记录一次,第一次记录时在新序列中的位置记为 \(L_u\)。
性质:对于一对 \((u,v)\),它们路径上除了 lca 之外的所有点,都会在 \((L_u,L_v]\) 中出现 恰好一次。于是支持消掉二次贡献(通常来说是异或)的路径查询就可以转成序列问题了。
solution
加入一个点和删除一个点的贡献都可以 \(O(1)\) 计算。使用上面的 trick,把树搬到序列上,做带修莫队即可。要特判 lca。
P3591 [POI 2015 R3] 访问 Visits
按 \(k\) 分块。对于 \(k\le B\),把 \((u,v)\) 拆成 \((root,u)+(root,v)-2(root,lca)\),预处理 \(sum_{u,k}\) 表示以 \(u\) 为节点,以 \(k\) 为步伐跳到根上的答案。做到 \(O(B)-O(1)\)。
对于 \(k>B\),直接暴力跳。复杂度 \(O(1)-O(B)\)。
需要用长链剖分 \(O(1)\) 求 \(k\) 级祖先。
最终复杂度 \(O(n\sqrt n)\)。难点在于实现,巨量细节。
P1848 [USACO12OPEN] Bookshelf G
设 \(dp_i\) 为考虑了前 \(i\) 本书的答案。
转移:\(dp_i=\min (dp_j+\max_{k=j+1}^{i}h_k)\)。
也就是说,对于单调栈中的一个元素,\(stk_i\) 支配了 \([stk_{i-1},stk_i-1]\) 部分的权值。单调栈套线段树优化即可。
P3645 [APIO2015] 雅加达的摩天楼 - 洛谷
设 \(B=\sqrt n\)。对于一个 \(>B\) 的 \(p\),它能跳到的位置不超过 \(B\) 个。而 \(\le B\) 的 \(p\) 不超过 \(B\) 种。
于是 \((pos,p)\) 的种类数不超过 \(n\sqrt n\) 种。暴力 bfs 即可。需要用 bitset 优化空间。
P4899 [IOI 2018] werewolf 狼人
solution
分别建出 \(w=\min(u,v)\) 的最大 kruskal 重构树,\(w=\max(u,v)\) 的最小 kruscal 重构树。那么对于一个点 \(u\),它能到达的边权不小于 \(L\) 的点就是它最高的点权 \(\le L\) 的祖先的子树内的所有数。\(R\) 的限制在另一棵树上同理。
于是,令 \(S'=S\) 在最大重构树上点权权不小于 \(L\) 的最高祖先,\(T'=T\) 在最小重构树上点权不大于 \(R\) 的最高祖先。我们需要求的就是 \(S'\) 和 \(T'\) 的子树内的叶子是否有交。
注意到子树内的点在 dfs 序中是一段连续的区间,于是把树搬到 dfs 序上。设 \(a\) 为大重构树的 dfs 序,\(b\) 为小重构树的 dfs 序。即判断 \(a_{[L_{S'},R_{S'}]},b_{[L_{T'},R_{T'}]}\) 是否有交。
直接写做法:设 \(p_i\) 为 \(b_i\) 在 \(a\) 中的位置,容易求出。查询即 \(p_{[L_{T'},R_{T'}]}\) 中是否出现了 \([L_{S'},R_{S'}]\) 的数。主席树,或者离线树状数组都可以随便做。
复杂度 \(O(n\log n)\)。
CF2138C2 Maple and Tree Beauty (Hard Version)
solution3
此做法来自@chzhc。
大部分变量名沿用 solution1 部分。
Lemma:如果不能将前 \(m\) 层的节点全部取完,那么答案一定是 \(m-1\)(也就是一定能取完前 \(m-1\) 层)。
证明:
反证法,如果取不完前 \(m-1\) 层,说明第 \(m-1,m\) 层都不能取。
设第 \(m\) 层的节点个数为 \(d\),第 \(m-1\) 层的节点个数为 \(d'\)。显然有 \(d'\le d\)。
设第一个背包用了 \(x\) 的容量(\(x\le k\)),第二个背包用了 \(y\) 的容量(\(y\le n-k\))。
我们有:
\(x+y+d'+d\le n\)
所以,
\(n-x-y\ge d'+d\)
进而,
\(n-x-y\ge 2d'\)
根据抽屉原理,\(k-x\) 和 \(n-k-y\) 中必有一个 \(\ge d'\)。此时将第 \(m-1\) 层的节点放入那个背包即可。取完前 \(m-1\) 层的所有节点。
现在只需要判断能否取完前 \(m\) 层。
设 \(dp_{i,j}\) 表示前 \(i\) 层能否选出一些使得节点个数和为 \(j\)。
转移:\(dp_{i,j}\gets dp_{i-1,j}\vee dp_{i-1,j-a_i}\)。
设 \(sum\) 为前 \(m\) 层的节点个数和。那么两个背包可以空出来的位置的和就是 \(n-sum\)。
第一个背包可以用的合法容量就是 \([k-(n-sum),k]\) 这个区间。因此,只要 \(dp_{n,[k-(n-sum),k]}\) 中任意一个是 \(1\) 答案就是 \(m\),否则答案就是 \(m-1\)。
第一维丢掉,仍然可以 bitset 优化。能过,跟 sol1 没有区别。
此时的转移没有 强制选前 \(i\) 层 这个要求了。所以直接二进制分组优化多重背包就是对的,不需要那一大堆神秘分析。
复杂度还是 \(O(\dfrac{n\sqrt n}{w})\),但常数巨小,不仅好写很多也快很多。
P4562 [JXOI2018] 游戏
考虑求出期望,再乘上总情况数。
定义关键数为 \([L,R]\) 中不是其它数倍数的数。原问题等价于求最后一个关键数的位置,即有多少个非关键数在最后一个关键数后面。
设一共有 \(k\) 个关键数,那么一个非关键数在所有关键数后的概率为 \(\frac{1}{k+1}\),最后一个关键数后非关键数个数的期望为 \((n-k)\frac{1}{k+1}\)。于是答案为 \(\frac{k(n+1)}{k+1}n!\)。
P4083 [USACO17DEC] A Pie for a Pie G
萌萌题。
solution
不妨从每个 \(0\) 开始搜,每次向符合条件的点建边。这样边数显然是 \(O(n^2)\) 的,但是把所有派按照美味值排序后,对于一个点来说,符合条件的点一定是一个区间。
先别急着上线段树!容易发现边权为 \(1\),也就是说,一个点仅会被有效连边一次(即 \(dis\) 最小的来源)。同时,每次 bfs 提出来的点一定是最小的。所以当一个点 \(u\) 可以更新另一个点 \(v\) 时,\(v\) 在后面一定不会被更新了。所以用 set 维护还没被更新的点的集合,每次暴力扫过去,更新一些点然后把它们删掉。复杂度 \(O(n\log n)\)。
P3639 [APIO2013] 道路费用
难写题。
solution
\(k\le 20\),考虑枚举每条新边选不选。
枚举后再跑最小生成树肯定爆炸。观察到生成树的大多数边都没有变化,考虑先固定住一些不变的边。
具体来说,先把新边全部加入生成树,再跑最小生成树。我们第二次加入的 \(n-1-k\) 条边就一定在各种情况下都存在于生成树上,假设这个“树”为 \(T\)。用这 \(n-1-k\) 条边建出生成树,再加旧边跑生成树,跑出来的 \(k\) 条旧边就是可能会出现在生成树上的边,设这个集合为 \(A\)。其余的边不需要再考虑。
每次枚举一个新边集合,将它们加入 \(T\)。再枚举 \(A\) 中的边加入,我们就得到了强制选这个新边集合的生成树形态。接下来考虑边权有什么限制。容易发现,如果 \(A\) 中存在一条边 \((u,v,w)\),且这条边没有被选入当前生成树,那么生成树中 \((u,v)\) 路径上的所有边都必须要满足边权 \(\le w\)。同时也不会有比这更严格的限制,因为不可能选剩余的其它边而不选 \(A\) 中的边。
模拟上面的东西即可。复杂度 \(O(m\log m+2^k k^2)\)。
P7984 [USACO21DEC] Tickets P
比较直接的双老哥做法。
solution
对于每个点都求到 \(1,n\) 的最短路太困难了,考虑(建反图)转而求 \(1,n\) 到每个点的最短路。分别求出 \(1,n\) 到每个点的最短路,记为 \(dis\) 和 \(dis'\)。那么对于每个点 \(u\) 来说答案的上界就是 \(dis_u+dis_u'\)。
考虑什么时候会算多。那么一定是走了一段相同的路,付了两次钱。
同时我们断言,这一段相同的路只会是最后一段(而不可能在前面有其它段走了相同的路),形如 Y 型(下图)。
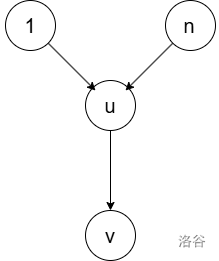
证明比较显然:如果在更前的地方走了一段相同的,后面再分叉,一定不如直接一起走到终点。
于是答案式子为:\(ans_v=\min\{dis_v+dis_v',\min_u (ans_u+w_{u,v})\}\)。
这仍然是一个最短路的形式。所以在求完 \(dis,dis'\) 后,从一个超级源点向所有点建边权为 \(dis+dis'\) 的边,再跑一次最短路即可求出答案。
现在只需要解决一个区间向一个点连边,求最短路的问题。线段树优化建图即可。
复杂度 \(O(n\log^2 n)\)。
code
非常需要注意的是,你需要给每张票建一个虚点,而不是直接把一个区间连向买票的点,否则因为线段树把这个区间拆成了很多小区间,你可能会给每个小区间额外付一次费。详见:@ MeowScore 的警示帖。
P3232 [HNOI2013] 游走
因为到 \(n\) 就结束了,所以下文中的点默认不包含 \(n\)。
设 \(f_u\) 为点 \(u\) 的期望经过次数,\(g_e\) 为边 \(e\) 的期望经过次数。
那么总分期望 \(=\sum g_ew_e\),其中 \(w\) 是边权。
所以只需要求出所有的 \(g\),按照 \(g\) 的大小分配边权就可以求出答案。
\(g\) 还是不太好求,将它转化为 \(f\)。
对于一条边 \(e(u,v)\),我们有:\(g_e=\frac{1}{deg_u}f_u+\frac{1}{deg_v}f_v\)。
\(f\) 的式子就比较直观了:\(f_u=\sum_{(u,v)\in E} \frac{1}{deg_v}f_v\)。
由于 \(n\le 500\),所以直接高斯消元就可以做了!
复杂度 \(O(n^3)\)。
P4550 收集邮票
设 \(f_i\) 表示已经拥有了 \(i\) 张邮票,还需要购买次数的期望;\(g_i\) 为还需要花费钱数的期望。
\(f_i=\frac{i}{n}f_i+\frac{n-i}{n}f_{i+1}+1\),
\(g_i=\frac{i}{n}(g_i+f_i)+\frac{n-i}{n}(g_{i+1}+f_{i+1})+1\)。
其中 \(g\) 的推导运用了类似费用提前计算的 trick,每次购买累加当前和后面的贡献。
最佳策略(strategy)
题面存档。非常好的题目。
solution
设 \(dp_{i,j}\) 为割完前 \(i\) 块草坪,现在割草机使用了 \(j\) 的容量,花费时间的最小值。
设 \(tmp\) 为若割草机为空,当前草坪所需要花费的总时间(不强制清空)。
对于 \(v_i\bmod c\) 进行分类讨论:
- $v_i\equiv0\pmod c $
- $v_i\not \equiv 0\pmod c $
最后可以花 \(b\) 的代价清空:\(dp_{i,0}\gets \min dp_{i,j}+b\)。
转移式子手推一下不难理解。
第一种情况处理是简单的!一棵区间加,单点修的线段树即可。
观察一下第二种情况。注意到下标都进行了 \(+(v_i\bmod c)\) 的偏移(如果 \(\ge c\) 就从 \(0\) 开始依次编号)。这个东西可以套路地打区间偏移量(具体来说就是记录当前的 \(0\) 在原来的哪个位置)标记做。假设现在的 \(0\) 偏移到了 \(L\),那么区间就被拆成了 \([L,c-1][0,c-2]\) 两部分。把区间操作也拆成这两个部分的分别做即可。
复杂度 \(O(n\log V)\)。
NOIP模拟赛 表白(love)
模拟赛题,感觉很有意义。
description
给你一个长度为 \(n\) 的序列 \(a\),定义选出一些数的权值为 \((\prod a)\bmod m\)。\(q\) 次询问,每次求一个区间 \([l,r]\) 能选出的最大权值。\(n,q\le 10^5,m\le 521\)。
solution
设 \(dp_{i,j}\) 为以 \(i\) 为右端点,能够凑出 \(j\) 的最大左端点。
查询时从大到小枚举答案,遇到的第一个 \(dp_{r,j}\ge l\) 的 \(j\) 就是答案。
复杂度 \(O(nm)\)。可以离线然后滚掉一维数组。
CF804D Expected diameter of a tree
solution
显然无解情况会出现当且仅当 \(a,b\) 在同一棵树上。接下来不讨论。
假设 \(a\) 在 \(T1\) 这棵树上,\(b\) 在 \(T2\) 这棵树上。那么答案就是 \(T1,T2\) 分别任意选一点 \(u,v\),连接 \(u,v\) 后新树的直径长度和除以情况总数(\(siz_{T1}\times siz_{T2}\))。
设 \(D_i\) 为一棵树 \(i\) 的直径,\(f_u\) 为点 \(u\) 在它原本的树中到距离最远的点的距离。
设 \(d'=\max(D_{T1},D_{T2})\),显然 \(d'\) 是一个常量。
那么对于一对 \((u,v)\),连接它们后新树 \(T\) 的直径 \(D_T=\max(d',f_u+f_v+1)\)。
此时枚举 \(f_u\),分类讨论 \(f_v\) 的情况:
- \(f_v\le d'-f_u-1\):此时 \(D_T=d'\)。即一个 \(v\) 对于答案的贡献是 \(d'\)。
- \(\text{otherwise}\):此时 \(D_T=f_u+f_v+1\)。同。
容易发现只需要知道 \(f_v\) 在一个范围内的个数、\(f_v\) 的和。前缀和可以做到 \(O(n)\) 预处理,\(O(1)\) 查询。
这样做的单次查询的复杂度是 \(O(\max_{u\in T1} f_u)\) 的。于是我们钦定 \(\max_{u\in T1} f_u\le \max_{v\in T2} f_v\),这样复杂度显然更优。
但如果 \(\max f_u\) 很大就爆炸了。
考虑根号分治的思想:\(\max f_u \ge \sqrt n\) 的连通块数量不超过 \(\sqrt n\) 个。也就是说,对于每棵 \(\max f_u\ge \sqrt n\) 的树,因为我们钦定了 \(\max f_u\) 是两树中较小的一个,所以合法的 \(T2\) 个数是 \(O(\sqrt n)\) 的。于是对于一个 \(T1\) 做到复杂度 \(O((\max_{u\in T1} f_u)\times \sqrt n)\)。总复杂度为 \(O(\sum(\max f_u)\times n)\),其中 \(\sum f\) 显然 \(O(n)\),于是做到 \(O(n\sqrt n)\)。
剩下 \(\max f_u<\sqrt n\) 的情况暴力做,复杂度 \(O(q\sqrt n)\)。
于是对于每个 \((T1,T2)\) 记录答案,记过答案的直接输出,没记过的直接做即可做到根号复杂度。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号