qoj1268 D. Diamond Rush 题解

solution

step1

考虑怎么刻画“不经过一个矩形”。

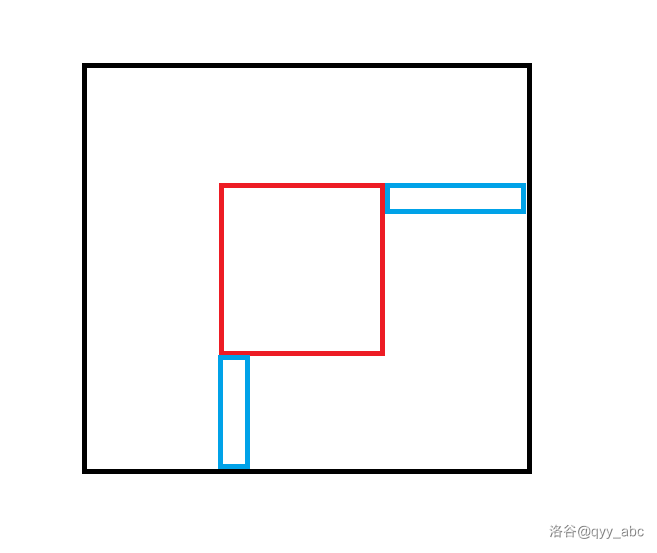
如图，发现不经过红色矩形就等价于必须经过两个蓝色矩形其中之一。

我们只需要对于每个点递推出从左上到它的答案和右下到它的答案，将每个点的两部分拼起来。查询时在蓝色矩形的点中找最大的答案就可以保证限制了。

step2

因为数值过大，算答案时直接比大小肯定是不行的。

观察发现，给出的点权相当于 \(n^2\) 进制上有且只有一位为 \(1\) 的数，保证计算过程中没有进位（进位需要 \(n^2\) 个相同的数，但我们总共只有 \(n^2\) 个数）。

类似 \(n^2\) 进制高精度，需要的操作有：

• 比大小
• 在某个位置上 \(+1\)

考虑主席树。第二个操作非常显然。第一个操作可以维护哈希值，在树中找到最大的不一样的位置，比较那一位的大小。

corner case

• “拼起来”这部分不能线段树合并（这样复杂度就 \(O(n^3 \log {n^2})\) 了！），考虑哈希值可以相加，所以比大小时直接同时传两个根进去，用到了再合并哈希值，其它一样做就行了。
• 需要预处理出对于每一个点来说两个方向的蓝色矩形的答案（前/后缀max）。这样查询的时候直接比较两个蓝色矩形的最大值（两颗主席树）的大小就可以了。

复杂度 \(O(n^2 \log n^2+q \log n^2)\)，常数好像非常巨大。但是比起 \(O(n^3)\) 还是飞快，不用卡常。

code

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
int _;
const int maxn=403,maxv=maxn*maxn;
int n,q;
int a[maxn][maxn];
int xe,ye,xy,yy;
const int mod=531902729;
inline int ad(int qye,int qyy){qye+=qyy;return qye>=mod?qye-mod:qye;}
const int md=1e9+7;
inline void adtm(int &qye,int qyy){((qye+=qyy)>=md)&&(qye-=md);}
const int p_=13331;
int pw[maxv],pwn[maxv];
namespace Segtree{
	int liz;
	int rt[maxn][maxn][2];
	struct node{
		int ls,rs;
		int h;//哈希值 
	}tr[maxv<<7];
	#define mid (l+r>>1)
	#define ls(x) tr[x].ls
	#define rs(x) tr[x].rs
	#define lsi(x) ls(x),l,mid
	#define rsi(x) rs(x),mid+1,r
	#define h(x) tr[x].h
	inline void pushu(int p,int l,int r){h(p)=ad(1ll*h(ls(p))*pw[r-mid]%mod,h(rs(p)));}
	void upd(int &p,int l,int r,int loc){
		tr[++liz]=tr[p];p=liz;
		if(l==r){tr[p].h++;return;}
		if(loc<=mid) upd(lsi(p),loc);
		else upd(rsi(p),loc);
		pushu(p,l,r);
	}
	void updj(int &p,int l,int r,int loc){
		tr[++liz]=tr[p];p=liz;
		if(l==r){tr[p].h--;return;}
		if(loc<=mid) updj(lsi(p),loc);
		else updj(rsi(p),loc);
		pushu(p,l,r);
	}
	bool dy(int p1,int p2,int l,int r){//p1>p2
		if(h(p1)==h(p2)) return 0;
		if(l==r) return h(p1)>h(p2);
		if(h(rs(p1))^h(rs(p2))) return dy(rs(p1),rs(p2),mid+1,r);
		return dy(ls(p1),ls(p2),l,mid);
	}
	bool dy2(int p1,int p2,int p3,int p4,int l,int r){//p1+p2>p3+p4?
		if(ad(h(p1),h(p2))==ad(h(p3),h(p4))) return 0;
		if(l==r) return h(p1)+h(p2)>h(p3)+h(p4);
		if(ad(h(rs(p1)),h(rs(p2)))^ad(h(rs(p3)),h(rs(p4)))) return dy2(rs(p1),rs(p2),rs(p3),rs(p4),mid+1,r);
		return dy2(ls(p1),ls(p2),ls(p3),ls(p4),l,mid);
	}
}using namespace Segtree;
int dp[maxn][maxn][2];//左上/右下到它的答案 
#define pii pair<int,int>
pii cr[maxn][maxn],vr[maxn][maxn];/*对于每个点来说横/竖蓝色矩形的根*/ 
int ac[maxn][maxn],av[maxn][maxn];/*对于每个点来说横/竖蓝色矩形的答案*/ 
#define fi first
#define se second
#define mkp make_pair
const pii emp=mkp(0,0);
signed main(){
	ios::sync_with_stdio(0);
	cin.tie(0);cout.tie(0);
	cin>>_;
	pw[0]=pwn[0]=1;for(int i=1;i<maxv;i++) pw[i]=1ll*pw[i-1]*p_%mod;
	while(_--){
		cin>>n>>q;int nn=n*n;
		for(int i=1;i<=nn;i++) pwn[i]=1ll*pwn[i-1]*nn%md;
		for(int i=1;i<=n;i++) for(int j=1;j<=n;j++) cin>>a[i][j];
		liz=0;
		for(int i=0;i<=n+1;i++) rt[i][0][0]=rt[i][n+1][0]=rt[0][i][0]=rt[n+1][i][0]=0;
		for(int i=0;i<=n+1;i++) dp[i][0][0]=dp[i][n+1][0]=dp[0][i][0]=dp[n+1][i][0]=0;
		for(int i=1;i<=n;i++){
			for(int j=1;j<=n;j++){
				if(dy(rt[i-1][j][0],rt[i][j-1][0],1,nn)){rt[i][j][0]=rt[i-1][j][0];dp[i][j][0]=dp[i-1][j][0];}
				else{rt[i][j][0]=rt[i][j-1][0];dp[i][j][0]=dp[i][j-1][0];}
				adtm(dp[i][j][0],pwn[a[i][j]]);
				upd(rt[i][j][0],1,nn,a[i][j]);
			}
		}//左上到它 
		for(int i=0;i<=n+1;i++) rt[i][0][1]=rt[i][n+1][1]=rt[0][i][1]=rt[n+1][i][1]=0;
		for(int i=0;i<=n+1;i++) dp[i][0][1]=dp[i][n+1][1]=dp[0][i][1]=dp[n+1][i][1]=0;
		for(int i=n;i>=1;i--){
			for(int j=n;j>=1;j--){
				if(dy(rt[i+1][j][1],rt[i][j+1][1],1,nn)){rt[i][j][1]=rt[i+1][j][1];dp[i][j][1]=dp[i+1][j][1];}
				else{rt[i][j][1]=rt[i][j+1][1];dp[i][j][1]=dp[i][j+1][1];}
				adtm(dp[i][j][1],pwn[a[i][j]]);
				upd(rt[i][j][1],1,nn,a[i][j]);
			}
		}//右下到它 
		for(int i=n;i>=1;i--) for(int j=n;j>=1;j--) updj(rt[i][j][1],1,nn,a[i][j]),adtm(dp[i][j][1],md-pwn[a[i][j]]);
		for(int i=0;i<=n+1;i++) cr[i][n+1]=vr[n+1][i]=emp;
		for(int i=0;i<=n+1;i++) ac[i][n+1]=av[n+1][i]=0;
		for(int i=1;i<=n;i++){
			for(int j=n;j>=1;j--){
				if(dy2(cr[i][j+1].fi,cr[i][j+1].se,rt[i][j][0],rt[i][j][1],1,nn)){cr[i][j]=cr[i][j+1];ac[i][j]=ac[i][j+1];}
				else{cr[i][j]=mkp(rt[i][j][0],rt[i][j][1]);ac[i][j]=(dp[i][j][0]+dp[i][j][1])%md;}
				if(dy2(vr[j+1][i].fi,vr[j+1][i].se,rt[j][i][0],rt[j][i][1],1,nn)){vr[j][i]=vr[j+1][i];av[j][i]=av[j+1][i];}
				else{vr[j][i]=mkp(rt[j][i][0],rt[j][i][1]);av[j][i]=(dp[j][i][0]+dp[j][i][1])%md;}
			}
		}//求蓝色矩形最大答案 
		for(int i=1;i<=q;i++){
			cin>>xe>>xy>>ye>>yy;xe--,ye--,xy++,yy++;
			//比较取哪个矩形 
			if(dy2(cr[xe][yy].fi,cr[xe][yy].se,vr[xy][ye].fi,vr[xy][ye].se,1,nn)) cout<<ac[xe][yy]<<'\n';
			else cout<<av[xy][ye]<<'\n';
		}
	}
	return 0;
}