网络流杂记
浅记一下kk。
以下默认:
- \(S\) 为源点,\(T\) 为汇点。
- \(dis(x)\) 为源点到 \(x\) 的(费用)最短路
- 待定。
最大流
初始无负权最小费用最大流(lg P3381 【模板】最小费用最大流)
在流量为正的边上跑最短路,在最短路上找出一条增广路(反边的代价是 \(-c\))。这里不展开了,详细的还是费用流 - OI Wiki!
常规写法找最短路是 SPFA(反边是负权),但 SPFA 复杂度波动太大了。提供一个可以用 Dijkstra 的方法。找增广路的部分是一样的。
Johnson Reweighting
定义新边权 \(w'=w+h(u)-h(v)\),\(h(x)\) 是一个函数。
- 新的最短路 \(dis'(x)=dis(x)+h(s)-h(x)\),所以如果求出了 \(dis'\) 就可以倒推出 \(dis\)。
取 \(h(x)=dis(x)\),我们有:
- 边权非负(\(h(v) \le h(u)+w\)),可以直接 dij。
- 在最短路上的边一定满足 \(w'=0\)
但用一个最短路的函数来求最短路不是搞笑吗?
一个更有用的性质:由于第一轮的反边流量都是 \(0\) 所以不影响最短路,现在会受影响的只有在网络流过程中增加出的反边上的负花费。网络流建出的反边,一定在最短路上。而在最短路上的边满足 \(w'=0\)。我们证明出来新建出来的边不会对 dij 的正确性产生任何影响!因此可以直接用上一轮求出的 \(dis(x)\) 当 \(h(x)\) 。
考虑怎么更新。因为 \(dis(x)=dis'(x)-h(s)+h(x)\),\(h(s)=0\),所以 \(dis(x)=dis'(x)+h(x)\)。每次更新时只要把本轮的 \(dis'(x)\) 加到 \(h(x)\) 就得出了新一轮的 \(h(x)\)(即 \(dis(x)\))。
时间复杂度 \(O(F (n+m) \log n)\),跑得相当快。
保证初始无负环的情况下都可以用(初始有负权的情况,可以第一轮用 SPFA 求出 \(h(x)\))。
code
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
template<typename diz> inline void chkn(diz &qye,diz qyy){qye=min(qye,qyy);}
template<typename diz> inline void chkx(diz &qye,diz qyy){qye=max(qye,qyy);}
const int maxn=5006,maxm=50006;
const int inf=1e9+101121;
int n,m,s_,t_;
struct Edge{int to,nxt,f,c;/*f是流量,c是费用*/}edg[maxm<<1];
int hd[maxn],tt=1;
inline void add(int u,int v,int f,int c){edg[++tt]={v,hd[u],f,c};hd[u]=tt;}
int h[maxn];
int dis[maxn];bool vis[maxn];
struct node{
int u,dis;
bool operator <(const node &qyy)const{return dis>qyy.dis;}
};
int fr[maxn];
inline bool dijkstra(){
priority_queue <node> pq;
for(int i=1;i<=n;i++) dis[i]=inf,vis[i]=0;
pq.push({s_,dis[s_]=0});
while(pq.size()){
int u=pq.top().u;pq.pop();
if(vis[u]) continue;vis[u]=1;
for(int e=hd[u],v,di;e;e=edg[e].nxt){
v=edg[e].to;
if(edg[e].f&&!vis[v]){
di=dis[u]+h[u]-h[v]+edg[e].c;
if(di<dis[v]){dis[v]=di;pq.push({v,di});fr[v]=e;}
}
}
}
return dis[t_]>=inf?0:1;
}
int ansf,ansc;
inline void solve(){
int diz=inf;
for(int u=t_;u^s_;u=edg[fr[u]^1].to) chkn(diz,edg[fr[u]].f);
ansf+=diz;
for(int u=t_;u^s_;u=edg[fr[u]^1].to) edg[fr[u]].f-=diz,edg[fr[u]^1].f+=diz,ansc+=edg[fr[u]].c*diz;
for(int i=1;i<=n;i++) if(dis[i]<inf) h[i]+=dis[i];
}
signed main(){
ios::sync_with_stdio(0);
cin.tie(0);cout.tie(0);
cin>>n>>m>>s_>>t_;
for(int i=1,u,v,f,c;i<=m;i++){
cin>>u>>v>>f>>c;
add(u,v,f,c);add(v,u,0,-c);
}
while(dijkstra()) solve();
cout<<ansf<<' '<<ansc<<'\n';
return 0;
}
无源汇有上下界可行流 (loj#115. 无源汇有上下界可行流)
对于每条边 \((u,v,l,r)\),先让其强制流完 \(l\) 的流量,它就变成了 \((u,v,0,r-l)\),即普通最大流。
但“强制流完”可能会令原图的一些点不满足流量平衡。我们定义 \(w_i\) 为点 \(i\) 流入(如果是负就是流出)了多少流量。
我们设一个源点 \(s\) 和汇点 \(t\)。
对于每个 \(i\):
- \(w_i=0\):不理它。
- \(w_i>0\):此时这个点多流入了流量。我们让 \(s\) 来流这些流量,即连边 \((s,i,w_i)\)。
- \(w_i<0\):同理让这些流量流去 \(t\),即连边 \((i,t,-w_i)\)。
对新建出的这张图跑最大流。当我们对 \(s\)(或 \(t\),流量是守恒的)建的边流满时说明存在可行解满足原题所有约束。设求出最大流为 \(ans\),即 \(ans \ge \sum w_i[w_i>0]\) 时,原问题存在可行解。
code
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn=206,maxm=10205;
const ll inf=1e15+101121;
int n,m,diz_,rzf_;
namespace Graph{
struct Edge{int to,nxt,w;}edg[maxm<<2];
int id[maxm];
int hd[maxn],tt=1;
inline void add(int u,int v,int w){edg[++tt]={v,hd[u],w};hd[u]=tt;}
inline void adde(int u,int v,int w){add(u,v,w);add(v,u,0);}
int a[maxn];
int ans[maxm];
inline void ade(int u,int v,int l,int r,int i){
adde(u,v,r-l);id[i]=tt;//反边id
ans[i]=l;//强制流l的流量
a[u]-=l,a[v]+=l;//流入/流出
}
}using namespace Graph;
namespace Dicnic{
int dep[maxn],nw[maxn];
inline bool bfs(){
queue <int> pq;pq.push(diz_);
memset(dep,0x3f,sizeof(dep));
dep[diz_]=0;nw[diz_]=hd[diz_];
while(!pq.empty()){
int u=pq.front();pq.pop();
for(int e=hd[u];e;e=edg[e].nxt){
int v=edg[e].to;
if(edg[e].w&&dep[v]==dep[0]){
dep[v]=dep[u]+1;nw[v]=hd[v];
if(v==rzf_) return 1;
pq.push(v);
}
}
}
return 0;
}
ll ansl;
ll dfs(int u,ll lst){
if(u==rzf_) return lst;
ll res=0;
for(int e=nw[u];lst&&e;nw[u]=e=edg[e].nxt){
int v=edg[e].to;
if(edg[e].w&&(dep[v]==dep[u]+1)){
ll cur=dfs(v,min(lst,(ll)edg[e].w));
if(!cur){dep[v]=dep[0];continue;}
edg[e].w-=cur,edg[e^1].w+=cur;
res+=cur,lst-=cur;
}
}
return res;
}
}using namespace Dicnic;
signed main(){
ios::sync_with_stdio(0);
cin.tie(0);cout.tie(0);
cin>>n>>m;
for(int i=1,u,v,l,r;i<=m;i++){cin>>u>>v>>l>>r;ade(u,v,l,r,i);}
diz_=n+1,rzf_=n+2;
for(int u=1;u<=n;u++){
if(!a[u]) continue;
if(a[u]<0) adde(u,rzf_,-a[u]);
else adde(diz_,u,a[u]),ansl-=a[u]/*-sum*/;
//建图
}
while(bfs()) ansl+=dfs(diz_,inf);
if(ansl>=0){
cout<<"YES\n";
for(int i=1;i<=m;i++) cout<<ans[i]+edg[id[i]].w<<'\n';
}
else cout<<"NO\n";
return 0;
}
有源汇有上下界可行流
加入一条边 \((t,s,0,+\infty)\),问题转化为无源汇上下界可行流。
此时 \(s\) 到 \(t\) 的流量为 \(t\) 到 \(s\) 反边的流量,因为 \(s\) 除此没有其它入边(\(t\) 没有其它出边)。
有源汇上下界最大流(loj#116. 有源汇有上下界最大流)
在上一个的基础上找出最大流。
先跑一遍可行流,无解就结束。
删掉我们额外添加的边,在剩余网络中跑最大流。因为边权是处理过的且跑最大流流量一定平衡,所以结果一定满足约束。
最后可行流和最大流的流量相加就是答案。
有负权费用流(luoguP7173 【模板】有负圈的费用流)
前面的铺垫都是为了这个!太牛了!!
初始可能有负环,无法直接跑费用流。
如果负权边一开始流满,就变成了初始没有负权的情况。“强制流满”刚在上下限中用过,所以使用几乎一样的方法就可以了!
详细一点来说,对于费用 \(c_i < 0\) 的边,按照前面处理将它强制流满。不同的是需要建反边用于退流(下面有详细解释!)。
在新图上跑一遍费用流,删掉多添加的边(和点)后再跑一遍费用流,答案相加即可。
其实到这已经结束了,挂两个一开始不理解的弱智问题。
- 为什么不会跑出上下限网络流中“可行流不存在”的问题?
因为只是先流满(以去掉负权边),而不是真的强制流满,所以需要建反向边用于退流。有反边的情况下自然有可行流。
- 跑完可行流之后可能会有负权边,如何保证没有负环?
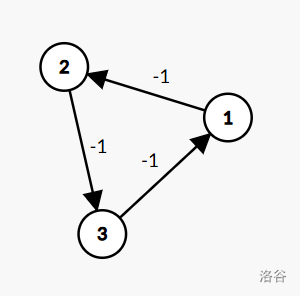
这个问题实在是好蠢。考虑一个负环:
原图长这样:
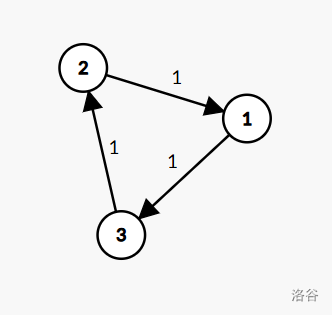
要让它们跑完边权都是负数,只能每条边都正着跑一次。
从一个点跑过一个正环回到原点肯定是不优的。
而如果从一个点到另一个点,跑一条路使得出现负环,说明环上剩下的边都已经是负边,那一定走环上的另一边更优。
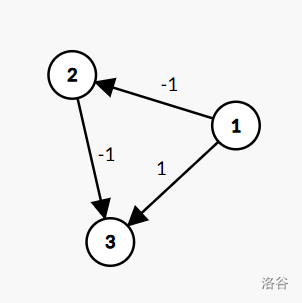
语言能力过于低下感性理解。比如说前面跑了几次把图跑成这样:
此时从 \(1\) 到 \(3\) 走两条负边一定更优。
code
其实就是把上下限和费用流拼起来。
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
template<typename diz> inline void chkn(diz &qye,diz qyy){qye=min(qye,qyy);}
template<typename diz> inline void chkx(diz &qye,diz qyy){qye=max(qye,qyy);}
/*diz /ka/ka*/
const int maxn=5006,maxm=50006;
const int inf=1e9+101121;
int n,m,s,t;
int ansf,ansc;
struct Edge{int to,nxt,f,c;}edg[maxm<<1];
int hd[maxn],tt=1;
inline void add(int u,int v,int f,int c){edg[++tt]={v,hd[u],f,c};hd[u]=tt;}
inline void adde(int u,int v,int f,int c){add(u,v,f,c);add(v,u,0,-c);}
int a[maxn];
inline void ade(int u,int v,int f,int c){
adde(v,u,f,-c);//反边用于退流
a[u]-=f,a[v]+=f;
ansc+=c*f;
}
int h[maxn];
int dis[maxn];bool vis[maxn];
struct node{
int u,dis;
bool operator <(const node &qyy)const{return dis>qyy.dis;}
};
int s_,t_;
inline void spfa(){
queue <int> pq;
for(int i=1;i<=n;i++) h[i]=inf,vis[i]=0;
pq.push(s_);h[s_]=0,vis[s_]=1;
while(pq.size()){
int u=pq.front();pq.pop();vis[u]=0;
for(int e=hd[u],v;e;e=edg[e].nxt){
v=edg[e].to;
if(edg[e].f&&h[v]<h[u]+edg[e].c){
h[v]=h[u]+edg[e].c;
if(!vis[v]) pq.push(v),vis[v]=1;
}
}
}
}
int fr[maxn];
inline bool dijkstra(){
priority_queue <node> pq;
for(int i=1;i<=n;i++) dis[i]=inf,vis[i]=0;
pq.push({s_,dis[s_]=0});
while(pq.size()){
int u=pq.top().u;pq.pop();
if(vis[u]) continue;vis[u]=1;
for(int e=hd[u],v,di;e;e=edg[e].nxt){
v=edg[e].to;
if(edg[e].f&&!vis[v]){
di=dis[u]+h[u]-h[v]+edg[e].c;
if(di<dis[v]){dis[v]=di;pq.push({v,di});fr[v]=e;}
}
}
}
return dis[t_]>=inf?0:1;
}
inline void solve(){
int diz=inf;
for(int u=t_;u^s_;u=edg[fr[u]^1].to) chkn(diz,edg[fr[u]].f);
ansf+=diz;
for(int u=t_;u^s_;u=edg[fr[u]^1].to) edg[fr[u]].f-=diz,edg[fr[u]^1].f+=diz,ansc+=edg[fr[u]].c*diz;
for(int i=1;i<=n;i++) if(dis[i]<inf) h[i]+=dis[i];
}
void sol(int s,int t){
s_=s,t_=t;
spfa();//求出第一轮h(x)
while(dijkstra()) solve();
}
signed main(){
ios::sync_with_stdio(0);
cin.tie(0);cout.tie(0);
cin>>n>>m>>s>>t;
for(int i=1,u,v,f,c;i<=m;i++){
cin>>u>>v>>f>>c;
if(c>=0) adde(u,v,f,c);
else ade(u,v,f,c);
}
const int aaa=tt;
adde(t,s,inf,0);
int ss=n+1,st=n+2;
for(int u=1;u<=n;u++){
if(!a[u]) continue;
if(a[u]>0) adde(ss,u,a[u],0);
else adde(u,st,-a[u],0);
}
n+=2;
sol(ss,st);
n-=2;
ansf=edg[aaa+2].f;//可行流
for(int e=aaa+1;e<=tt;e++) edg[e].f=0;//删掉后加的边
sol(s,t);
cout<<ansf<<' '<<ansc<<'\n';
return 0;
}
完结撒花!




 浙公网安备 33010602011771号
浙公网安备 33010602011771号