斜率优化

25.08.21

前置芝士：凸包（虽然好像没那么重要）

凸多边形：凸多边形是指所有内角大小都在
\([0,\pi]\) 范围内的 简单多边形。

凸包：在平面上能包含所有给定点的最小凸多边形叫做凸包。

其实就是用一个橡皮筋捆住所有给定点的那根橡皮筋围起来的那个东西。（引自 oi-wiki 相关部分)

考虑一个朴素的一维 dp 转移方程（\(f(j)\) 是有关 \(dp_j\) 和 \(j\) 的柿子）：

\[dp_i=\min f(j)+w(i,j) \]

斜率优化的思想是这样的：

1. 考虑直线斜截式 \(y=kx+b\)，即 \(b=y-kx\).
2. 分离 \(w(i,j)\)，将转移方程写为 \(g(i)=f(j)+p(i)\times q(j).\)
3. 应用 \(b=y-kx\)，令 \(b=g(i),y=f(j),k=-p(i),x=q(j)\)，则天然地一个关于 \(j\) 的状态就可以表示为一个点 \((q(j),f(j))\)，向 \(i\) 的转移就是求经过某一点的斜率为 \(-p(i)\) 的直线的最小/最大截距。

现在问题变成了一道几何题，我们画图来考虑。（抄了 oi-wiki 的图）

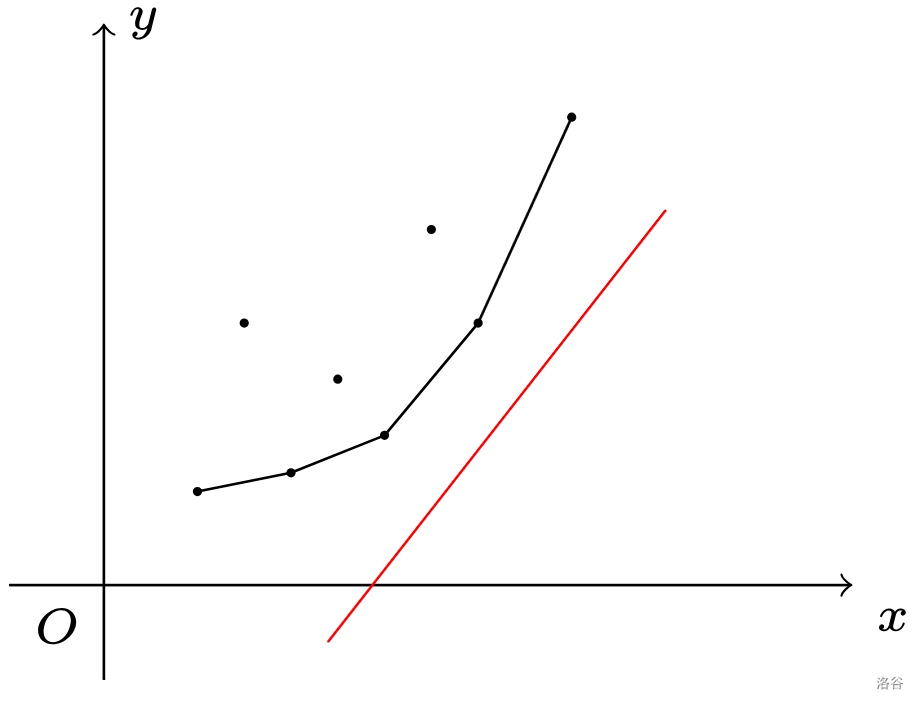
以下都以最终转移目标为使截距最小为例，最大时同理。

对于所有的可能转移到 \(i\) 的所有 \(j\) 形成的那个下凸壳，我们要使得截距最小，必然是用那根定斜率直线去切 Ta，即不断将这跟直线从下往上平移直到经过下凸壳的一个顶点。

如果这个下凸壳有着较好的性质，比如像上面这个图一样，壳上的相邻两点斜率单调递增，我们就可以用单调队列维护这个凸壳。

而且，这样的凸壳对决策也很好，我们只需要找到壳上的一个点 \(e\) 满足 \(k_{e-1,e}\le k_i<k_{e,e+1}\) 就好了（观察上面的图就能发现这一点）。具体实现若关于 \(i\) 的斜率函数具有单调性就可以直接把用不到的壳从单调队列里弹出，否则只能完整地存下整个壳，每次二分去找。

如果觉得上面这些话说得太抽象了，下面是不那么抽象的代数证明：

考虑一个化简完毕的 dp 柿子：\(dp_i+c_i=a_i\times b_j+d_j\), 任意掏出两个决策点 \(j_1,j_2\), 下面我们将比较 Ta 们之间的优劣 (下面考虑的都是取 \(\min\) 的情况)。

不妨令 \(dp(j_1)<dp(j_2)\), 则有：

\[a_i\times b_{j_1}+d_{j_1}<a_i\times b_{j_2}+d_{j_2} \]

令 \(Y(j)=-d_j,X(j)=b_j\), 则：

\[a_i>\frac{Y(j_2)-Y(j_1)}{X(j_2)-X(j_1)} \]

综上，对于两个决策点，如果 Ta 们之间的斜率小于 \(i\) 对应的斜率函数值，后面的点优于前面的点。

接下来考虑三个点, \(k_{2,3}<k_{1,2}\).

• 若 \(k<k_{2,3}<k_{1,2}\), 则 \(A\) 优于 \(B\), \(B\) 优于 \(C\)。
• 若 \(k_{2,3}\le k\le k_{1,2}\), 则 \(A\) 优于 \(B\), \(C\) 优于 \(B\)。
• 若 \(k_{2,3}<k_{1,2}<k\), 则 \(B\) 优于 \(A\), \(C\) 优于 \(B\)。

无论何种情况, \(B\) 都不是最优，所以这就证明了最优决策点必定构成下凸壳。实现时这时候就会把 \(B\) 踹出单调队列。

注意：

1. 在新加入一个点时，应该让这个点和下凸壳最靠右的点连线，若其斜率不满足单调性，弹出最右点，重复上述过程。不是拿这个点和前面某个点的斜率一直在单调队列里干什么事情（话说到底是谁会出现这种错误）。
2. 当你把转移方程化为斜率优化形式的时候，一定要注意你前面的是 \(y\)，后面的才是 \(x\)。存到point里的时候一定不要写反了。

斜率优化的进阶应用是将斜率优化与二分/分治/数据结构等结合，来维护性质不那么好（缺少一些单调性性质）的 DP 方程，等我学了再往后写。