树状数组 & 线段树

写于 2023.11

树状数组

树状数组是维护 \(n\) 个数的前缀信息的一维数组。

其树型结构如下

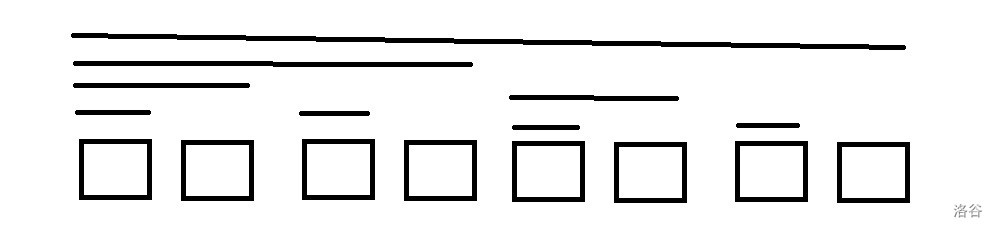
这样的结构有着写法简单，常数小的特点。

其模板代码如下：

inline int lowbit(const int &x){//最后一个 '1' 对应的值 
	return x&-x;
}
void add(int pos,int val){//单点修改,将 a[pos] 的值增加 val 
	while(pos<=n) t[pos]+=val,pos+=lowbit(pos);
}
int query(int pos){//查询[1,pos]的和 
	int sum=0;
	while(pos) sum+=t[pos],pos-=lowbit(pos);
	return sum;
}

除发挥其原本的前缀维护功能外( \(O(logn)\) 的前缀查询与单点修改)，还可以用它来维护一个差分数组。这样，前缀和查询就变为了修改后的值的查询，弥补了差分数组只能“多次操作，一次查询”的短板。

将调用部分稍作修改即可完成 \(O(logn)\) 的区间修改与单点查询。

//此处t数组实际为一个差分数组
//[l,r]+val
add(l,val),add(r+1,-val);
//query: pos
printf("%d\n",query(pos));

其实，树状数组还可以方便地进行 \(O(logn)\) 的区间修改与前缀查询。

方法：对 query 与 add 函数进行修改，使其返回二次前缀和结果。

数学分析如下：

\[\begin{aligned} \sum^r_{i=l}\sum^i_{j=l} t_j &=\sum^r_{i=l}(r-i+1)\times t_i\\ &=\sum^r_{i=l}((r+1)\times t_i-i\times t_i)\\ &=(r+1)\times\sum^r_{i=l}t_i-\sum^r_{i=l}i\times t_i \end{aligned} \]

所以，我们可以维护两个树状数组，其意义分别为 \(t_i\) 与 \(i\times t_i\) 的前缀。

代码如下：

int t1[maxn],t2[maxn];//t1为t的前缀,t2为i*t的前缀 
inline int lowbit(const int &x){return x&-x;}
void add(int pos,int val){
	int tem=pos;
	while(pos<=n) t1[pos]+=val,t2[pos]+=tem*val,pos+=lowbit(pos);
}
int query(int pos){
	int sum=0,tem=pos;
	while(pos) sum+=(tem+1)*t1[pos]-t2[pos],pos-=lowbit(pos);
	return sum;
}
void add_array(int l,int r,int val){add(l,val),add(r+1,-val);}
int query_array(int l,int r){return query(r)-query(l-1);}

简单包装为 class 可以有效增加代码的可读性。

inline int lowbit(const int &x){
	return x&-x;
}
class BIT{
	private:
		ll t[maxn];
	public:
		void add(int pos,ll val){
			for(int i=pos;i<=n;i+=lowbit(i)) t[i]+=val;
		}
		ll query(int pos){
			ll sum=0;
			for(int i=pos;i;i-=lowbit(i)) sum+=t[i];
			return sum;
		}
}

线段树

1 当不需要区间修改的线段树题目的做法

线段树是维护一个区间的树形结构。其维护的信息需要具有可加性（即通过组成大区间的两个小区间可以得到大区间的值）。

维护的信息具有可减性或其他可以使用树状数组的情况应用树状数组代替以获得更高的效率。

线段树的模板

struct node{
	int l,r;
	//other imformations
} t[4*maxn]; 
void pushup(node &u,node &l,node &r){
	//using l & r to make the new u
	//eg.
	//	u.val=l.val+r.val;
}
void build(int u,int l,int r){
	t[u]={l,r};
	if(l==r){
		// do something
	} else {
		int mid=l+r>>1;
		build(u<<1,l,mid),build(u<<1|1,mid+1,r);
		pushup(t[u],t[u<<1],t[u<<1|1]);
	}
}
void modify(int u,int pos,int val){
	if(t[u].l==t[u].r){
		// do modify
	} else {
		int mid=t[u].l+t[u].r>>1;
		if(pos<=mid) modity(u<<1,pos,val);
		else modify(u<<1|1,pos,val);
		pushup(t[u],t[u<<1],t[u<<1|1]);
	}
}
node query(int u,int l,int r){
	if(t[u].l>=l&&t[u].r<=r) return t[u];
	int mid=t[u].l+t[u].r>>1;
	if(r<=mid) return query(u<<1,l,r);
	else if(l>mid) return query(u<<1|1,l,r);
	node ans,ansl=query(u<<1,l,r),ansr=query(u<<1|1,l,r);
	pushup(ans,ansl,ansr);
	return ans;
}

此处 pushup 意为通过传入的后两个参数更新第一个位置的值，需要根据维护的具体信息修改。

build 的注释部分意为叶子结点的信息赋值，modify 的注释部分意为叶子结点的信息修改。这些部分均需要根据维护的信息改变。

有时维护的信息比较简单，query 可以不返回一整个结点，视题目而定。