PointNet论文学习

点云

基础知识

点云是指同一参考系下表达目标空间分布和目标表面特征的海量点集合，在获取物体表面每个采样点的空间坐标后，得到的是点的集合，这个就被我们称为点云。

点云的图像多为三维图像，即长度、宽度和深度信息。

点云的测量原理主要分为两种，一种是激光测量，一种则是摄影。激光测量得到的数据包括三维坐标和激光反射强度(强度信息与目标的表面材质、粗糙度、入射角方向及仪器发射能量等有关)，摄影得到的点云数据包括三维坐标（XYZ）和颜色信息（RGB）。当然，也可以两者进行结合，使用激光+摄影的方式，这样得到的点云数据包括三维坐标、激光反射强度和颜色信息。

点云图形的处理分为三个层次：

（1）低层次包括图像强化，滤波，关键点/边缘检测等基本操作

（2）中层次包括连通域标记，图像分割等操作

（3）高层次包括物体识别，场景分析等操作。工程中的任务需要用到多个层次的图像处理手段。

《PointNet: Deep Learning on Point Sets for 3D Classification and Segmentation》

名词解释

1、外在特征和内在特征

外在特征指的是观测角度不同，可能改变的信息，比如颜色，坐标，而内在特征则不随观测角度改变而转变，比如法线、曲率

2、局部特征和全局特征

局部特征主要是针对单个点及其领域的，比如法向量、局部形状等，更加注重局部的细节；全局特征关注点云整体的一些特性，例如几何中心、形状、大小等

公式解读

定理1：这里的h(xi)是将输入数据放置MLP中进行升维，以便提取更多的信息，MAX则是最大池化层，通过此函数提取特征，而后是γ，通过γ函数放入另一个MLP中，得到最终的分类结果或者分割结果，这个函数证明了PointNet的网络结构能拟合任何连续集合函数。

定理2：

（a）这里是说，对于任意的输入数据集S，都存在一个最小集Cs和最大集Ns，对于在Cs和Ns之间的任意集合T，其输出都与S一致，也就是说对于存在有噪声的数据和存在数据损坏的，都是有鲁棒性的。

（b）这里的Cs是最小集，也是关键点数，这里是说无论点数有多少，我们至多也只需要关注k个关键点，意味着即使丢失Ns-k个数据也不影响结果，保证鲁棒性，同时说明需要处理的关键参点也就k个，不会因为点数的增加而增加计算量

解决的主要问题

这篇解决了点云不规则无法直接读取的问题，他直接读取点云数据可以最大程度的减免精度损失，他解决的问题主要有以下几点：

点云的无序性

因为点云是一组没有顺序的点，所以我们这里需要做到即使顺序打乱，仍然不影响识别物体为同一物体，那么这里就需要我们引入一个是对称函数的网络，这里的PointNet采用了先个体，后整体的方式来处理点云

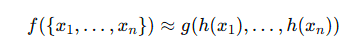
这里其实就是上面的公式解读的一部分，h(xi)函数用于个体特征提取，通过MLP对个体进行升维，而g()函数则是使用最大池化函数来处理所有点的特征，这个函数就是一个对称聚合的函数，无论顺序如何变化，最大值始终只有一个，这样就解决了无序的问题。

点云的相互关系

点云的这些点在一定的度量距离内，彼此之间并非孤立，因此我们需要考虑这个空间关系，而PointNet中采用的解决方案是将全局特征与局部特征进行串联，实现聚合信息，如下图所示：

这里的n*1088，其实就是局部特征n*64和全局特征n*1024拼接而来。

点云的旋转不变性

变换不变性，指的是点云作为一个几何目标，将它作为一个整体经过钢性变换（旋转、平移），其中的所有坐标（x,y,z）可能完全变化，但它仍然代表同一个物体，这里就需要我们去想如何实现模型能够始终识别同一物体，PointNet采用的方式是使用T-Net网络，它会将点云整体进行规范化，即将它调至一个规定的规范姿态，变化如下

变换后的点云 = 原始点云 × 变换矩阵
[N × K] = [N × K] × [K × K]

这样就只改变方向，而不改变大小，具体示例如下：

原始点云(侧翻90度) = [[0, 10, 1],   # 机头 (x=0, y=10, z=1)
           [0, 5, 3],    # 机身 (x=0, y=5, z=3)
           [-8, 5, 2]]   # 机翼 (x=-8, y=5, z=2)
旋转矩阵_A = [[1, 0, 0],
           [0, 0, -1],  
           [0, 1, 0]]  
对齐后的点云 = [[0, 1, -10],   # 机头：从(0,10,1)变为(0,1,-10)
              [0, 3, -5],    # 机身：从(0,5,3)变为(0,3,-5)
              [-8, 2, -5]]   # 机翼：从(-8,5,2)变为(-8,2,-5)

实际上，这个旋转矩阵不是固定不变的，它是根据点云来逐渐学习变化的，以此实现每次变化都能将点云调整至规定的规范姿态，它是如何实现的呢，接下来我们详细跟进代码

class STN3d(nn.Module):
    def __init__(self):
        super(STN3d, self).__init__()
        self.conv1 = torch.nn.Conv1d(3, 64, 1)
        self.conv2 = torch.nn.Conv1d(64, 128, 1)
        self.conv3 = torch.nn.Conv1d(128, 1024, 1)
        self.fc1 = nn.Linear(1024, 512)
        self.fc2 = nn.Linear(512, 256)
        self.fc3 = nn.Linear(256, 9)
        self.relu = nn.ReLU()

        self.bn1 = nn.BatchNorm1d(64)
        self.bn2 = nn.BatchNorm1d(128)
        self.bn3 = nn.BatchNorm1d(1024)
        self.bn4 = nn.BatchNorm1d(512)
        self.bn5 = nn.BatchNorm1d(256)


    def forward(self, x):
        batchsize = x.size()[0]
        x = F.relu(self.bn1(self.conv1(x)))
        x = F.relu(self.bn2(self.conv2(x)))
        x = F.relu(self.bn3(self.conv3(x)))
        x = torch.max(x, 2, keepdim=True)[0]
        x = x.view(-1, 1024)

        x = F.relu(self.bn4(self.fc1(x)))
        x = F.relu(self.bn5(self.fc2(x)))
        x = self.fc3(x)

        iden = Variable(torch.from_numpy(np.array([1,0,0,0,1,0,0,0,1]).astype(np.float32))).view(1,9).repeat(batchsize,1)
        if x.is_cuda:
            iden = iden.cuda()
        x = x + iden
        x = x.view(-1, 3, 3)
        return x

这里首先对函数进行卷积操作，从3维提升至64维，而后进行归一化，以防出现梯度爆炸和数据差异过大等情况，再使用激活函数Relu以实现非线性变化，后续也是类似，从64->128->1024，这里不直接直接从3->1024的原因是怕调整幅度过大出现梯度爆炸，而且逐步调整的参数更多(3*1024<3*64+64*128*1024)。此时升维完成，接下来是通过torch.max(x, 2, keepdim=True)[0]进行最大池化操作，此代码表示获取第二个维度的最大值，这里[0]是因为它有两个参数(值和索引)，此时就获取了每个特征通道最具代表性的响应值，接下来去除多余维度，本来是三个维度，即[batch_size,channels ,points]，我们现在只需要前两个即可，使用x = x.view(-1, 1024)自动调整，而后进行展平，再通过全连接层将参数降9个参数，再和展平后的单位矩阵进行相加，调整为3*3矩阵，就得到了空间变换矩阵。

同时这里加入了正则项约束变换矩阵接近正交：

L_reg = ||I - A @ A^T||_F^2

def feature_transform_regularizer(trans):
    d = trans.size()[1]#获取维度d
    batchsize = trans.size()[0]#获取批量大小
    I = torch.eye(d)[None, :, :]#扩展一个维度，且这个新维是第一个，由[d,d]-->[1,d,d]
    if trans.is_cuda:
        I = I.cuda()#使用GPU
    loss = torch.mean(torch.norm(torch.bmm(trans, trans.transpose(2,1)) - I, dim=(1,2)))#使用上面的公式来计算损失
    return loss##loss接近0说明是正交矩阵，那么就是正确的矩阵，因为正交矩阵不影响大小只改变方向，否则则再逐步优化

点云可能存在数据缺失

这里使用理论分析来保证模型鲁棒性，先解释下什么是鲁棒性，鲁棒性是指系统在面对不确定性、干扰、异常情况或输入变化时，仍能保持稳定性能和正常工作的能力。比如模型对输入数据噪声不敏感，数据缺失抵抗力强以及参数扰动及计算误差都有很好的稳定性，就可以说明其鲁棒性强。具体理论证明见上面公式解读（2）部分。

流程

主代码如下所示:（分析见注释）

class PointNetfeat(nn.Module):
    def __init__(self, global_feat = True, feature_transform = False):
        super(PointNetfeat, self).__init__()
        self.stn = STN3d()
        self.conv1 = torch.nn.Conv1d(3, 64, 1)
        self.conv2 = torch.nn.Conv1d(64, 128, 1)
        self.conv3 = torch.nn.Conv1d(128, 1024, 1)
        self.bn1 = nn.BatchNorm1d(64)
        self.bn2 = nn.BatchNorm1d(128)
        self.bn3 = nn.BatchNorm1d(1024)
        self.global_feat = global_feat
        self.feature_transform = feature_transform
        if self.feature_transform:
            self.fstn = STNkd(k=64)

    def forward(self, x):
        n_pts = x.size()[2]#x=[批量大小,维度，点数]获取点数N
        trans = self.stn(x)#获取空间变换矩阵，结构3*3
        x = x.transpose(2, 1)#转换张量格式，由[B,3,N]-->[B,N,3],以便和空间变换矩阵做乘法
        x = torch.bmm(x, trans)#进行矩阵相乘以转换为标准姿态
        x = x.transpose(2, 1)#从[B,N,3]-->[B,3,N]
        x = F.relu(self.bn1(self.conv1(x)))#先做卷积操作，嵌套标准化，再使用激活函数进行操作

        if self.feature_transform:#是否使用特征空间变换
            trans_feat = self.fstn(x)#同之前一样，变换维度乘上空间变换矩阵，不过这里是64*64的维度
            x = x.transpose(2,1)
            x = torch.bmm(x, trans_feat)
            x = x.transpose(2,1)
        else:
            trans_feat = None

        pointfeat = x #保留[批量大小，维度，点数]局部特征，用于后续分割任务
        x = F.relu(self.bn2(self.conv2(x)))#64->128
        x = self.bn3(self.conv3(x))#128->1024
        x = torch.max(x, 2, keepdim=True)[0]#最大池化提取特征，[B,1024,N]-->[B,1024,1]
        x = x.view(-1, 1024)#三维变二维，取消多余维度
        if self.global_feat:#如果是分类任务，应用全局特征
            return x, trans, trans_feat
        else:#分割任务，局部+全局特征
            x = x.view(-1, 1024, 1).repeat(1, 1, n_pts)#[B,1024]-->[B,1024,N]，将全局特征复制到每个点
            return torch.cat([x, pointfeat], 1), trans, trans_feat#拼接，[B,1024,N]-->[B,1088,N]

以上主要是获取特征的代码，Pointnet主要有两个任务，分类和分割任务，首先看分类任务

class PointNetCls(nn.Module):#分类任务
    def __init__(self, k=2, feature_transform=False):
        super(PointNetCls, self).__init__()
        self.feature_transform = feature_transform
        self.feat = PointNetfeat(global_feat=True, feature_transform=feature_transform)
        self.fc1 = nn.Linear(1024, 512)
        self.fc2 = nn.Linear(512, 256)
        self.fc3 = nn.Linear(256, k)
        self.dropout = nn.Dropout(p=0.3)
        self.bn1 = nn.BatchNorm1d(512)
        self.bn2 = nn.BatchNorm1d(256)
        self.relu = nn.ReLU()

    def forward(self, x):
        x, trans, trans_feat = self.feat(x)#特征提取，其中x=[B,1024]，trans=[B,3,3],trans_feat=[B,64,64]（如果存在）
        x = F.relu(self.bn1(self.fc1(x)))#经过全连接层，从1024->512
        x = F.relu(self.bn2(self.dropout(self.fc2(x))))#第二个全连接层，512->256,带有dropout，以防过拟合情况出现
        x = self.fc3(x)#第三个全连接层，256->k
        return F.log_softmax(x, dim=1), trans, trans_feat#返回类别概率

分割任务如下

class PointNetDenseCls(nn.Module):#分割任务
    def __init__(self, k = 2, feature_transform=False):
        super(PointNetDenseCls, self).__init__()
        self.k = k #分割类别数
        self.feature_transform=feature_transform
        self.feat = PointNetfeat(global_feat=False, feature_transform=feature_transform)
        self.conv1 = torch.nn.Conv1d(1088, 512, 1)
        self.conv2 = torch.nn.Conv1d(512, 256, 1)
        self.conv3 = torch.nn.Conv1d(256, 128, 1)
        self.conv4 = torch.nn.Conv1d(128, self.k, 1)
        self.bn1 = nn.BatchNorm1d(512)
        self.bn2 = nn.BatchNorm1d(256)
        self.bn3 = nn.BatchNorm1d(128)

    def forward(self, x):
        batchsize = x.size()[0]#获取批量大小B
        n_pts = x.size()[2]#获取点数N
        x, trans, trans_feat = self.feat(x)#获取特征和空间变换矩阵
        x = F.relu(self.bn1(self.conv1(x)))#[B,1088,N]-->[B,512,N]
        x = F.relu(self.bn2(self.conv2(x)))#[B,512,N]-->[B,256,N]
        x = F.relu(self.bn3(self.conv3(x)))#[B,256,N]-->[B,128,N]
        x = self.conv4(x)#[B,128,N]-->[B,k,N]
        x = x.transpose(2,1).contiguous()## [B, k, N] --> [B, N, k]
        x = F.log_softmax(x.view(-1,self.k), dim=-1)#计算类别概率
        x = x.view(batchsize, n_pts, self.k)#重塑维度为[B,N,K]
        return x, trans, trans_feat

这里解释一下可能存在疑问的地方：为什么64维是局部特征，而1024是全局特征?

局部特征的特点是MLP对每个点单独处理，每个点只知道自己的坐标而不知道其他的信息，反观全局特征，他的特点是基于整个点云的所有点，包含了所有点的统计信息。在具体看这里，64维时是MLP对每个点单独进行升维，而1024维则是进行了最大池化操作，它汇聚了所有点的最大值，包含了整个点云的信息，所以它是全局特征。

复现

需要注意的点是官网的数据集已不可访问，下载时需要找到非normal版本的，否则与此代码是不适配的，同时此代码原来是在linux系统下跑的，所以中间有用到so文件，具体是render_balls_so.so这个文件，show_seg.py用到了show3d_balls.py里面的showpoints函数，show3d_balls.py用到了一个它，需要我们使用Visual Studio来转换为dll文件

分类任务

分类任务训练，在参数里给定具体的值，然后直接运行文件即可

parser.add_argument('--dataset', type=str, default="../dataset/shapenetcore_partanno_segmentation_benchmark_v0", help="dataset path")
parser.add_argument('--dataset_type', type=str, default='shapenet', help="dataset type shapenet|modelnet40")
parser.add_argument(
    '--nepoch', type=int, default=5, help='number of epochs to train for')

训练结果如下图

接下来就可以进行测试了，再运行show_cls文件即可查看结果

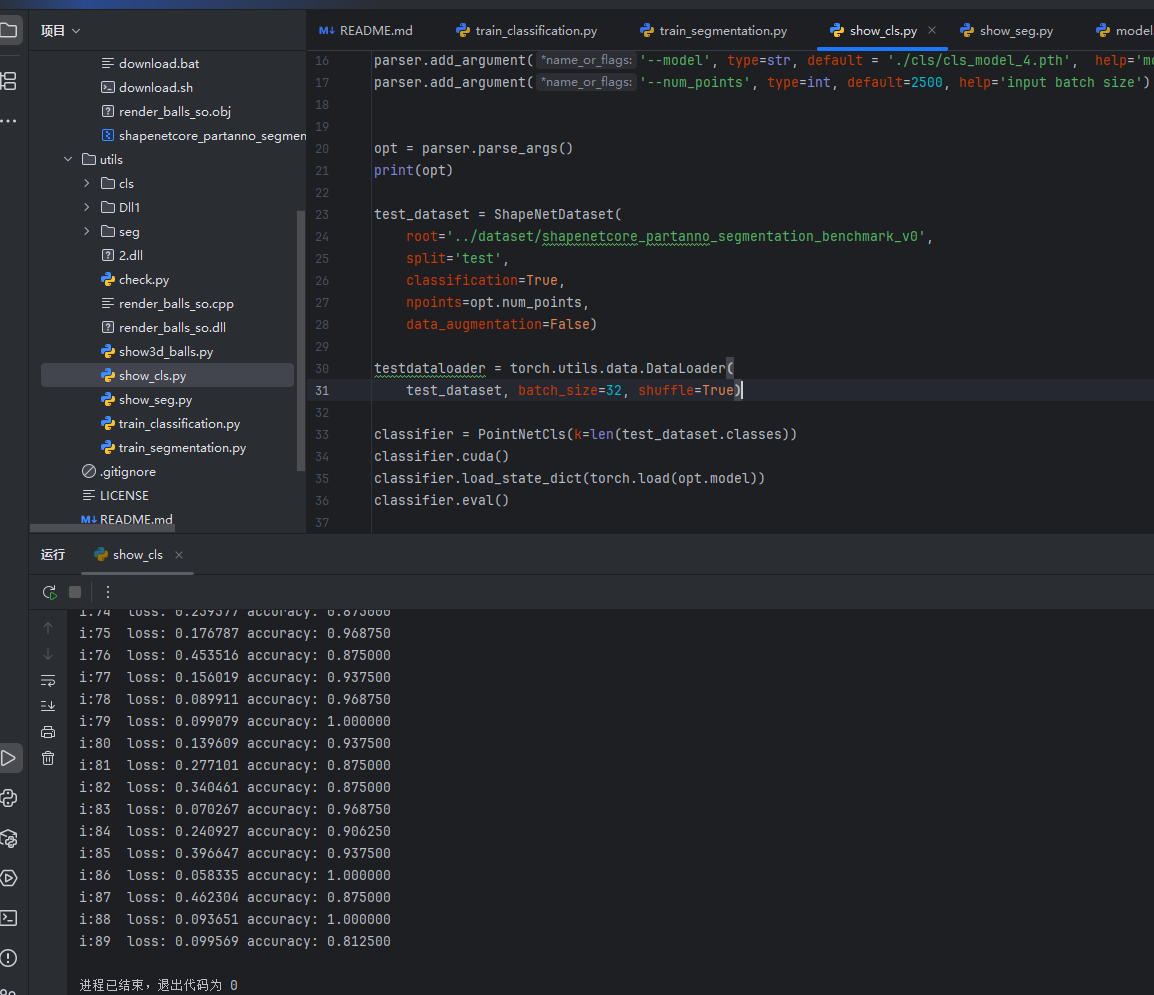
分割任务

这里需要指定一下分割的物体，在参数里设定即可，这里以飞机为例

parser = argparse.ArgumentParser()
parser.add_argument(
    '--batchSize', type=int, default=16, help='input batch size')
parser.add_argument(
    '--workers', type=int, help='number of data loading workers', default=0)
parser.add_argument(
    '--nepoch', type=int, default=25, help='number of epochs to train for')
parser.add_argument('--outf', type=str, default='seg', help='output folder')
parser.add_argument('--model', type=str, default='', help='model path')
parser.add_argument('--dataset', type=str, default="../dataset/shapenetcore_partanno_segmentation_benchmark_v0", help="dataset path")
parser.add_argument('--class_choice', type=str, default='Chair', help="class_choice")
parser.add_argument('--feature_transform', action='store_true', help="use feature transform")