海报PLA （HYSBZ - 1113）单调栈模板

测评：https://www.luogu.com.cn/problem/P3467

N个矩形,排成一排. 现在希望用尽量少的矩形海报Cover住它们.

Input

第一行给出数字N,代表有N个矩形.N在[1,250000] 下面N行,每行给出矩形的长与宽.其值在[1,1000000000]2 1/2 Postering

Output

最少数量的海报数.

 

Sample Input

5

1 2

1 3

2 2

2 5

1 4 

Sample Output

4

                             

 

---

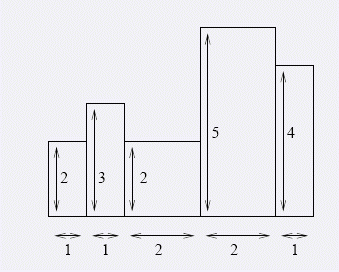
先解释下题意，题目说的不是很清楚

看上面两幅图，是样例的排列方式，其中可以发现有一个隐藏条件，空白不能被覆盖（我刚开始看到题目以为一大张糊上去就可以了……）

 

先考虑最简单的情况：

当遇到一低一高时，必须要用两张，但如果后面又遇到一个和第一张高度相等的，三个矩形，两张就覆盖了----省了一张

但如果一高一低，后面第三个矩形无论是高是低都省不了。

 

所以想「节省」海报，只有：「低高低」，或着「低高低低」，或者「低低高低」 等等这类情况。

最坏情况，每个矩形需要一张独立的海报，也就是 n 张。

我们需要做的是：统计出可以「节省」几张海报，有几个矩形不必花费一张独立的海报？

 

因此：

我们维护一个单调递增的单调栈，宽度不管，就看高度。

只要递增，元素就依次入栈；

如果递减，那就弹出栈顶元素，直到确保严格递增。

在出栈过程中，需要注意特判一个条件：如果栈顶元素与入栈元素相等，那么就能省一张，cnt ++。

最终答案就是 n - cnt。

 

代码如下：

#include<stdio.h>
#include<algorithm>
using namespace std;
int a[250001],stk[250001],top,n,k;

int main()
{
    scanf("%d",&n);
    for(int i=1;i<=n;++i)
    {
        int d,h;
        scanf("%d%d",&d,&h);
        while(top>0 && h<=stk[top]){
            if(h==stk[top]) k++;
            top--;
        }
        stk[++top]=h;
    }
    printf("%d",n-k);
    return 0;
}