卷积网络基本原理

一、人工神经网络处理图像分类问题缺点

1、权值太多，参数爆炸

2、语义上理解存在问题，全连接网络对待相邻、距离很远的像素都是无差别的对待，不考虑图像内容的空间结构

 

还拿最常用的例子，猫识别。假如我输入一张64 64的图片，由于有三个颜色通道，所以输入的向量是一个64 64 3=12288维的列向量。这其实还不算大，但我们一般处理的图片可比这个大的多。

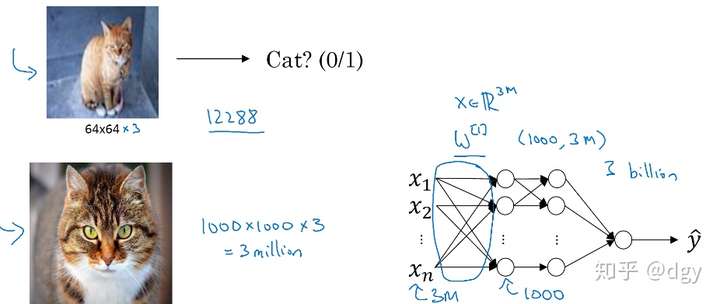
好比说输入是一个1000 1000的图片。那么输入向量的维度经过计算可得1000 1000 3=3M，假设第一层有1000个神经元，那么权值矩阵 的维度将是1000 3M，即有30亿个数据。参数如此庞大，意味着难以获得足够数据防止神经网络发生过拟合和竞争需求，同时，巨大的内存需求也让人难以承受。

 

卷积操作充分利用了图片相邻区域的信息，通过稀疏连接与共享权值的方式大大减少参数矩阵的规模，从而减少计算量，也大大的提高了收敛速度。

二、卷积网络的基本概念

通过上面的例子，我们可以发现，之所以普通的神经网络不能用，问题就出在权值矩阵W身上，W太大，参数过多，训练起来太吃力。于是，我们便想到，我们能不能不用W？这样不就避免数据过多了么？我们可以直接不用 这一线性运算，而找一个其他的运算方法来避免使用W。我们找到的其他运算方法便是卷积运算。

我们之前在说面部识别介绍过，要识别面部，都是从细微的边缘入手，一层一层聚类，最终实现人脸的识别。我们就以边缘检测为例子，介绍卷积运算。

假设输入一张灰度图像，由于是灰度图像，所以不存在三个颜色通道。我们要检测出这个图像中的垂直边缘，就像下图的栏杆这样的竖直边缘，那我们应该怎么做呢？

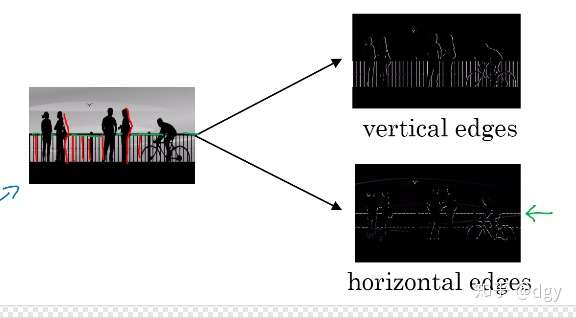
这时我们便要用一个专门筛选竖直边缘的过滤器将所有的垂直边缘过滤出来。具体的操作是这样的，将这个图片不要展开成向量，而是保持矩阵形态，直接与一个过滤器进行卷积运算。如果是垂直边缘检测，那我们一般用的过滤器是这样的：

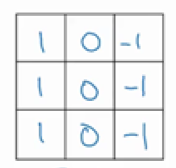
假设灰度图像矩阵如下

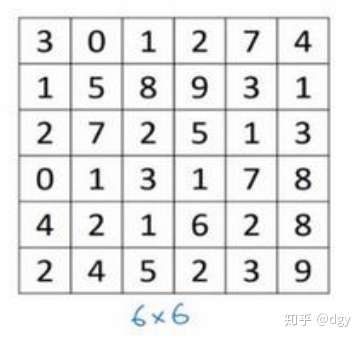
两者做卷积，首先将过滤器重叠在图像的左上角

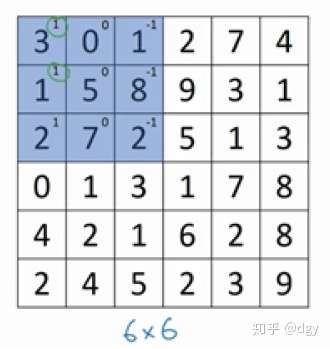
将重叠的数字对应相乘再求和便得到第一行第一列数据，即 ，将过滤器向右平移一格，就得到第一行第二列的数据；将过滤器向下平移一格，就得到第二行第一列的数据，依次类推。于是这个图像经边缘过滤器卷积之后的矩阵如下：

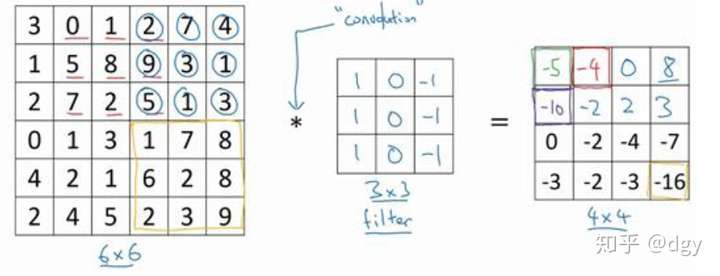
这里最终得到的是一个4维的矩阵，应用数学知识不难得出，如果输入矩阵为n维，过滤器为f维，那么输出矩阵为n-f+1维。

我们来说一下，为什么这个过滤器可以筛选出垂直边缘。我们输入一个左右灰度不同图像：

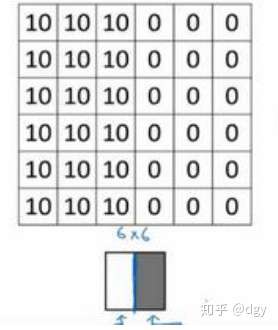
我们可以清楚的看到在左右的交界处有一个垂直边缘。我们把这个图与之前的过滤器进行卷积运算：

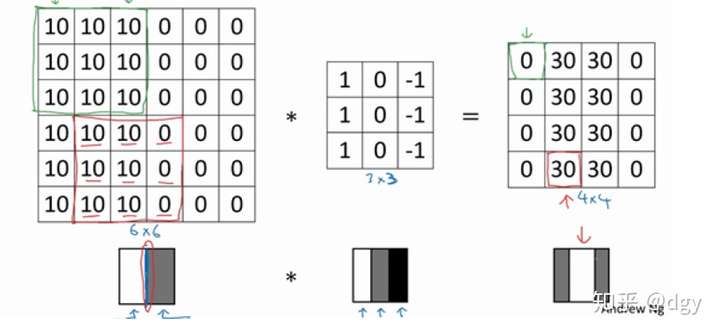
我们可以看到，输出图像把交界处的边缘识别为中间高灰度区域，所以说我们应用的过滤器，一旦在图片中碰到这种垂直的边缘，便可以很好的识别出来。这种过滤器不仅可以将边缘识别出来，同时识别这个边缘是由亮到暗还是由暗到亮，同样这个过滤器，如果把图片左右翻转，我们来看一下识别的结果：

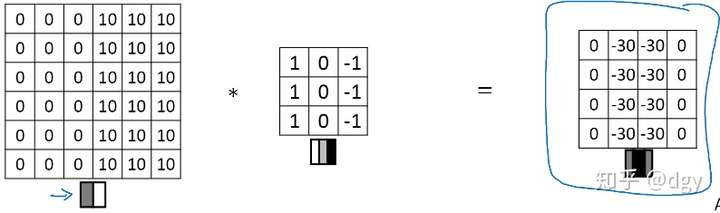
我们可以看到，识别出来的边缘变成一个负灰度区域，也就是输入的图片含有一个负垂直边缘。这是垂直边缘，那水平边缘呢？我们很容易想到将过滤器旋转就可以得到水平边缘过滤器：

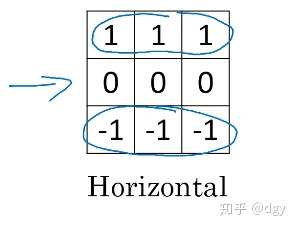
我们来看一个稍稍复杂的例子，输入图像如下：

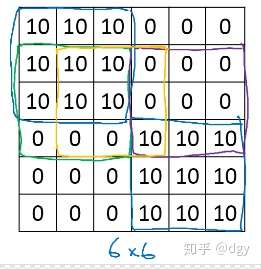
实际上它是这样的：

我们可以看到它有两个水平边缘，左边的是一个正边缘，即由亮到暗；右边则是一个负边缘，即由暗到亮，我们把它与水平边缘过滤器进行卷积运算：

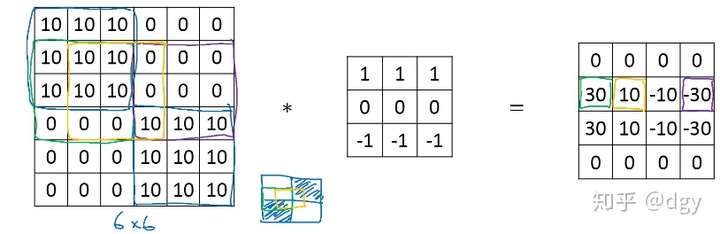
我们可以看到，识别结果左边为正灰度，右边为负灰度，与我们之前肉眼识别的结果相符合。

我们介绍了两种过滤器，但过滤器其实就是一个矩阵，里面的数字组合千变万化，对应实现的过滤功能也各不相同，即使同种功能也可以有多种过滤器，过滤效果各有千秋。就拿垂直边缘过滤器来说，除了上面介绍的，还有一种：

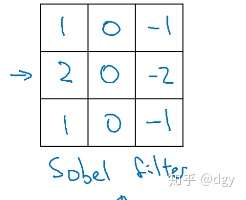
这叫sobel过滤器，它增加了中间一行的权重，使得结果的鲁棒性更强。还可以将权重再提高一些，这种叫做scharr过滤器：

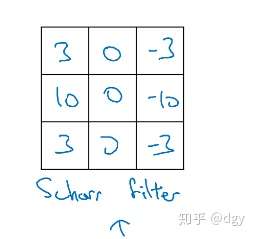
总之，不同过滤器实现不同功能，同样的，你也可以利用梯度下降法训练你自己的过滤器，你要实现某种功能，就把过滤器里面的数字当成参数一样训练，这样最终可以找到实现特定功能的过滤器。

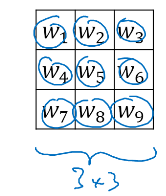
1、卷积滤波

对于一张二维图片和一个二维的卷积核滤波矩阵K卷及操作可以表示：

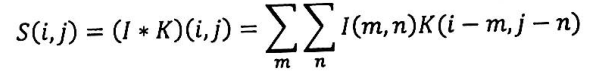
卷积过程：

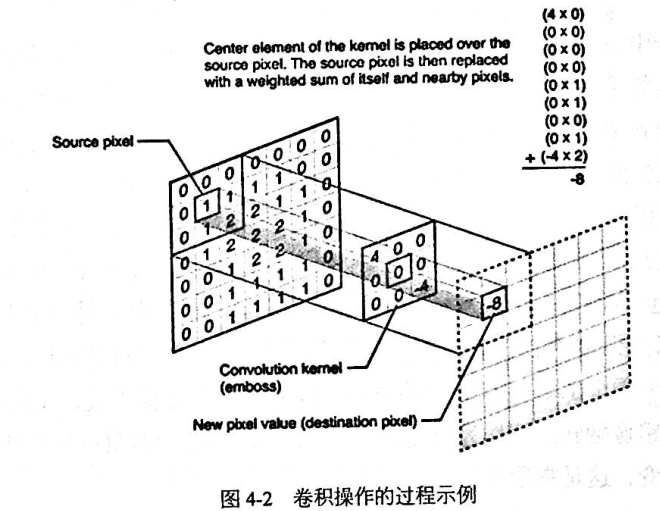
简单说，对于图片每一个像素点，计算它的邻域像素和滤波器矩阵的对应位置元素的乘积然后将所有乘积累积加，作为该像素位置的输出值。卷积核依次滑过图片中每一个像素位置，就可以输出分辨率不变的新图片。

卷积核实际上就是一个权值矩阵，表示如何处理单个像素与其邻域像素之间的关系。卷积核矩阵的尺寸与计算量成正比，尺寸越大计算量越大。卷积核矩阵内的元素不仅影响输出效果，还影响输出图片的亮度，元素累加和S,等于1，亮度不变，S>1，变亮，S<1，变暗，S=0，亮度非常低，用于提取边缘。卷积操作对于边缘提取有两种方式：1.“Valid padding"直接忽略无法计算的边缘，输出图片尺寸变小，“SAME padding”对外围进行0填充使边缘合法计算，尺寸不变。

 

2、卷积层

每一个卷积核都会生成一幅新的图像，在卷积网络中，生成的图像叫做特征图，可以理解为图片经过滤波后的不同通道。

特点：1、局部感知域   2、权值共享   3、多核卷积

 1）、局部感知域

对于每一个计算单元来说，只考虑其像素位置附近的输入，并不需要与上一层的所有节点相连。

在之前看到的全连接层的网络中,输入被描绘成纵向排列的神经元。但在一个卷积网络中,把输入看作是一个 28 × 28 的方形排列的神经元更有帮助,其值对应于我们用作输入 28 × 28 的像素光强度:

第一个隐藏层中的每个神经元会连接到一个输入神经元的一个小区域,例如,一个 5 × 5 的区域,对应于 25 个输入像素。所以对于一个特定的隐藏神经元,可能有看起来像这样的连接:

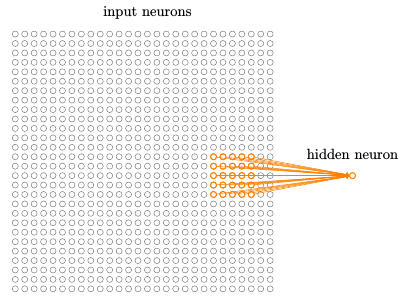
每个连接学习一个权重。而隐藏神经元同时也学习一个总的偏置。

然后在整个输入图像上交叉移动局部感受野。对于每个局部感受野,在第一个隐藏层中有一个不同的隐藏神经元。

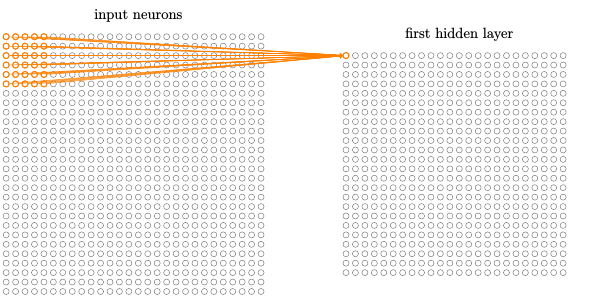
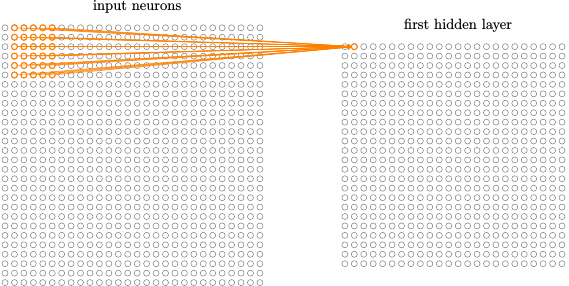
注意如果有一个 28 × 28 的输入图像,5 × 5 的局部感受野,那么隐藏层中就会有 24 × 24 个神经元。实际上,有时候会使用不同的跨距。例如,可以往右(或下)移动 2 个像素的局部感受野,这种情况下我们使用了 2 个跨距。

 2）、权值共享

对一张图片进行卷积的时候，会让卷积逐一滑动图片的每一个像素，也就是说，处理每一个像素点的参数都相同。

每个隐藏神经元具有一个偏置和连接到它的局部感受野的5 × 5 权重。对 24 × 24 隐藏神经元中的每一个使用相同的权重和偏置。

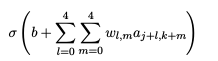
这意味着第一个隐藏层的所有神经元检测完全相同的特征 3 ,只是在输入图像的不同位置。要明白为什么是这个道理,把权重和偏置设想成隐藏神经元可以挑选的东西,例如,在一个特定的局部感受野的垂直边缘。这种能力在图像的其它位置也很可能是有用的。因此,在图像中应用相同的特征检测器是非常有用的。用稍微更抽象的术语,卷积网络能很好地适应图像的平移不变性:例如稍稍移动一幅猫的图像,它仍然是一幅猫的图像。因为这个原因,有时候把从输入层到隐藏层的映射称为一个特征映射。把定义特征映射的权重称为共享权重。把以这种方式定义特征映射的偏置称为共享偏置。共享权重和偏置经常被称为一个卷积核或者滤波器。

目前描述的网络结构只能检测一种局部特征的类型。为了完成图像识别需要超过一个的特征映射。所以一个完整的卷积层由几个不同的特征映射组成:

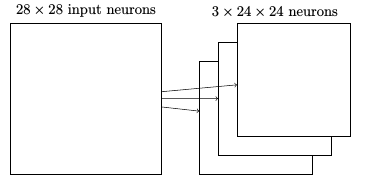
在这个例子中,有 3 个特征映射。每个特征映射定义为一个 5 × 5 共享权重和单个共享偏置的集合。其结果是网络能够检测 3 种不同的特征,每个特征都在整个图像中可检测。一种早期的识别 MNIST 数字的卷积网络,LeNet-5,使用 6 个特征映射,每个关联到一个 5 × 5 的局部感受野。所以上面的插图例子实际和 LeNet-5 很接近。

下面看一个20卷积核（20个特征映射）的例子：

这 20 幅图像对应于 20 个不同的特征映射(或滤波器、核)。每个映射有一幅 5 × 5 块的图像表示,对应于局部感受野中的 5 × 5 权重。白色块意味着一个小(典型的,更小的负数)权重,所以这样的特征映射对相应的输入像素有更小的响应。更暗的块意味着一个更大的权重,所以这样的特征映射对相应的输入像素有更大的响应。

所以我们能从这些特征映射中得到什么结论?很明显这里有超出了我们期望的空间结构:这些特征许多有清晰的亮和暗的子区域。这表示我们的网络实际上正在学习和空间结构相关的东西。

共享权重和偏置的一个很大的优点是,它大大减少了参与的卷积网络的参数。对于每个特征映射我们需要 25 = 5 × 5 个共享权重,加上一个共享偏置。所以每个特征映射需要 26 个参数。如果我们有 20 个特征映射,那么总共有 20 × 26 = 520 个参数来定义卷积层。作为对比,假设我们有一个全连接的第一层,具有 784 = 28 × 28 个输入神经元,和一个相对适中的 30 个隐藏神经元,正如我们在本书之前的很多例子中使用的。总共有 784 × 30 个权重,加上额外的 30 个偏置,共有 23, 550 个参数。换句话说,这个全连接的层有多达 40 倍于卷基层的参数。

3）、多核卷积

每个卷积核是一个特征提取器，所以使用多个卷积核，充分提取特征。

 

 

 

3、池化层（降维）: 除了刚刚描述的卷积层,卷积神经网络也包含池化层(pooling layers)。池化层通常紧接着在卷积层之后使用。它要做的是简化从卷积层输出的信息，使特征具有“平移不变性”。

一个池化层取得从卷积层输出的每一个特征 ，并且从它们准备一个凝缩的特征映射。作为一个具体的例子,常用的混合的程序被称为最大值池化(max-pooling)，均值池化（average-pool）。

 

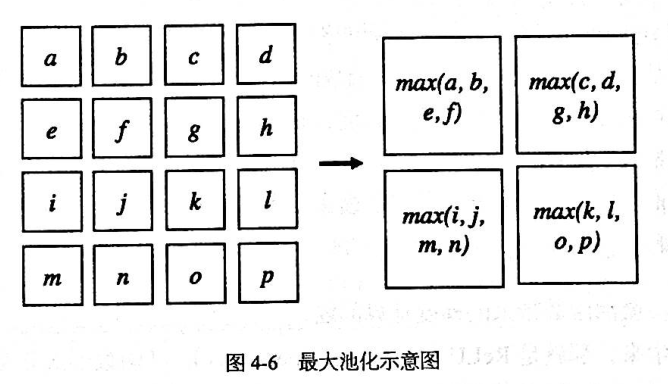
从卷积层有 24 × 24 个神经元输出,池化后我们得到 12 × 12 个神经元。

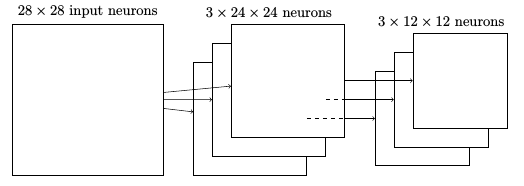
另一个常用的方法是 L2 混合(L2 pooling)。这里我们取 2 × 2 区域中激活值的平方和的平方根,而不是最大激活值。

综合在一起: 我们现在可以把这些思想都放在一起来构建一个完整的卷积神经网络。它和我们刚看到的架构相似,但是有额外的一层 10 个输出神经元,对应于 10 个可能的 MNIST 数字(’0’,’1’,’2’ 等):

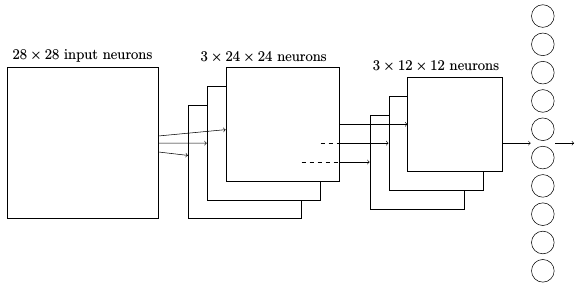
这个网络从 28 × 28 个输入神经元开始,这些神经元用于对 MNIST 图像的像素强度进行编码。接着的是一个卷积层,使用一个 5 × 5 局部感受野和 3 个特征映射。其结果是一个 3 × 24 × 24隐藏特征神经元层。下一步是一个最大值混合层,应用于 2 × 2 区域,遍及 3 个特征映射。结果是一个 3 × 12 × 12 隐藏特征神经元层。网络中最后连接的层是一个全连接层。更确切地说,这一层将最大值混合层的每一个神经元连接到每一个输出神经元。

 

4、激活函数

去线性化

tf.nn.relu()

5、多层卷积