树
一、完全二叉树
若设二叉树的深度为k,除第 k 层外,其它各层 (1~k-1) 的结点数都达到最大个数,第k 层所有的结点都连续集中在最左边,这就是完全二叉树。
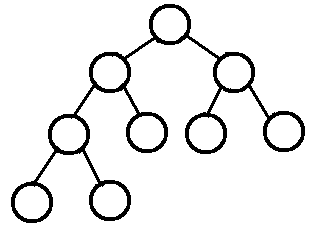
二、二叉搜索树-BST
对于二叉搜索树,对于每一个节点,其左节点值比当前节点值小,右节点值比当前节点值大。
三、平衡二叉树-AVL树
1. 它或者是一颗空树,或它的左子树和右子树的深度之差(平衡因子)的绝对值不超过1,且它的左子树和右子树都是一颗平衡二叉树。
2. 平衡二叉树也是一个二叉搜索树。
四、B树
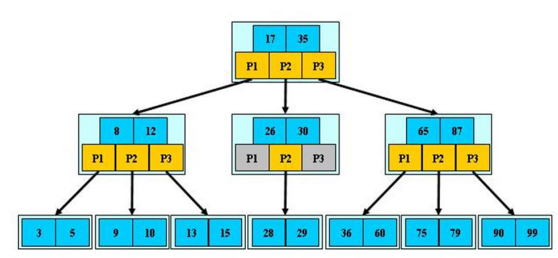
特性:
- B树的阶m:节点的最多子结点个数。
-
根结点至少拥有两颗子树(存在子树的情况下),根结点至少有一个关键字;
-
除了根结点以外,其余每个分支结点至少拥有 m/2 棵子树;
-
所有的叶结点都在同一层上,B树的叶子结点可以看成是一种外部节点,不包含任何信息;
-
有 k 棵子树的分支结点则存在 k-1 个关键码,关键码按照递增次序进行排列;
-
关键字数量需要满足ceil(m/2)-1 <= n <= m-1;
优点:
总的来说就是利用平衡树的优势,保证了查询的稳定性和加快了查询的速度。
五、B+树
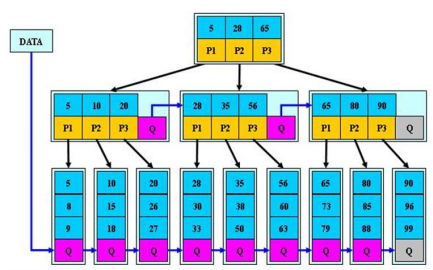
-
查询不同;B树在找到具体的数值以后就结束,而B+树则需要通过索引找到叶子结点中的数据才结束,也就是说B+树的搜索过程中走了一条从根结点到叶子结点的路径,其高度是相同的,相对来说更加的稳定;
-
区间访问:B+树的叶子结点会按照顺序建立起链状指针,可以进行区间访问;
- 存储的位置不同;B+树中的数据都存储在叶子结点上,也就是其所有叶子结点的数据组合起来就是完整的数据,但是B树的数据存储在每一个结点中,并不仅仅存储在叶子结点上。
为什么数据库索引使用B+树而不是B树?
- B+树的磁盘读写代价更低:B+树的内部节点并没有指向关键字具体信息的指针,因此其内部节点相对B树更小,如果把所有同一内部节点的关键字存放在同一盘块中,那么盘块所能容纳的关键字数量也越多,一次性读入内存的需要查找的关键字也就越多,相对IO读写次数就降低了。
- B+树的查询效率更加稳定:由于非终结点并不是最终指向文件内容的结点,而只是叶子结点中关键字的索引。所以任何关键字的查找必须走一条从根结点到叶子结点的路。所有关键字查询的路径长度相同,导致每一个数据的查询效率相当。
- 区间查询:B+树的叶子结点会按照顺序建立起链状指针,可以进行区间访问;
六、红黑树
红黑树是一种含有红黑结点并能自平衡的二叉查找树。它必须满足下面性质:
- 每个节点要么是黑色,要么是红色。
- 根节点是黑色。
- 每个叶子节点(NIL)是黑色。
- 每个红色结点的两个子结点一定都是黑色。
- 任意一结点到每个叶子结点的路径都包含数量相同的黑结点。
- 红黑树相对平衡,从而保证了红黑树的查找、插入、删除的时间复杂度最坏为O(log n)。加快检索速率。
- 红黑树相比avl树,在检索的时候效率其实差不多,都是通过平衡来二分查找。但对于插入删除等操作效率提高很多。
为什么数据库索引使用B+树而不是红黑?
- B+树是多叉树,相同数据情况下B+树层数更少,查询效率高。磁盘读写代价更低。
-
磁盘预读特性:为了减少磁盘 I/O 操作,磁盘往往不是严格按需读取,而是每次都会预读。预读过程中,磁盘进行顺序读取,顺序读取不需要进行磁盘寻道,并且只需要很短的磁盘旋转时间,速度会非常快。并且可以利用预读特性,相邻的节点也能够被预先载入。
七、字典树(前缀树)_Java实现
1 class TrieNode{ 2 TrieNode[] child; 3 boolean is_end; 4 TrieNode(){ 5 child = new TrieNode[26]; 6 is_end = false; 7 } 8 } 9 class Trie { 10 TrieNode root; 11 /** Initialize your data structure here. */ 12 public Trie() { 13 root = new TrieNode(); 14 } 15 16 /** Inserts a word into the trie. */ 17 public void insert(String word) { 18 TrieNode node = root; 19 for(int i=0;i<word.length();i++){ 20 char c = word.charAt(i); 21 if(node.child[c-'a'] == null){ 22 node.child[c-'a'] = new TrieNode(); 23 } 24 node = node.child[c-'a']; 25 } 26 node.is_end = true; 27 } 28 29 /** Returns if the word is in the trie. */ 30 public boolean search(String word) { 31 TrieNode node = root; 32 for(int i=0;i<word.length();i++){ 33 char c = word.charAt(i); 34 if(node.child[c-'a'] == null){ 35 return false; 36 } 37 node = node.child[c-'a']; 38 } 39 return node.is_end; 40 } 41 42 43 public boolean startsWith(String prefix) { 44 TrieNode node = root; 45 for(int i=0;i<prefix.length();i++){ 46 char c = prefix.charAt(i); 47 if(node.child[c-'a'] == null){ 48 return false; 49 } 50 node = node.child[c-'a']; 51 } 52 return true; 53 } 54 }



 浙公网安备 33010602011771号
浙公网安备 33010602011771号