字符串 - AC 自动机

这里有一些别样的学习思路。

KMP

用途

单模式串匹配。

过程

我们分解 \(O(nm)\) 的算法过程。

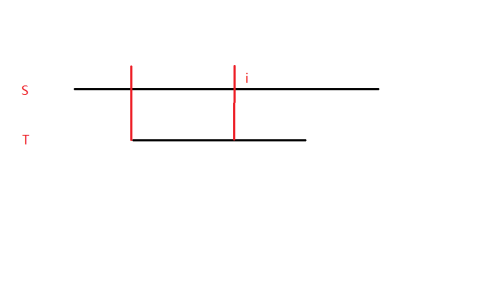
如图，红色竖线包括的为目前匹配成功的部分，对于下一位 \(i\) ：

首先，如果成功匹配，那么匹配长度加一。

否则，我们考虑失配情况。

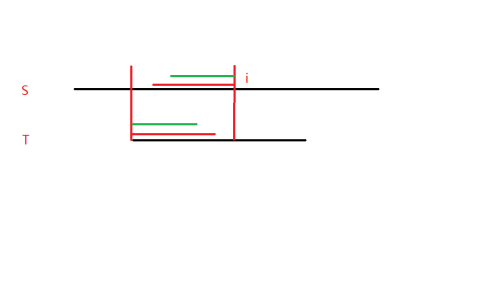
我们会将 \(S\) 串的匹配部分左端点向右移动一位，然后 \(T\) 串从头匹配。

我们发现，如果想要再次考虑第 \(i\) 位，最起码需要匹配到如上图中红色横线的部分，也就是说红色横线的部分完全相等。

如果不完全相等，我们需要比较绿色横线的部分，如此以往。

要么，我们找到了另一个起点，使得我们可以重新考虑第 \(i\) 位的匹配情况。
要么，我们遍历了所有的起点，不存在这种情况，即第 \(i\) 位前不存在可以拼接上 \(i\) 的后缀，我们就以第 \(i\) 位为起点开始重复这个过程。

可以发现，第一种情况中，我们一定找到了红色竖线内的 \(T\) 串 的 最长公共前后缀。

也就是说，当失配时，我们只需要知道，当前已匹配 \(T\) 串部分（一定是 \(T\) 的前缀）的最长公共前后缀。
如果仍然失配，我们继续找到 \(T\) 的最长公共前后缀的最长公共前后缀，重复此过程。

• 一个字符串 \(S\) 的 最长公共前后缀 为 \(S\) 的长度最长的真子串 \(T\)，满足 \(T\) 既是 \(S\) 的前缀，也是 \(S\) 的后缀，以下称作 \(\texttt{boarder}\)。

由此，我们便建立了较为完整的思维过程来优化此算法。

可以发现，我们尽可能地减少了重复的，或者说无意义的比较，算法的 正确性 由此保证。

\(\texttt{boarder}\) 求法

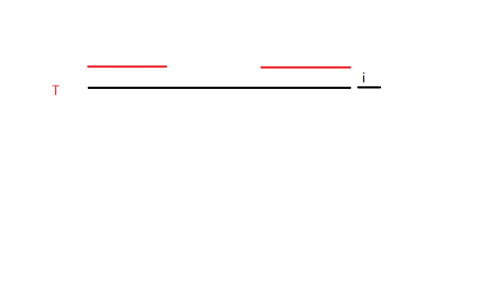
我们用红色横线表示第 \(i - 1\) 位的 \(\texttt{boarder}\)。
可以发现，此过程类似于 \(T\) 的自身匹配，与上述优化过程类似。
请读者自行推导本过程。

时间复杂度

首先来看两主要部分代码：

for (int i = 2, j = 0; i <= M; ++i) {
	while (j and t[j + 1] != t[i]) j = p[j];
	if (t[j + 1] == t[i]) ++j;
	p[i] = j;
}
for (int i = 1, j = 0; i <= N; ++i) {
	while (j and s[i] != t[j + 1]) j = p[j];
	if (s[i] == t[j + 1]) ++j;
	if (j == M) ans.push_back(i - M + 1), j = p[j];
}
//Luogu P3375

以 \(\texttt{boarder}\) 的处理为例，我们发现，变量 \(j\) 最多增量为 \(O(n)\)，也就最多向前 跳 \(O(n)\) 次，复杂度为 \(O(n)\)。
匹配过程同理。

如果 \(\left| S \right| = n, \left| T \right| = m\)
则总时间复杂度 \(O(n + m)\)。

AC 自动机

用途

多模式串匹配。

引入

我们考虑暴力方式，因为是多模式串，我们需要对模式串建一棵 \(Tire\) 树。
（\(Tire\) 树不在此处涉及，已默认各位学过 \(Tire\) 树）

然后对于匹配串，我们对于它的每一个前缀 \(T\)，\(S\) 为 \(Tire\) 树上存在的 \(T\) 的最长后缀。
\(Tire\) 树上代表 \(S\) 的结点到根路径上的所有尾结点答案加一。

这是我们的暴力思路。

可以发现，制约复杂度的最大因素是找 \(S\) 串的过程，我们尝试优化这个过程。

增量，当前处理完的前缀为 \(T'\)，得到的最长后缀为 \(S\)，下一位考虑的字符为 \(c\)。
如果 \(S\) 拼接上 \(c\) 后仍然可以在 \(Trie\) 树上找到，直接继承。
否则，我们需要找到 \(S\) 在 \(Tire\) 树上存在的每一个后缀，
（因为只有后缀在 \(Trie\) 树上存在，再拼接一个字符才可能在 \(Trie\) 树上）
可以发现这和之前的 \(KMP\) 算法过程类似。

为了加快这个进程，我们需要和 \(KMP\) 的 \(\texttt{boarder}\) 类似的东西， \(\texttt{Fail}\) 指针。
具体的

• 一个 \(Trie\) 树结点的 \(\texttt{Fail}\) 指针指向 此结点存在于 \(Trie\) 树上的最长严格后缀。
  （为了语言简洁，之后皆省略不必要话术）

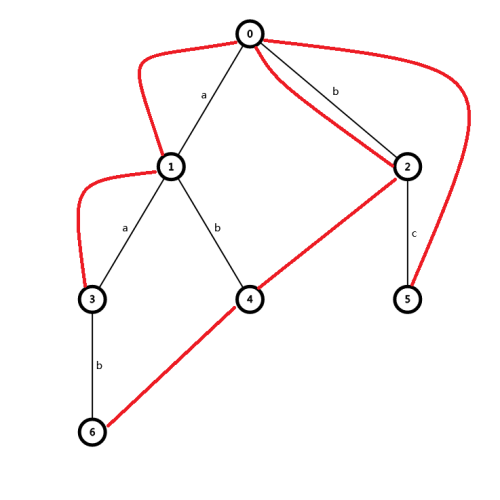
构造 \(\texttt{Fail}\) 指针

容易发现，一个结点的 \(\texttt{Fail}\) 指针指向结点深度一定小于自己，所以采用 bfs 来构建 \(Fail\) 指针。

本人比较喜欢用 \(0\) 号结点来表示 \(Tire\) 树 的根。
那么，最开始的时候，将根的所有子结点加入队列。
对于每一个点，我们执行如下操作：

当前结点的每一个子结点，它的 \(\texttt{Fail}\) 指针可能指向 当前结点的 \(\texttt{Fail}\) 指针指向结点 \(\left(v\right)\) 的对应子结点。
如果为空，则可能为 结点 \(v\) 的 \(\texttt{Fail}\) 指针指向结点的对应子结点 \(\left( v' \right)\)，如此类推。
如果都为空，则 \(Fail\) 指针指向根节点。
将子结点加入队列。

同时，我们发现，这样跳 \(\texttt{Fail}\) 指针的操作其实时间上是很劣的，我们仍然可以对其进行部分优化。
这里我们使用 路径压缩 的思想。

对于每个节点 \(u\)，我们对它的 \(ch[u][k]\) 数组定义做出修改，实质仍是一个指针数组，不过：
（我们将不进行定义修改构造出的 \(Tire\) 树叫做朴素 \(Tire\) 树）

如果朴素 \(Tire\) 树上 \(ch[u][k]\) 不为空，则 \(ch[u][k]\) 值与朴素 \(Tire\) 树相同；
否则，如果 \(ch[u][k]\) 为空，但朴素 \(Tire\) 树中存在异于 \(u\) 的一个结点 \(v\) 表示的前缀 \(S\)，是 \(u\) 表示前缀 \(T\) 的后缀，且 \(S\) 最长， \(ch[u][k]\) 指向 \(v\)。
否则， \(ch[u][k]\) 为空。

\(\texttt{Fail}\) 指针定义不变。

所以，我们可以得到如下代码

void B() {
    std::queue <int> d;
    lep(k, 0, 25) if (ch[0][k]) d.push(ch[0][k]);
    while (!d.empty()) { int u = d.front(); d.pop();
        lep(k, 0, 25) {
            if (ch[u][k]) fail[ch[u][k]] = ch[fail[u]][k], d.push(ch[u][k]);
            else ch[u][k] = ch[fail[u]][k];
        }
    }
}

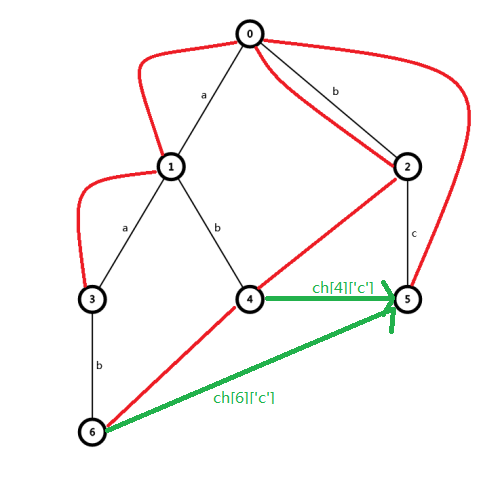
由于全部绘出指针的图片太过杂乱而难以理解，我们只针对其中的局部过程，争取获得对算法的整体把握。
（红色箭头为 \(\texttt{Fail}\) 指针，绿色箭头为改变定义后新增的用于路径压缩的指针）。
（注：编号只是为了区分结点，与实际 \(Tire\) 编号不一定相同）。

统计答案

可以发现，我们需要一个后缀和来统计答案，所以我们根据 \(\texttt{Fail}\) 指针来建一棵树，进行子树累加操作。
读者可自行考虑为什么这样可以遍历到所有后缀。

void D(int u) { for (int v : e[u]) D(v), sum[u] += sum[v]; }
void G(char s[]) {
    int len = std::strlen(s + 1), nw = 0;
    lep(i, 1, len) nw = ch[nw][s[i] - 'a'], ++sum[nw];
    lep(i, 1, idx) e[fail[i]].push_back(i);
    D(0);
    lep(i, 1, n) printf("%d\n", sum[ps[i]]);
}