2025暑假集训补题专辑

“华为智联杯”无线程序设计大赛暨2025年上海市大学生程序设计竞赛 - IJ

I. 真相

题意

给出一棵树，树的每个节点有一个人。每个人说的话都可能真可能假。 i 号节点的人说：“以我这个节点为根的子树里，有 a[i] 个人说的是真话。”现在要根据他们的话来确定哪些人说的是真话，问有多少种可能的情况。节点数不超过 5000 。

题解

这东西叫树上背包。

设 dp[i][j] 表示以 i 为根的树中有 j 个人说真话。先假设 i 这个位置的人说假话，那么对于当前树中有 j（j ≠ a[i]）个人说真话的情况，只要用每个子树中说真话的人数凑出 j 就好了。如果 j = a[i]，那么显然不能让根说假话了，所以目前 dp[i][a[i]] = 0。

如果所有子树中说真话的人数可以是 a[i] - 1，那就可以让根说真话，从而树中总共确实是 a[i] 个人说真话，成立。所以 dp[i][a[i]] = dp[i][a[i] - 1] 。

这样实际上就做完了，不需要优化。这是因为每个 i 作为根的情况只被访问一次，而在计算贡献时，每个 dp[i][j]（i 任取，j 不超过以 i 为根的子树大小）的贡献又只参与计算一次，所以 总复杂度 O(n²) ，而不是我在场上以为的 O(n³) 。

#include <bits/stdc++.h>
#define int long long
constexpr int N = 5005;
constexpr int M = 998244353;
constexpr int INF = 2e16;

int n, a[N], dp[N][N], num[N], c[N];
std::vector<int> e[N];
bool tag;

void getnum(int u, int fa) {
    num[u] = 1;
    for (int v : e[u]) {
        if (v == fa) continue;
        getnum(v, u);
        num[u] += num[v];
    }
}

void dfs(int u, int fa) {
    if (u != 1 && e[u].size() == 1) {
        if (a[u] == 1)
            dp[u][0] = 1, dp[u][1] = 1;
        else if (a[u] == 0)
            dp[u][0] = 0, dp[u][1] = 0, tag = 1;
        else {
            dp[u][0] = 1, dp[u][1] = 0;
        }
        return;
    }
    bool flag = 0;
    for (int v : e[u]) {
        if (v == fa) continue;
        dfs(v, u);
        if (!flag) {
            flag = 1;
            for (int i = 0; i <= num[v]; i++) dp[u][i] = dp[v][i];
            for (int i = num[v] + 1; i <= num[u]; i++) dp[u][i] = 0;
        } else {
            for (int i = 0; i <= num[u]; i++) c[i] = 0;
            for (int j = 0; j <= num[v]; j++) {
                for (int i = j; i <= num[u]; i++) {
                    c[i] = (c[i] + dp[u][i - j] * dp[v][j]) % M;
                }
            }
            for (int i = 0; i <= num[u]; i++) {
                dp[u][i] = c[i];
                c[i] = 0;
            }
        }
    }
    dp[u][a[u]] = (a[u] ? dp[u][a[u] - 1] : 0);
}

void solve() {
    tag = 0;
    std::cin >> n;
    for (int i = 1; i <= n; i++) std::cin >> a[i];
    if (n == 1) {
        if (a[1] == 1)
            std::cout << "2\n";
        else if (a[1] == 0)
            std::cout << "0\n";
        else
            std::cout << "1\n";
        return;
    }
    for (int i = 1; i <= n; i++) {
        e[i].clear();
    }
    for (int i = 1, u, v; i < n; i++) {
        std::cin >> u >> v;
        e[u].push_back(v);
        e[v].push_back(u);
    }
    getnum(1, 0);
    dfs(1, 0);
    if (tag) {
        std::cout << "0\n";
        return;
    }
    int sum = 0;
    for (int i = 0; i <= n; i++) sum = (sum + dp[1][i]) % M;
    std::cout << sum << "\n";
}

signed main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);
    int _ = 1;
    std::cin >> _;
    while (_--) solve();
    return 0;
}

回到顶部

J. 画圈

题意

一个简单连通无向图，每条边是白色或者黑色的。每次可以选择图中的一个环，将环上所有白边染成黑色。问最多能进行多少次这样的操作。点数范围 2e5 。

题解

如果将白边看成 “暂时不存在但是可以加入的边” ，那么对于一次加了 k 条边的操作，就可以看成：先加入 k-1 条边，不产生贡献；然后加入一条边，产生 1 的贡献。实际上也就是，每当把两个已经连通的点直接连起来，就产生 1 的贡献。

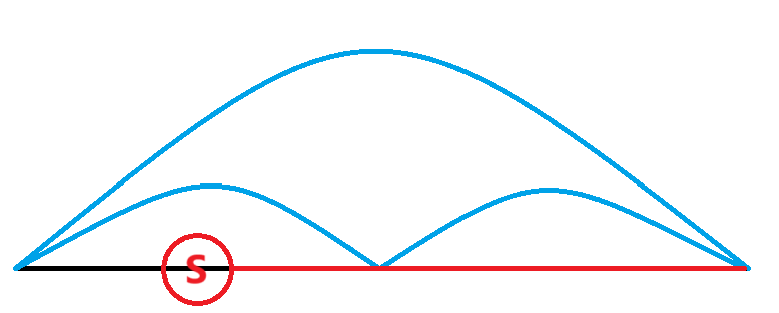
为什么这是对的呢？首先，每次操作一定是等价于先将一堆孤立点和短链连成一条长链，最后把这条长链封闭成环，所以一定有且仅有一条边产生 1 个贡献。其次，一条白边不能产生大于 1 的贡献。因为，如果假设有一条边产生了 2 的贡献，就意味着同时封闭了两条长链，如下图：

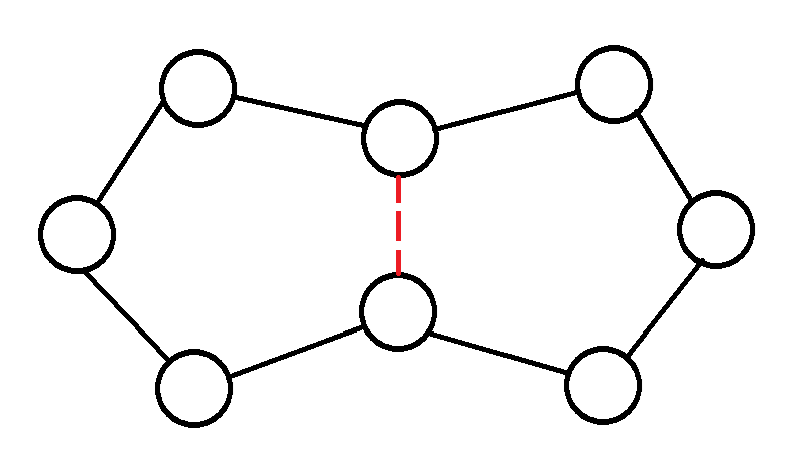
显然，这本来就是一个环，并非两条长链。

所以用并查集维护点之间的连通性，将白边依次加入，每当加入的白边的两个端点本就连通，答案就加 1 即可。

#include <bits/stdc++.h>
#define int long long
constexpr int N = 2e5 + 5;

int n, m, fa[N];
std::vector<std::pair<int, int>> w;

inline int findfa(int x) {
    return fa[x] == x ? x : fa[x] = findfa(fa[x]);
}

void solve() {
    std::cin >> n >> m;
    w.clear();
    for (int i = 1; i <= n; i++) fa[i] = i;
    for (int i = 1, u, v, c; i <= m; i++) {
        std::cin >> u >> v >> c;
        if (c)
            fa[findfa(u)] = findfa(v);
        else
            w.push_back({u, v});
    }
    int cnt = 0;
    for (auto [u, v] : w) {
        if (findfa(u) == findfa(v))
            cnt++;
        else
            fa[findfa(u)] = findfa(v);
    }
    std::cout << cnt << "\n";
}

signed main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);
    int _ = 1;
    std::cin >> _;
    while (_--) solve();
    return 0;
}

回到顶部

2025牛客暑期多校5 - EM

唉，被打爆的一场。 E 纯属没对上脑电波（完完全全的 guessforces 风）， M 属于线段树玩出花了。都该记录下。

E. Mysterious XOR Operation

题意

一个长为 n 的数组，求所有元素两两之间进行“神秘异或”运算的结果之和。 n 范围 1e5 ，每个元素范围 1e8 。

“神秘异或”定义为，先对两个数进行异或操作，然后对结果，从低位向高位遍历，去掉遇到的所有第偶数个 1 。比如， 7 和 20 的异或结果是 $(11011)_2$ ，“神秘异或”结果是 $(1001)_2$ 。

题解

考虑每一个二进制位，从低到高第 k 位对答案产生的贡献，就等于满足这个条件数对的数量：第 k 位上分别是 0 和 1 ，而且 1 到 k - 1 位异或起来有偶数个 1 。也就是说，

$\{popcount(x[1:k-1]) + popcount(y[1:k-1]) - 2 \times popcount(x[1:k-1] \& y[1:k-1])\} mod 2 == 0$

由于有模 2 ，所以减去的那项直接不用考虑。于是对于每一位，遍历这个数组，遍历到一个数时，答案加上：前面的数中，当前位和当前数的不相同，且低位 popcount 的奇偶性和当前数的相同的数的数量。就做完了。

#include <bits/stdc++.h>
#define int long long
using namespace std;

template <typename T>
class Solution {
  private:
    T *a;
    int *p;
    int n, ans;

  public:
    Solution(int n) : n(n), ans(0) {
        a = new T[n];
        p = new int[n];
        memset(p, 0, n * sizeof(int));
    }

    ~Solution() {
        delete[] a;
        delete[] p;
    }

    T &operator[](int i) { return a[i]; }

    int solve() {
        sort(a, a + n);
        for (int w = 0; w < 28; w++) {
            int oo = 0, oe = 0, zo = 0, ze = 0;
            for (int i = 0; i < n; i++) {
                if (a[i] & (1ll << w)) {
                    if (p[i] & 1)
                        ans += (1ll << w) * zo, oo++;
                    else
                        ans += (1ll << w) * ze, oe++;
                } else {
                    if (p[i] & 1)
                        ans += (1ll << w) * oo, zo++;
                    else
                        ans += (1ll << w) * oe, ze++;
                }
            }
            for (int i = 0; i < n; i++) {
                if (a[i] & (1ll << w)) p[i]++;
            }
        }
        return ans;
    }
};

signed main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    int n;
    cin >> n;
    Solution<int> sol(n);
    for (int i = 0; i < n; i++) cin >> sol[i];
    cout << sol.solve() << endl;
    return 0;
}

回到顶部

M. Mysterious Spacetime

题意

一排 x 个灯，初始全是灭的。在互不相同的、不一定连续的 n 个时刻，会有一个区间的灯全部亮起来（输入 t l r 表示在 t 时刻 [l, r] 的灯全亮）。有 m 个机器，对于每个机器，输入 l r k 表示如果某时刻 [l, r] 范围内至少有 k 个灯亮，这个机器就会启动。每个机器只会启动一次。有 q 组询问，每组输入 tl tr l r ，表示询问在 [tl, tr] 这个时间范围内，有观测范围是 [l, r] 的子区间的机器启动的最早时刻。如果没有，就是 -1 。 n m x q 范围都是 5e5 。

题解

总体思路是先求出每个机器的启动时间，然后离线处理所有询问。

下文用红线表示一台机器观测的区间，用黑线表示亮灯的区间。如果一个亮灯的区间（黑）能让一台机器（红）启动，那么有下面 4 种情况：

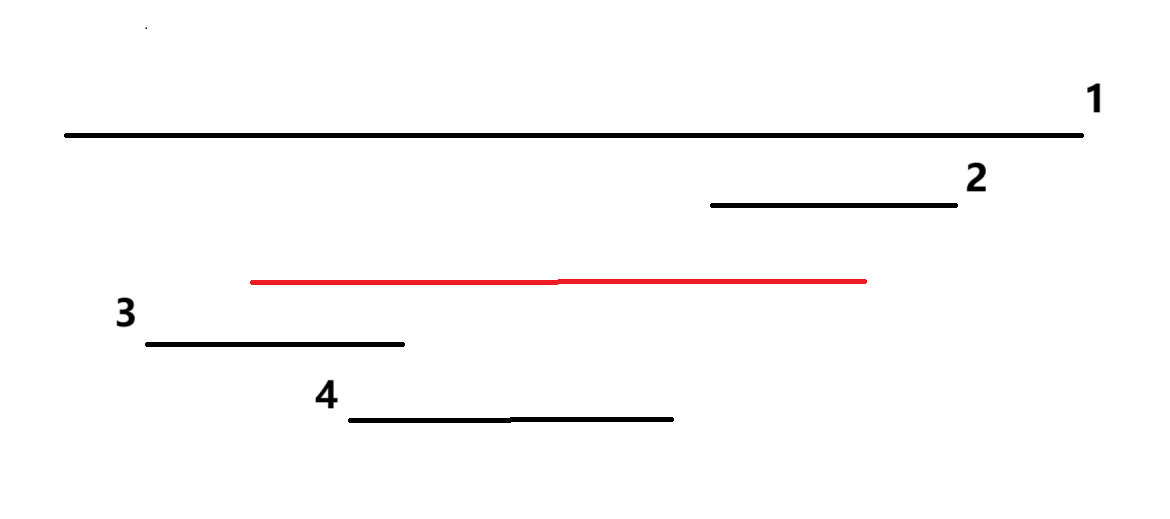
对于 1 和 2 ，可以按右端点递减的顺序遍历每条红线；每当遍历到一条 l r k 的红线，就把右端点位置大于等于它的黑线全部纳入考虑范围。如果这些黑线里有任何一个的左端点不超过 r - k + 1 ，那这个红线就能被启动。于是考虑用线段树维护区间最小值，每当将一条 t l r 的黑线纳入考虑范围，就尝试用 t 更新 l 位置的最小值。更新完毕后，当前红线的启动时间就是 [1, r - k + 1] 的最小值。

对于 3 和 4 ，可以按 k 递减的顺序遍历每条红线。设当前红线是 l r k ，将所有长度不小于 k 的黑线纳入考虑范围。由于已经保证了黑线长度足够，且 1 和 2 已经考虑过了，那么：还是线段树维护区间最小值，对于 t l r 的黑线，尝试用 t 更新 r 位置最小值。当前红线的启动时间就是 [l + k - 1, r] 的最小值。

至此已经求出了每个机器的启动时间，下面处理询问。如果一台机器是 l r k 的，且启动时间是 t ，不妨将它看作二维平面上一条线段，横坐标在 [l, r] ，纵坐标是 t ；下文中记为 sgl sgr t 的线段（ sgl 和 sgr 就是原来的 l 和 r ，仅为方便区分）。将一个 tl tr l r 的询问看作一个矩形，横向是 [l, r] ，纵向是 [tl, tr] 。那么，每次询问就是问：完全在这个矩形内部的所有线段，所带有的最小的 t 是多少。

容易想到按 t 递增考虑每个线段，将包含了当前线段的所有矩形的答案赋为 t ，然后删除这些矩形。可以按 tl 升序、类似滑动窗口的方式，保证当前在考虑范围内的矩形，都有 $t \in [tl, tr]$ 。

这就只剩下最后一个问题：给了一堆 [l, r] ，要快速找到所有满足 $[sgl, sgr] \subseteq [l, r]$ 的 [l, r] 。

最智慧的地方来了。当遍历到了一个 sgl sgr t 的线段，向考虑范围加入矩形时，用线段树/树状数组维护：左边界不超过某个位置的所有矩形中，右边界的最大值，以及这个最大值是由哪个矩形提供的。加完要考虑的所有矩形后，对于当前线段，查找左边界在 [1, sgl] 的所有矩形中右边界的最大值，以及它是哪个矩形提供的，查询结果记为 [maxr, id] 。如果 maxr > sgr ，就说明编号为 id 的这个矩形应以 t 为答案，然后被从树状数组上删除。删除后，再查 [1, sgl] ，如果还有 maxr > sgr ，就再删，直到这个条件不成立。每个矩形只会进出树状数组各一次，时间复杂度 O(qlogx) ，非常好…… 可是删了一个矩形后，如何更新前缀最大值呢？树状数组套优先队列/ set ，将每个位置的备选方案也全存下来就好了。考虑 update 过程，空间复杂度 O(mlogx) ，爆不掉，非常好。

非常 考验写代码能力 ，但我仍然认为是好题。

#include <bits/stdc++.h>
// #include <ext/pb_ds/assoc_container.hpp>
// #include <ext/pb_ds/tree_policy.hpp>
// #include <ext/pb_ds/hash_policy.hpp>

using namespace std;
// using namespace __gnu_pbds;

// #define int long long
#define ll long long
#define i128 __int128_t
#define float long double
#define ld long double
#define pii pair<int, int>
#define _(x, y) (views::iota((int)x, (int)(y + 1)))
#define __(name, ...) [&](auto const &name) { return __VA_ARGS__; }

using nli = numeric_limits<int>;
using nls = numeric_limits<signed>;
constexpr int INF = nls::max();
constexpr ld eps = 1e-12;

constexpr int N = 5e5 + 5;

int n, m, rng, qnum;
int ans[N], lans[N];

array<int, 3> e[N], g[N];
array<int, 6> s[N * 2];

int minn[N << 2];
void update(int l, int r, int u, int p, int k) {
    if (l == r) {
        minn[u] = min(minn[u], k);
        return;
    }
    int mid = (l + r) >> 1;
    if (p <= mid)
        update(l, mid, u << 1, p, k);
    else
        update(mid + 1, r, u << 1 | 1, p, k);
    minn[u] = min(minn[u << 1], minn[u << 1 | 1]);
}
int query(int l, int r, int u, int ql, int qr) {
    if (ql <= l && r <= qr) return minn[u];
    int mid = (l + r) >> 1, res = INF;
    if (ql <= mid) res = query(l, mid, u << 1, ql, qr);
    if (qr > mid) res = min(res, query(mid + 1, r, u << 1 | 1, ql, qr));
    return res;
}

array<int, 3> sg[N];
array<int, 5> sq[N];
bool gg[N];

struct qnode {
    int d, id;
    bool operator<(const qnode &qn1) const {
        if (d == qn1.d) return id > qn1.id;
        return d > qn1.d;
    }
};
priority_queue<qnode> q;

struct trnode {
    int r, id;
    bool operator<(const trnode &tn1) const {
        if (r == tn1.r) return id < tn1.id;
        return r < tn1.r;
    }
};
priority_queue<trnode> tr[N];
inline int lowbit(int x) { return x & -x; }
inline void trpush(int pos, int num, int id) {
    while (pos <= rng) {
        tr[pos].push({num, id});
        pos += lowbit(pos);
    }
}
inline trnode getmaxr(int pos) {
    trnode res = {-1, -1};
    while (pos) {
        while (!tr[pos].empty() && gg[tr[pos].top().id]) tr[pos].pop();
        if (!tr[pos].empty() && tr[pos].top().r > res.r) {
            res = tr[pos].top();
        }
        pos -= lowbit(pos);
    }
    return res;
}

inline void init() {
    for (int i = 1; i <= (rng << 2); i++) minn[i] = INF;
    for (int i = 1; i <= m; i++) ans[i] = INF;
    for (int i = 1; i <= rng; i++) {
        while (!tr[i].empty()) tr[i].pop();
    }
    for (int i = 1; i <= qnum; i++) lans[i] = INF, gg[i] = 0;
    while (!q.empty()) q.pop();
}
inline void solve() {
    cin >> n >> m >> rng >> qnum;
    init();
    for (int i = 1, t, l, r; i <= n; i++) {
        cin >> t >> l >> r;
        e[i] = {t, l, r};
    }
    for (int i = 1, l, r, k; i <= m; i++) {
        cin >> l >> r >> k;
        g[i] = {l, r, k};
    }

    for (int i = 1; i <= n; i++) {
        auto [t, l, r] = e[i];
        s[i] = {l, r, 1, t, i, r - l + 1};
    }
    for (int i = 1; i <= m; i++) {
        auto [l, r, k] = g[i];
        s[n + i] = {l, r, 2, k, i, k};
    }
    sort(s + 1, s + 1 + n + m, [&](auto a1, auto a2) {
        if (a1[1] == a2[1]) return a1[2] < a2[2];
        return a1[1] > a2[1];
    });
    for (int i = 1; i <= n + m; i++) {
        auto [l, r, f, x, id, len] = s[i];
        if (f == 1)
            update(1, rng, 1, l, x);
        else
            ans[id] = query(1, rng, 1, 1, r - x + 1);
    }

    for (int i = 1; i <= (rng << 2); i++) minn[i] = INF;
    sort(s + 1, s + 1 + n + m, [&](auto a1, auto a2) {
        if (a1[5] == a2[5]) return a1[2] < a2[2];
        return a1[5] > a2[5];
    });
    for (int i = 1; i <= n + m; i++) {
        auto [l, r, f, x, id, len] = s[i];
        if (f == 1)
            update(1, rng, 1, r, x);
        else
            ans[id] = min(ans[id], query(1, rng, 1, l + x - 1, r));
    }

    for (int i = 1; i <= m; i++) sg[i] = {g[i][0], g[i][1], ans[i]};
    for (int i = 1, u, d, l, r; i <= qnum; i++) {
        cin >> u >> d >> l >> r;
        sq[i] = {u, d, l, r, i};
    }
    sort(sg + 1, sg + 1 + m, [&](auto a1, auto a2) {
        return a1[2] < a2[2];
    });
    sort(sq + 1, sq + 1 + qnum, [&](auto a1, auto a2) {
        return a1[0] < a2[0];
    });

    int cur = 1;
    for (int i = 1; i <= m; i++) {
        auto [sgl, sgr, sgt] = sg[i];
        if (sgt == INF) break;
        while (cur <= qnum && sq[cur][0] <= sgt) {
            trpush(sq[cur][2], sq[cur][3], sq[cur][4]);
            q.push({sq[cur][1], sq[cur][4]});
            cur++;
        }
        while (!q.empty() && q.top().d < sgt) {
            gg[q.top().id] = 1;
            q.pop();
        }
        while (1) {
            auto [maxr, sqid] = getmaxr(sgl);
            if (maxr < sgr) break;
            lans[sqid] = sgt;
            gg[sqid] = 1;
        }
    }

    for (int i = 1; i <= qnum; i++) {
        cout << (lans[i] == INF ? -1 : lans[i]) << endl;
    }
}

signed main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    int _ = 1;
    cin >> _;
    while (_--) solve();
    return 0;
}

回到顶部

The 3rd Universal Cup. Stage 18: Southeastern Europe - F

天哪，从不到 3h 开始做这个题，一直调到 4h+ ，突然发现做法假透了。崩溃的一局。

F. Magical Bags

抽象后的题意

给出数轴上的 n 个线段，每个线段的左右两端以及中间标了一些特殊点（这里说的“线段”可以是一个单独的特殊点）。如果去掉一条线段上的一些特殊点，它的跨度就会变成：从最靠左的没被去掉的特殊点，到最靠右的一个。保证所有线段的所有特殊点的位置各不相同。问至少保留几个点，使得原本有重叠的线段仍然有重叠。 n 范围 2e5 ；特殊点不超过 5e5 个，位置跨度可以很大。

题解

如果将单点看成左右端点相同的线段，那么显然，每条线段上至多保留两个点，也就是两个端点。只需要考虑最多有多少个线段可以只保留一个点，就能得出答案。

首先判断一下有哪些线段满足：只将这条线段缩成一个点，其他线段不变，是合法的。外层遍历每条线段（假设当前线段左右端点分别是 l, r），内层遍历这个线段上的每个点（假设当前点位于 x ），如果 [l, x] 内有其他线段的右端点，或者 [x, r] 内有其他线段的左端点，那么把 [l, r] 缩成 x 就是不合法的。如果一条线段上有一个点合法，那么这个线段就是可以缩的。

由于每个关键点的位置各不相同，所以两条线段缩了之后一定不相交。所以，只有本来就不相交的线段可以同时缩，问题就变成了在满足上一段的条件的线段中选取尽可能多的，使得它们都不相交。很典的贪心：将所有线段按右端点升序排序，枚举，如果当前线段和上一条不相交，就选它，答案是最优的。

#include <bits/stdc++.h>
// #include <ext/pb_ds/assoc_container.hpp>
// #include <ext/pb_ds/tree_policy.hpp>
// #include <ext/pb_ds/hash_policy.hpp>

using namespace std;
// using namespace __gnu_pbds;

#define int long long
#define ll long long
#define i128 __int128_t
#define float long double
#define ld long double
#define pii pair<int, int>
#define _(x, y) (views::iota((int)x, (int)(y + 1)))
#define __(name, ...) [&](auto const &name) { return __VA_ARGS__; }

using nli = numeric_limits<int>;
using nls = numeric_limits<signed>;
constexpr int INF = nli::max();
constexpr ld eps = 1e-12;

constexpr int N = 2e5 + 5;

int n;
vector<int> a[N];
set<int> minn, maxn;
bool f[N];

struct seg {
    int l, r, id;
} s[N];

inline void init() {
}
inline void solve() {
    cin >> n;
    for (int i = 1, k, x; i <= n; i++) {
        cin >> k;
        while (k--) {
            cin >> x;
            a[i].push_back(x);
        }
        sort(a[i].begin(), a[i].end());
        minn.insert(a[i].front()), maxn.insert(a[i].back());
    }

    auto checkl = [&](int l, int r) -> bool {
        auto it = maxn.upper_bound(l);
        return !(it != maxn.end() && *it < r);
    };
    auto checkr = [&](int l, int r) -> bool {
        auto it = minn.upper_bound(l);
        return !(it != minn.end() && *it < r);
    };
    int tot = 0;
    for (int i = 1; i <= n; i++) {
        int l = a[i].front(), r = a[i].back();
        for (int u : a[i]) {
            if (checkl(l, u) && checkr(u, r)) {
                s[++tot] = {l, r, i};
                break;
            }
        }
    }

    sort(s + 1, s + 1 + tot, [&](seg s1, seg s2) {
        return s1.r < s2.r;
    });
    f[s[1].id] = 1;
    int lastr = s[1].r;
    for (int i = 2; i <= tot; i++) {
        if (s[i].l < lastr) continue;
        f[s[i].id] = 1;
        lastr = s[i].r;
    }

    int ans = 0;
    for (int i = 1; i <= n; i++) ans += f[i] ? 1 : 2;
    cout << ans << endl;
}

signed main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    int _ = 1;
    // cin >> _;
    while (_--) solve();
    return 0;
}

回到顶部

The 3rd Universal Cup. Stage 35: Kraków - J

J. Sumotonic Sequences

题意

给一个长为 n 的数组，有 q 次操作，每次操作输入 l r s d ，表示将数组的 [l, r] 这个区间加上一个首项为 s 、公差为 d 的等差数列。具体地：

$s_l$ += $s$ ， $s_{l+1}$ += $s$ + $d$ ， $s_{l+2}$ += $s$ + $2d$ ，……， $s_r$ += $s$ + ($r$ - $l$) $d$

问初始数组，以及每次操作后的数组，是否可以表示成若干个单调不减的非负数组和若干个单调不增的非负数组之和。 n 和 q 范围都是 2e5 。

题解

显然，题目条件等价于表示成一个单调不减非负数组 $inc$ 和一个单调不增非负数组 $dec$ ，它们由若干个同类数组全部加起来得到的。然后考虑区间加等差数列这个操作，容易想到用维护原数组的差分数组（记为 $a$ ），那么题中操作就变成了

$a_l$ += s ， $a_{[l+1 : r]}$ += $d$ ， $a_{r+1}$ -= $s$ + ($r$ - $l$) $d$

$inc$ 的差分数组，每一项都应非负；而 $dec$ 的差分数组应满足首项非负、其余每一项非正、所有元素和非负。如果原数组的差分数组能表示成这样的两个差分数组之和，即满足题中条件。这里，约束最强的条件就是 $dec$ 的 “所有元素和非负” ，也就是说应让 $\sum dec_i$ 尽可能大。由于 $a_i = inc_i + dec_i$ ，所以最优方案就是 $dec_1 = a_1$ ； $dec_i = min(0, a_i), i \in [2, n]$ 。此时 $inc$ 自然满足要求。

至此，题目化简为： 维护一个数组，支持区间加（每次操作是：操作数非负，单点加、区间加、单点减）和查询所有负数之和 。上面都是简单的，下面才是难点（然而题解刚好没说接下来具体怎么做！！！只给了个大致方向）。

一种相对简单的方法是，线段树维护区间非负数个数、非负数之和、负数最大值（代码中的 psum, pcnt, nmax）。区间加的时候，如果当前来到的区间最大负数加操作数后仍为负数，就只更新区间信息、打 tag ，否则向下递归。当递归到了一个单独的、正负性发生改变的数，……这里看代码吧。由于每次操作只有一个位置变小，故正负性改变次数是线性级别的，时间复杂度 O((n + q) log n) ，可以通过。

#include <bits/stdc++.h>
// #include <ext/pb_ds/assoc_container.hpp>
// #include <ext/pb_ds/tree_policy.hpp>
// #include <ext/pb_ds/hash_policy.hpp>

using namespace std;
// using namespace __gnu_pbds;

#define int long long
#define ll long long
#define i128 __int128_t
#define float long double
#define ld long double
#define pii pair<int, int>
#define _(x, y) (views::iota((int)x, (int)(y + 1)))
#define __(name, ...) [&](auto const &name) { return __VA_ARGS__; }

using nli = numeric_limits<int>;
using nls = numeric_limits<signed>;
constexpr int INF = 2e16;
constexpr ld eps = 1e-12;

constexpr int N = 2e5 + 5;

int n, qnum, a[N];
int psum[N << 2], pcnt[N << 2], nmax[N << 2], add[N << 2];

inline void pushup(int u) {
    psum[u] = psum[u << 1] + psum[u << 1 | 1], pcnt[u] = pcnt[u << 1] + pcnt[u << 1 | 1];
    nmax[u] = max(nmax[u << 1], nmax[u << 1 | 1]);
}
inline void pushdown(int u) {
    if (!add[u]) return;
    psum[u << 1] += add[u] * pcnt[u << 1], psum[u << 1 | 1] += add[u] * pcnt[u << 1 | 1];
    nmax[u << 1] += add[u], nmax[u << 1 | 1] += add[u];
    add[u << 1] += add[u], add[u << 1 | 1] += add[u];
    add[u] = 0;
}

void build(int l, int r, int u) {
    add[u] = 0;
    if (l == r) {
        if (a[l] >= 0)
            psum[u] = a[l], pcnt[u] = 1, nmax[u] = -INF;
        else
            psum[u] = 0, pcnt[u] = 0, nmax[u] = a[l];
        return;
    }
    int mid = (l + r) >> 1;
    build(l, mid, u << 1), build(mid + 1, r, u << 1 | 1);
    pushup(u);
}

void update(int l, int r, int u, int ql, int qr, int k) {
    if (ql <= l && r <= qr) {
        if (l == r) {
            if (k > 0) {
                if (pcnt[u])
                    psum[u] += k;
                else {
                    if (nmax[u] + k >= 0)
                        psum[u] = nmax[u] + k, pcnt[u] = 1, nmax[u] = -INF;
                    else
                        nmax[u] += k;
                }
            } else {
                if (pcnt[u]) {
                    if (psum[u] + k < 0)
                        nmax[u] = psum[u] + k, psum[u] = pcnt[u] = 0;
                    else
                        psum[u] += k;
                } else
                    nmax[u] += k;
            }
            return;
        }
        if (nmax[u] + k < 0) {
            psum[u] += k * pcnt[u], nmax[u] += k, add[u] += k;
            return;
        }
    }
    int mid = (l + r) >> 1;
    pushdown(u);
    if (ql <= mid) update(l, mid, u << 1, ql, qr, k);
    if (qr > mid) update(mid + 1, r, u << 1 | 1, ql, qr, k);
    pushup(u);
}

inline void init() {
    for (int i = 0; i <= (n << 2); i++) {
        psum[i] = pcnt[i] = nmax[i] = add[i] = 0;
    }
}
inline void solve() {
    cin >> n >> qnum;
    init();
    for (int i = 1; i <= n; i++) cin >> a[i];
    for (int i = n; i > 1; i--) a[i] -= a[i - 1];
    int hd = a[1], sum = 0;
    for (int i = 1; i <= n; i++) sum += a[i];
    build(1, n, 1);
    cout << (hd + (sum - psum[1]) >= 0 ? "YES" : "NO") << endl;

    int l, r, s, d;
    while (qnum--) {
        cin >> l >> r >> s >> d;
        update(1, n, 1, l, l, s);
        if (l < r) update(1, n, 1, l + 1, r, d);
        if (r < n) update(1, n, 1, r + 1, r + 1, -(s + (r - l) * d));
        if (l == 1) hd += s;
        if (r == n) sum += s + (r - l) * d;
        cout << (hd + (sum - psum[1]) >= 0 ? "YES" : "NO") << endl;
    }
}

signed main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    int _ = 1;
    cin >> _;
    while (_--) solve();
    return 0;
}

回到顶部

The 3rd Universal Cup. Stage 21: Ōokayama - ABCEM

虽然我们队牢底坐穿了吧，但这场的可做题其实不少，还都挺有意思的。

A. Don't Detect Cycle

题意

给出一个包含 m 条无向边的集合，保证这 m 条边能构成一个简单图。初始图中没有边，只是 n 个孤立点，问能不能把这 m 条边按某个顺序加入图中，使得即将添加每一条边的时候，它的两个端点均不参与构成环。如果能，输出一个加边顺序；否则输出 -1 。 n 和 m 范围都是 4000 。

题解

首先，割边不参与构成环，它们存在与否并不影响其他边添加时的合法性，所以可以直接把图中所有割边作为最先添加的一些边，然后假装它们不存在。

删去割边之后，图里就只剩下环结构，可以是单个环，也可以是几个环堆叠在一起。考虑最后添加的那条边，把它加到图中，实际上就是封闭了若干个环，就像下面这样（红色的是当前考虑的边）：

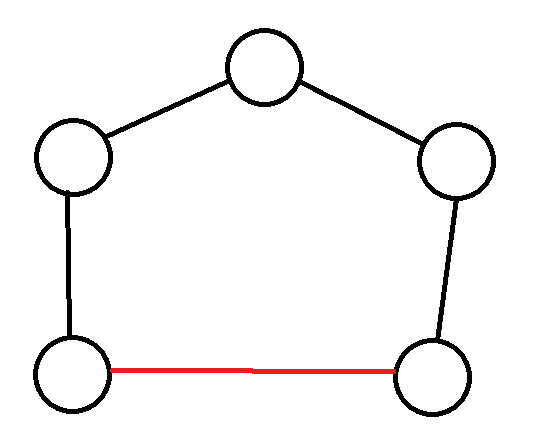
封闭一个环

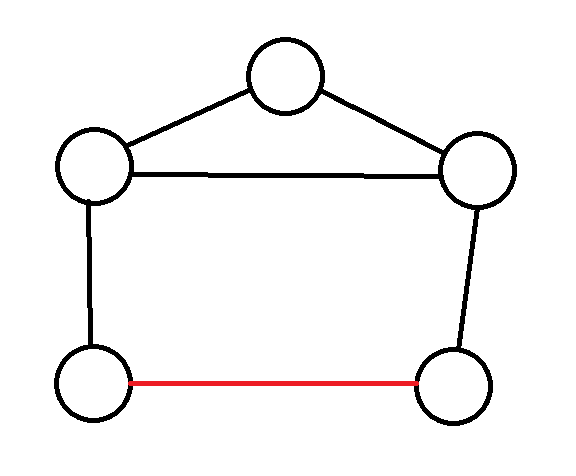
封闭两个环

也就是说，如果一条边在添加之前，它的两个端点度数均不超过 1 ，我们就可以把它作为最后添加的边。因为是最后添加的，此前它一直不存在，所以在处理其余边时，就不用考虑它，直接把它删掉即可。

重复执行上述过程，删割边、删封闭环的边，直到把所有边都删掉为止。每轮都会有边被删，不然无解，所以时间复杂度不超过 $O(m^2)$ 。

#include <bits/stdc++.h>
// #include <ext/pb_ds/assoc_container.hpp>
// #include <ext/pb_ds/tree_policy.hpp>
// #include <ext/pb_ds/hash_policy.hpp>

using namespace std;
// using namespace __gnu_pbds;

#define int long long
#define ll long long
#define i128 __int128_t
#define float long double
#define ld long double
#define pii pair<int, int>
#define _(x, y) (views::iota((int)x, (int)(y + 1)))
#define __(name, ...) [&](auto const &name) { return __VA_ARGS__; }

using nli = numeric_limits<int>;
using nls = numeric_limits<signed>;
constexpr int INF = 2e16;
constexpr ld eps = 1e-12;

constexpr int N = 5005;

int n, m, deg[N], dfn[N], low[N], tot;
vector<pii> e[N];
vector<int> q, h;
pii b[N];
bool f[N];

void dfs(int u, int from) {
    dfn[u] = low[u] = ++tot;
    for (auto [v, w] : e[u]) {
        if (f[w]) continue;
        if (!dfn[v]) {
            dfs(v, u);
            low[u] = std::min(low[u], low[v]);
            if (low[v] > dfn[u]) {
                f[w] = 1;
                q.push_back(w);
                deg[u]--, deg[v]--;
            }
        } else if (v != from)
            low[u] = std::min(low[u], dfn[v]);
    }
}

inline void init() {
    for (int i = 1; i <= max(n, m); i++) {
        e[i].clear();
        deg[i] = 0;
        f[i] = 0;
    }
    q.clear(), h.clear();
}
inline void solve() {
    cin >> n >> m;
    init();
    for (int i = 1, u, v; i <= m; i++) {
        cin >> u >> v;
        e[u].emplace_back(v, i);
        e[v].emplace_back(u, i);
        deg[u]++, deg[v]++;
        b[i] = {u, v};
    }
    int cnt = 0;
    while (1) {
        bool flag = 0;
        for (int i = 1; i <= m; i++) {
            if (!f[i]) {
                flag = 1;
                break;
            }
        }
        if (!flag) break;
        cnt++;
        if (cnt > m + 5) break;
        tot = 0;
        for (int i = 1; i <= n; i++) dfn[i] = 0, low[i] = 0;
        for (int i = 1; i <= n; i++) {
            if (!dfn[i]) dfs(i, i);
        }
        for (int i = 1; i <= m; i++) {
            if (f[i]) continue;
            auto [u, v] = b[i];
            if (deg[u] > 2 || deg[v] > 2) continue;
            f[i] = 1;
            h.push_back(i);
            deg[u]--, deg[v]--;
        }
    }
    if (cnt > m + 5) {
        cout << -1 << endl;
        return;
    }
    for (int u : q) cout << u << " ";
    for (int i = h.size() - 1; i >= 0; i--) cout << h[i] << " ";
    cout << endl;
}

signed main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    int _ = 1;
    cin >> _;
    while (_--) solve();
    return 0;
}

回到顶部

B. Self Checkout

就不细写了，只要知道下面这个结论，这题就做完了。

一个小结论

(1) 边长为 n 的网格，从左下角走到右上角，对角线以上的位置（下图中紫色的格子）不能走，方案数是：

\[\binom{2n}{n} - \binom{2n}{n-2} \]

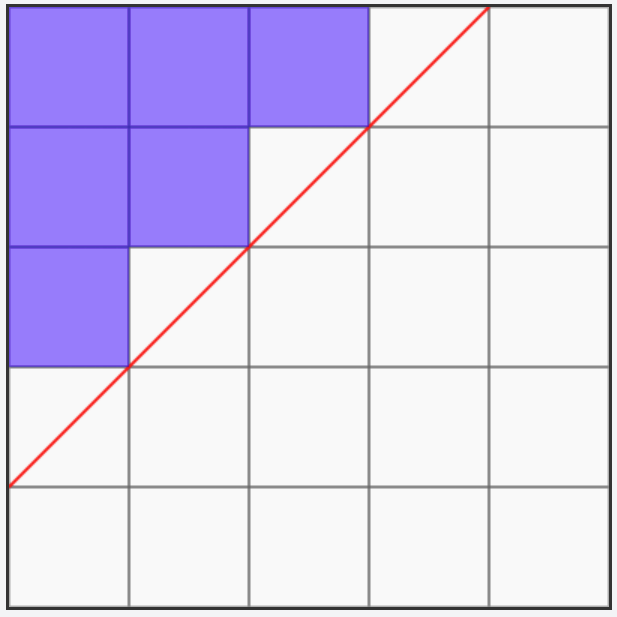
(2) 长 n 宽 m （n > m）的网格，还是紫色的位置不能走，方案数是：

\[\binom{n+m}{n} - \binom{n+m}{m-2} \]

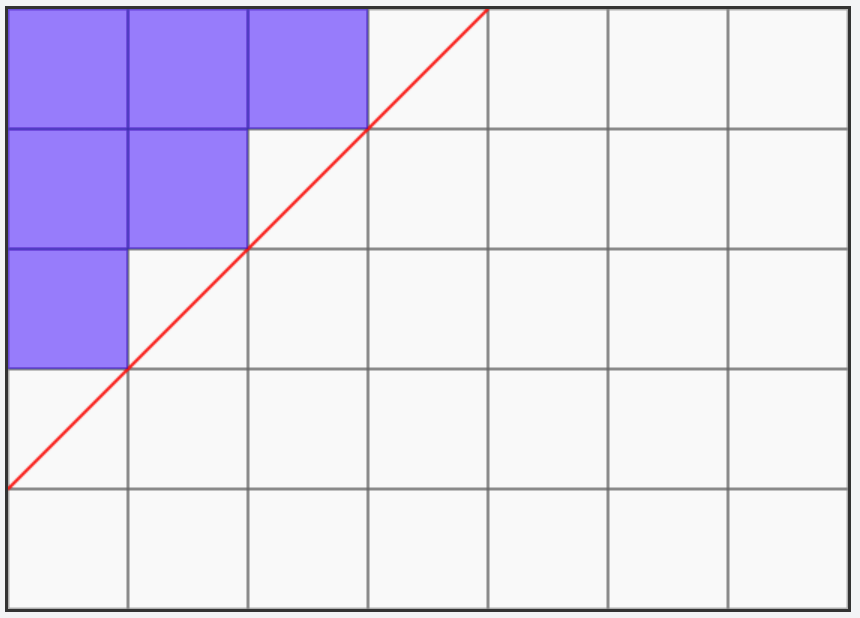
可见 (2) 是 (1) 的一般形式。

回到顶部

C. Segment Tree

题意

给定一个最底层有 $2^N$ 个点的、像线段树一样的无向图，比如下图就是 $N=3$ 的情况，底层的点和每一层的边的编号都是给定的。

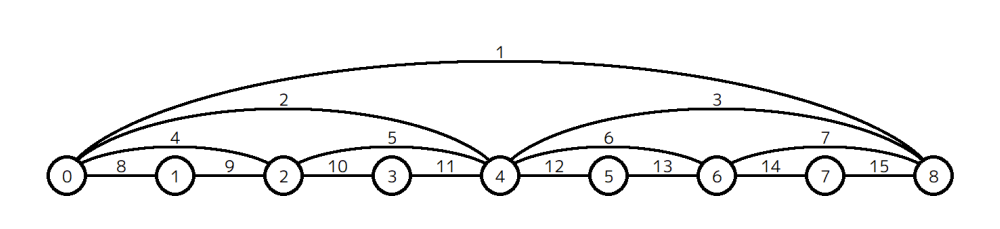
输入每条边的初始长度，然后有 Q 次操作，分两种： 1 j x ，表示把 j 号边的长度改为 x ； 2 s t 表示查询从 s 号点到 t 号点的最短路（s < t）。 N 上限 18 ， Q 上限 2e5 。

题解

先想想如何快速查询。每一次查询，答案就是从 s 出发，先到达包含 s 的某个区间（指两端被一条边连接的连续的一段点）的右端点，然后经过若干个极大区间，到达包含 t 的某个区间的左端点，最后到达 t 。

于是就需要维护每一条边的两个端点之间的最短路。考虑将这个区间按题中给定的方式拆成两个极大子区间，当前区间的最短路就是两个子区间各自端点之间的最短路之和。可见，初始化和修改都和线段树同理。这样，就解决了修改操作。

接下来考虑查询操作。不妨考虑按线段树的方式查询，初始时是这样：

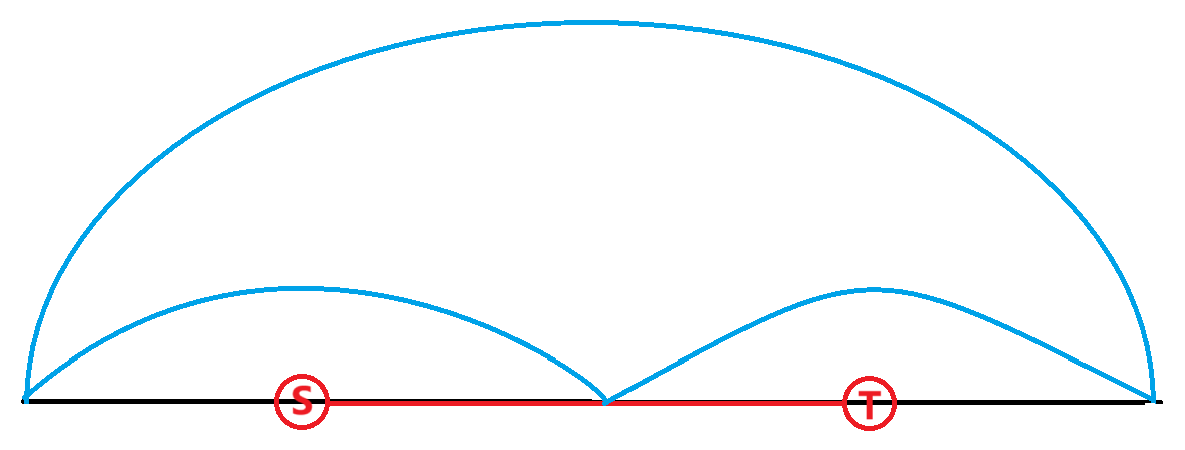
一种方案是从 s 先到左子区间的右端点，也就是右子区间的左端点，最后到 t ；另一种方案是先到左子区间的左端点，再通过整个区间的最短路（1. 是最短路，而不是长边；2. 这个是已经维护了的）跨到右子区间的右端点，最后到 t 。假设从 s 到左子区间两端（左和右，不是或）的最短路，和从 t 到右子区间两端的最短路都已经求出，那么如果用当前区间最短路，答案来自第二种方案；如果不用，答案来自第一种方案。二者取 min 即可。接下来考虑向左分治：

如果 s 还是在左子区间，而现在是要到整个区间的右端点，那么答案就是：从 s 到左子区间右端点再到最右端（第二步是已经维护了的），或者从 s 到左子区间左端点然后通过整个区间的最短路到右端点。继续向左分治即可。

递归下来之后 s 在右子区间的情况与之同理，左子区间为空，只有向左走会对答案产生贡献。对 t 那边，也是同理，就是左右翻转了一下而已。接下来大力分讨转移式子就做完了。

直接写分讨当然可以，但是各种情况可以归纳成下面代码的 query 函数里的转移方程，非常简洁。

#include <bits/stdc++.h>
// #include <ext/pb_ds/assoc_container.hpp>
// #include <ext/pb_ds/tree_policy.hpp>
// #include <ext/pb_ds/hash_policy.hpp>

using namespace std;
// using namespace __gnu_pbds;

#define int long long
#define ll long long
#define i128 __int128_t
#define float long double
#define ld long double
#define pii array<int, 2>
#define _(x, y) (views::iota((int)x, (int)(y + 1)))
#define __(name, ...) [&](auto const &name) { return __VA_ARGS__; }

using nli = numeric_limits<int>;
using nls = numeric_limits<signed>;
constexpr int INF = 2e16;
constexpr ld eps = 1e-12;

constexpr int N = 1e6 + 5;

int n, c[N], dp[N], qnum;

pii query(int l, int r, int u, int ql, int qr) {
    if (r <= ql || qr <= l) return {0, dp[u]};
    if (ql <= l && r <= qr) return {dp[u], 0};
    int mid = (l + r) >> 1;
    pii a = query(l, mid, u << 1, ql, qr), b = query(mid, r, u << 1 | 1, ql, qr);
    return {min(a[0] + b[0], a[1] + b[1] + dp[u]), min(a[1] + b[1], a[0] + b[0] + dp[u])};
}

inline void solve() {
    cin >> n;
    for (int i = 1; i < (1 << (n + 1)); i++) cin >> c[i];
    for (int i = (1 << n); i < (1 << (n + 1)); i++) dp[i] = c[i];
    for (int i = (1 << n) - 1; i >= 1; i--) dp[i] = min(c[i], dp[i << 1] + dp[i << 1 | 1]);
    cin >> qnum;
    while (qnum--) {
        int op;
        cin >> op;
        if (op == 1) {
            int j, x;
            cin >> j >> x;
            c[j] = x;
            for (int i = j; i >= 1; i >>= 1) {
                if (i >= (1 << n))
                    dp[i] = c[i];
                else
                    dp[i] = min(c[i], dp[i << 1] + dp[i << 1 | 1]);
            }
        } else {
            int ql, qr;
            cin >> ql >> qr;
            cout << query(0, 1 << n, 1, ql, qr)[0] << endl;
        }
    }
}

signed main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    int _ = 1;
    // cin >> _;
    while (_--) solve();
    return 0;
}

回到顶部

E. ReTravel

题意

给出平面直角坐标系中 n 个坐标非负的点，要从原点出发，按输入的顺序走到这些点，求最小花费。规则如下：

向右走一步花费为 1 ，然后记下一个 X ；向上走一步花费也是 1 ，然后记下一个 Y ；只有最后记录的字母是 X 时才能向左走，花费为 0 ，然后删除这个记录；只有最后记录的字母是 Y 时才能向下走，花费为 0 ，然后删除这个记录。也就是说，如果想向左或向下走，必须沿着刚刚向右和向上走的轨迹回退。 n 范围 500 。

题解

考虑区间 DP 。~~不懂怎么能顺利想到区间 DP 。~~ 令 minx[l][r] 和 miny[l][r] 表示下标在 [l, r] 的所有点中最小的横纵坐标； dp[l][r] 表示从 (minx[l][r], miny[l][r]) 这个点（下文称为“左下角”）出发，依次访问下标在 [l, r] 的每个点的最小花费（下文称为“答案”）。

显然，任意 dp[i][i] = 0 。为求一个 dp[l][r] （$l \neq r$），可以将 [l, r] 分为两个子区间，合并它们的答案。假设分为了 [l, i] 和 [i + 1, r] ，且已知这两个子区间的答案，那么在这种分割方案下，能得到 [l, r] 的答案的走法之一是：从 [l, r] 的左下角出发，走到 [l, i] 的左下角，然后依次访问 [l, i] 这些点，然后回退到 [l, r] 的左下角，再走到 [i + 1, r] 的左下角，依次访问 [i + 1, r] 的点。至此就做完了。

#include <bits/stdc++.h>
// #include <ext/pb_ds/assoc_container.hpp>
// #include <ext/pb_ds/tree_policy.hpp>
// #include <ext/pb_ds/hash_policy.hpp>

using namespace std;
// using namespace __gnu_pbds;

#define int long long
#define ll long long
#define i128 __int128_t
#define float long double
#define ld long double
#define pii array<int, 2>
#define _(x, y) (views::iota((int)x, (int)(y + 1)))
#define __(name, ...) [&](auto const &name) { return __VA_ARGS__; }

using nli = numeric_limits<int>;
using nls = numeric_limits<signed>;
constexpr int INF = 2e16;
constexpr ld eps = 1e-12;

constexpr int N = 505;

int n, dp[N][N], minx[N][N], miny[N][N], x[N], y[N];

inline void init() {
}
inline void solve() {
    cin >> n;
    for (int i = 1; i <= n; i++) cin >> x[i] >> y[i];
    for (int i = 1; i <= n; i++) {
        minx[i][i] = x[i];
        miny[i][i] = y[i];
        for (int j = i + 1; j <= n; j++) {
            minx[i][j] = min(minx[i][j - 1], x[j]);
            miny[i][j] = min(miny[i][j - 1], y[j]);
        }
    }
    for (int i = 1; i < n; i++) {
        for (int j = i + 1; j <= n; j++) dp[i][j] = INF;
    }
    for (int i = 1; i <= n; i++) dp[i][i] = 0;
    for (int len = 2; len <= n; len++) {
        for (int l = 1; l + len - 1 <= n; l++) {
            int r = l + len - 1;
            for (int i = l; i < r; i++)
                dp[l][r] = min(dp[l][r], minx[l][i] + miny[l][i] + minx[i + 1][r] + miny[i + 1][r] - (minx[l][r] + miny[l][r]) * 2 + dp[l][i] + dp[i + 1][r]);
        }
    }
    cout << dp[1][n] + minx[1][n] + miny[1][n] << endl;
}

signed main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    int _ = 1;
    // cin >> _;
    while (_--) solve();
    return 0;
}

回到顶部

M. Cartesian Trees

题意

给出一个长为 n 的数组，以及这个数组的 q 个子数组（用区间表示）。问，如果用每一个子数组建一棵笛卡尔树，有多少棵互不同构？ n 和 q 范围都是 4e5 。

题解

首先，不考虑位置，只判断是否同构，这就是树哈希用来解决的问题，因此不难想到哈希。本题如果使用树哈希，那么相邻的区间的合并或者差分都是困难的，因此需要考虑其他的哈希形式。

考虑用输入的区间构造出的一棵笛卡尔树上的一个点。“在构成树的这个区间里它们的左/右侧是否有比它小的点？如果有，下标之差是多少？”如果两棵笛卡尔树同构，那么任意一组对应的点，这个东西显然是相同的；反之，至少存在一组对应的点，这个东西不同。

因为询问的是多个可重叠的连续区间，因此不难想到差分求哈希值。怎么差分？如果将整个数组看成一个某进制的数，每一位上的“信息”是这位的值，然后维护前缀哈希值，就可以差分了。这样，两个同构的区间的哈希值，较大的一个一定是较小的一个乘上进制的若干次方。对此，只需在求出每个区间的哈希值后，根据起始/结束位置，乘上进制的若干次方，“对齐”一下即可。

下面的代码采用的哈希方法是：设位置 i 左边第一个数值比它小的位置是 l[i] ，右边第一个是 r[i] （如果不存在就是0），形成两种二元组 [l[i], i] 、 [i, r[i]] 。将它们分别按右端点排序，然后从小到大遍历。每遍历到一个位置，就把所有以它为右端点的二元组的左端点加上“距离 × 进制数” ，然后差分求出以它为右端点的区间的哈希值，存到 set 里自动去重。~~（借鉴自黄大爷的博客，只能说tql）~~

#include <bits/stdc++.h>
// #include <ext/pb_ds/assoc_container.hpp>
// #include <ext/pb_ds/tree_policy.hpp>
// #include <ext/pb_ds/hash_policy.hpp>

using namespace std;
// using namespace __gnu_pbds;

#define int long long
#define ll long long
#define i128 __int128_t
#define float long double
#define ld long double
#define pii array<int, 2>
#define _(x, y) (views::iota((int)x, (int)(y + 1)))
#define __(name, ...) [&](auto const &name) { return __VA_ARGS__; }

using nli = numeric_limits<int>;
using nls = numeric_limits<signed>;
constexpr int INF = 2e16;
constexpr ld eps = 1e-12;

constexpr int N = 4e5 + 5;
constexpr int B1 = 233, M1 = 1e9 + 9, B2 = 163, M2 = 1e9 + 7;

int n, a[N], qnum, l[N], r[N];
pii q[N];
int pw1[N], pw2[N];
int stk[N], tp;
vector<pii> bukl[N], bukr[N];
set<pii> stat;

class BIT {
  private:
    int tr[N];

  public:
#define lowbit(x) (x & -x)

    inline void update(int p, int k, int M) {
        while (p <= n) {
            (tr[p] += k) %= M;
            p += lowbit(p);
        }
    }

    inline int query(int p, int M) {
        int res = 0;
        while (p) {
            (res += tr[p]) %= M;
            p -= lowbit(p);
        }
        return res;
    }
#undef lowbit
} trl, trr;

inline void init() {
    pw1[1] = pw2[1] = 1;
    for (int i = 2; i <= n; i++) {
        pw1[i] = pw1[i - 1] * B1 % M1;
        pw2[i] = pw2[i - 1] * B2 % M2;
    }
}
inline void solve() {
    cin >> n;
    init();
    for (int i = 1; i <= n; i++) cin >> a[i];
    tp = 0;
    for (int i = 1; i <= n; i++) {
        while (tp && a[stk[tp]] > a[i]) tp--;
        l[i] = stk[tp];
        stk[++tp] = i;
    }
    tp = 0;
    for (int i = n; i >= 1; i--) {
        while (tp && a[stk[tp]] > a[i]) tp--;
        r[i] = stk[tp];
        stk[++tp] = i;
    }
    for (int i = 1; i <= n; i++) {
        if (l[i]) bukl[i].push_back({l[i], pw1[i] * (i - l[i]) % M1});
        if (r[i]) bukr[r[i]].push_back({i, pw2[i] * (r[i] - i) % M2});
    }

    cin >> qnum;
    for (int i = 1; i <= qnum; i++) cin >> q[i][0] >> q[i][1];
    sort(q + 1, q + 1 + qnum, [&](pii q1, pii q2) { return q1[1] < q2[1]; });
    int cur = 1;
    for (int i = 1; i <= n; i++) {
        for (auto [p, k] : bukl[i]) trl.update(p, k, M1);
        for (auto [p, k] : bukr[i]) trr.update(p, k, M2);
        while (cur <= qnum && q[cur][1] <= i) {
            int hsh1 = (trl.query(i, M1) - trl.query(q[cur][0] - 1, M1) + M1) % M1 * pw1[n - q[cur][0] + 1] % M1;
            int hsh2 = (trr.query(i, M2) - trr.query(q[cur][0] - 1, M2) + M2) % M2 * pw2[n - q[cur][0] + 1] % M2;
            stat.insert({hsh1, hsh2});
            cur++;
        }
    }
    cout << stat.size() << endl;
}

signed main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    int _ = 1;
    // cin >> _;
    while (_--) solve();
    return 0;
}

回到顶部

2025杭电暑期多校10 - 1002

1002. Multiple and Factor

题意

给定一个长度为 $n$ 的序列 $a$ ，需要支持以下四种操作：

1 x k：给 $x$ 倍数的下标位置上的值加 $k$ 。
2 x k：给 $x$ 因数的下标位置上的值加 $k$ 。
3 x：查询 $x$ 倍数的下标位置上所有数的和。
4 x：查询 $x$ 因数的下标位置上所有数的和。

题解

容易想到，将所有操作按 $x \leq \sqrt{n}$ 和 $x \gt \sqrt{n}$ 分类处理，然后保持单次操作复杂度不超过 $O(\sqrt{n})$ 。于是就有了一个很智慧的想法：将数组 $a$ 表示为：

\[a_i = b_i + \sum{c_j (j \leq \sqrt{n} \wedge j|i)} \]

简而言之就是 $j$ 遍历 $i$ 的不超过 $\sqrt{n}$ 的因数。对于 $b$ ， $c$ 两个数组的初始化，容易想到 $c$ 初始全为 $0$ ， $b$ 就是 $a$ 。

操作 $1$ ：如果 $x \leq \sqrt{n}$ ，就给 $c_x$ 加 $k$ ，这就相当于所有以 $x$ 为因数的 $a$ 上加了 $k$ 。否则，暴力给所有 $b_i$ （$i$ 是 $x$ 的倍数）加 $k$ 。

操作 $2$ ：直接暴力给所有 $b_i$ （$i$ 是 $x$ 的因数）加 $k$ 即可。

操作 $4$ ：首先暴力把所有 $b_i$ （$i$ 是 $x$ 的因数）加起来。然后考虑每个 $c_i$ （$1 \leq i \leq \sqrt{n}$）对答案能产生多少次贡献。每当 $x$ 的一个因数 $j$ 让 $c_i$ 产生了一次贡献，就说明 $i$ 是 $j$ 的因数，也就是：

\[x = k_1j = k_1(k_2i) \]

所以 $c_i$ 的贡献次数就是满足上式的 $k_1k_2$ 个数，也就是 $x/i$ 的因数个数。

操作 $3$ ：当 $x \gt \sqrt{n}$ ，首先暴力统计 $b$ 。然后，每当 $x$ 的一个倍数 $j$ 能让 $c_i$ 产生一次贡献，就说明 $j$ 是 $x$ 和 $i$ 的一个公倍数。有多少个这样的 $j$ 呢？ $j$ 是 $LCM(x， i)$ 的倍数，所以个数就是 $n / LCM(x, i)$ 。当 $x \leq \sqrt{n}$ ，如果用类似的方式统计答案，那就一定要暴力统计 $b$ ，这是不可行的。

于是考虑另外维护操作 $3$ 在 $x \leq \sqrt{n}$ 情况下的答案，就是下面代码中的 $sum$ 数组。下面讨论对 $sum$ 的维护。

操作 $1$ ：与上面的操作 $3$ 类似，只有 $i$ 和 $x$ 的公倍数才能对 $sum_i$ 产生贡献，所以 $sum_i$ 要加上 $n / LCM(i, x)$ 个 $k$ 。

操作 $2$ ：如果 $x$ 的一个因数 $j$ 能让 $sum_i$ 加 $k$ ，说明 $j$ 是 $i$ 的倍数，和上面操作 $4$ 的式子完全相同，所以 $sum_i$ 加上 $x/i$ 的因数个数个 $k$ 。

#include <bits/stdc++.h>
// #include <ext/pb_ds/assoc_container.hpp>
// #include <ext/pb_ds/tree_policy.hpp>
// #include <ext/pb_ds/hash_policy.hpp>

using namespace std;
// using namespace __gnu_pbds;

#define int long long
#define ll long long
#define i128 __int128_t
#define float long double
#define ld long double
#define pii array<int, 2>
#define _(x, y) (views::iota((int)x, (int)(y + 1)))
#define __(name, ...) [&](auto const &name) { return __VA_ARGS__; }

using nli = numeric_limits<int>;
using nls = numeric_limits<signed>;
constexpr int INF = 2e16;
constexpr ld eps = 1e-12;

constexpr int N = 5e5 + 5, M = 805;

int n, qnum, m, a[N], c[M], sum[M], g[M][M];
vector<int> fac[N];

inline int mylcm(int x, int y) {
    if (x < y) swap(x, y);
    return x * y / g[y][x % y];
}

inline void solve() {
    cin >> n >> qnum;
    m = (int)sqrt(n);
    for (int i = 1; i <= n; i++) cin >> a[i];
    for (int i = 1; i <= m; i++) {
        for (int j = i; j <= n; j += i) sum[i] += a[j];
    }
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= n / i; j++) fac[i * j].emplace_back(i);
    }
    for (int i = 0; i <= m; i++) {
        for (int j = 0; j <= m; j++) {
            if (!i || !j)
                g[i][j] = i + j;
            else
                g[i][j] = i < j ? g[j % i][i] : g[i % j][j];
        }
    }
    while (qnum--) {
        int op, x, k;
        cin >> op >> x;
        if (op == 1) {
            cin >> k;
            if (x <= m)
                c[x] += k;
            else {
                for (int i = x; i <= n; i += x) a[i] += k;
            }
            for (int i = 1; i <= m; i++) sum[i] += k * (n / mylcm(i, x));
        } else if (op == 2) {
            cin >> k;
            for (int u : fac[x]) a[u] += k;
            for (int i = 1; i <= m; i++) {
                if (x % i == 0) sum[i] += k * fac[x / i].size();
            }
        } else if (op == 3) {
            if (x <= m)
                cout << sum[x] << endl;
            else {
                int ans = 0;
                for (int i = x; i <= n; i += x) ans += a[i];
                for (int i = 1; i <= m; i++) ans += c[i] * (n / mylcm(i, x));
                cout << ans << endl;
            }
        } else {
            int ans = 0;
            for (int u : fac[x]) ans += a[u];
            for (int i = 1; i <= m; i++) {
                if (x % i == 0) ans += c[i] * fac[x / i].size();
            }
            cout << ans << endl;
        }
    }
}

signed main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    int _ = 1;
    // cin >> _;
    while (_--) solve();
    return 0;
}

回到顶部

posted on 2025-07-12 00:45 C12AK 阅读(106) 评论(5) 收藏举报