2025寒假集训补题专辑
ABC155F - Perils in Parallel
题意
有 \(n\) 个炸弹,第i个炸弹位置为 \(pos_i\) ,状态为 \(state_i\) (只能取0或1,分别表示未启动和启动)。有 \(m\) 种可用的操作,第 \(i\) 个操作是将位置在 \(l_i\) 到
\(r_i\) 之间的炸弹的状态全部翻转(未启动变成启动,启动变成未启动)。问是否可以通过一系列可行的操作,使得所有炸弹状态全部变为未启动?如果没有,输出-1;否则先输出用到操作的个数,然后按编号从小到大输出这些操作。
解法
很有意思的一个题。下面的思路是我想到最简单的,并不是赛时用的。
首先考虑将区间修改转化成单点修改:如果先将所有炸弹按位置从小到大排序,然后记
也就是说 \(d_i\) 表示 第i个炸弹的状态和前一个炸弹状态是否相同 ,那么如果要将下标在 \([l, r]\) 内的炸弹状态翻转(用二分查找把题中给的位置区间改成下标区间),由于 \(\forall i \in (l, r]\) , \(state_i\) 和 \(state_{i-1}\) 都要同时变化,那么 \(d_i\) 就不变。只需要翻转 \(d_l\) 和 \(d_{r+1}\) 这两个点就好了。
如何判断所有炸弹都未启动?令 \(state_0 = 0\),它的充要条件是 \(\forall i∈[1, n], d[i] = 0\) 。这个条件就是说, \(state\) 数组开头是0,后面每个位置都和上一个相同。
现在问题就转化成:给出 \(n\) 个0和1,每个操作是翻转其中两个数,问能不能全变成0。
尝试建图解决。 \(n\) 个炸弹作为 \(n\) 个点,每个操作修改的两点间连一条边,同时在边上标记操作编号。每次操作就是翻转一条边的两个端点。这样,得到的图中就形成了若干连通块。由于操作数只有0和1的异或就是模2的加法,而我们的“同时翻转”操作一定从某个值为1的节点 \(u\) 开始,那就可以抽象地想象成把 \(u\) 上的1拿走,移到一个相邻节点 \(v\) 上,然后 \(v\) 处的值模2。进一步地,想象把每个连通块中的1汇聚到同一个点 \(u\) 上,然后将 \(u\) 处值模2,是0就可行,否则直接-1。所以,(我队友说得对,)有解的条件是每个连通块中有偶数个1。
会用到哪些操作(边)呢?在每个连通块上dfs,当走到某节点 \(u\) ,遍历每个未访问的相邻节点 \(v\) ,如果以 \(v\) 为根的dfs子搜索树中有奇数个1,也就是说把这些1全部汇聚到 \(v\) 上,还会剩一个1,就需要把 \(u\) 和 \(v\) 间的边加入答案。最后别忘了把答案中所有边排个序。
超级简单。
Code
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<vector>
#define ll long long
const int N = 2e5 + 5;
int n, m, d[N], bs[N], ans[N], cnt;
bool vis[N];
struct node{
int pos, state;
}a[N];
bool cmp(node n1, node n2){
return n1.pos < n2.pos;
}
struct edge{
int to, id;
edge(int to1 = 0, int id1 = 0){
to = to1, id = id1;
}
};
std::vector<edge> ve[N];
void dfs(int u){
vis[u] = 1;
for(auto v : ve[u]){
if(vis[v.to]) continue;
dfs(v.to);
if(d[v.to]){
d[u]++;
ans[++cnt] = v.id;
}
}
d[u] &= 1;
}
void solve(){
std::cin >> n >> m;
for(int i = 1; i <= n; i++) std::cin >> a[i].pos >> a[i].state;
std::sort(a + 1, a + 1 + n, cmp);
for(int i = 1; i <= n + 1; i++) d[i] = a[i].state ^ a[i - 1].state;
int l, r;
for(int i = 1; i <= n; i++) bs[i] = a[i].pos;
for(int i = 1; i <= m; i++){
std::cin >> l >> r;
l = std::lower_bound(bs + 1, bs + 1 + n, l) - bs;
r = std::upper_bound(bs + 1, bs + 1 + n, r) - bs;
if(l == r) continue;
ve[l].push_back(edge(r, i));
ve[r].push_back(edge(l, i));
}
for(int i = 1; i <= n; i++){
if(vis[i]) continue;
dfs(i);
if(d[i] & 1){
std::cout << "-1\n";
return;
}
}
std::sort(ans + 1, ans + 1 + cnt);
std::cout << cnt << "\n";
for(int i = 1; i <= cnt; i++) std::cout << ans[i] << " ";
std::cout << "\n";
}
signed main(){
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr);
std::cout.tie(nullptr);
int ti = 1;
//std::cin >> ti;
while(ti--) solve();
return 0;
}
ABC154F - Many Many Paths
题意
在二维平面上行走,起点为 \((0, 0)\) ,每一步可以横坐标+1或者纵坐标+1。用 \(f(r, c)\) 表示走到 \((r, c)\) 处的方案数,求
解法
如下图所示, \(f(0, c), f(1, c), ..., f(r, c)\) 都能给 \(f(r, c+1)\) 贡献一个独特的到达方案,所以
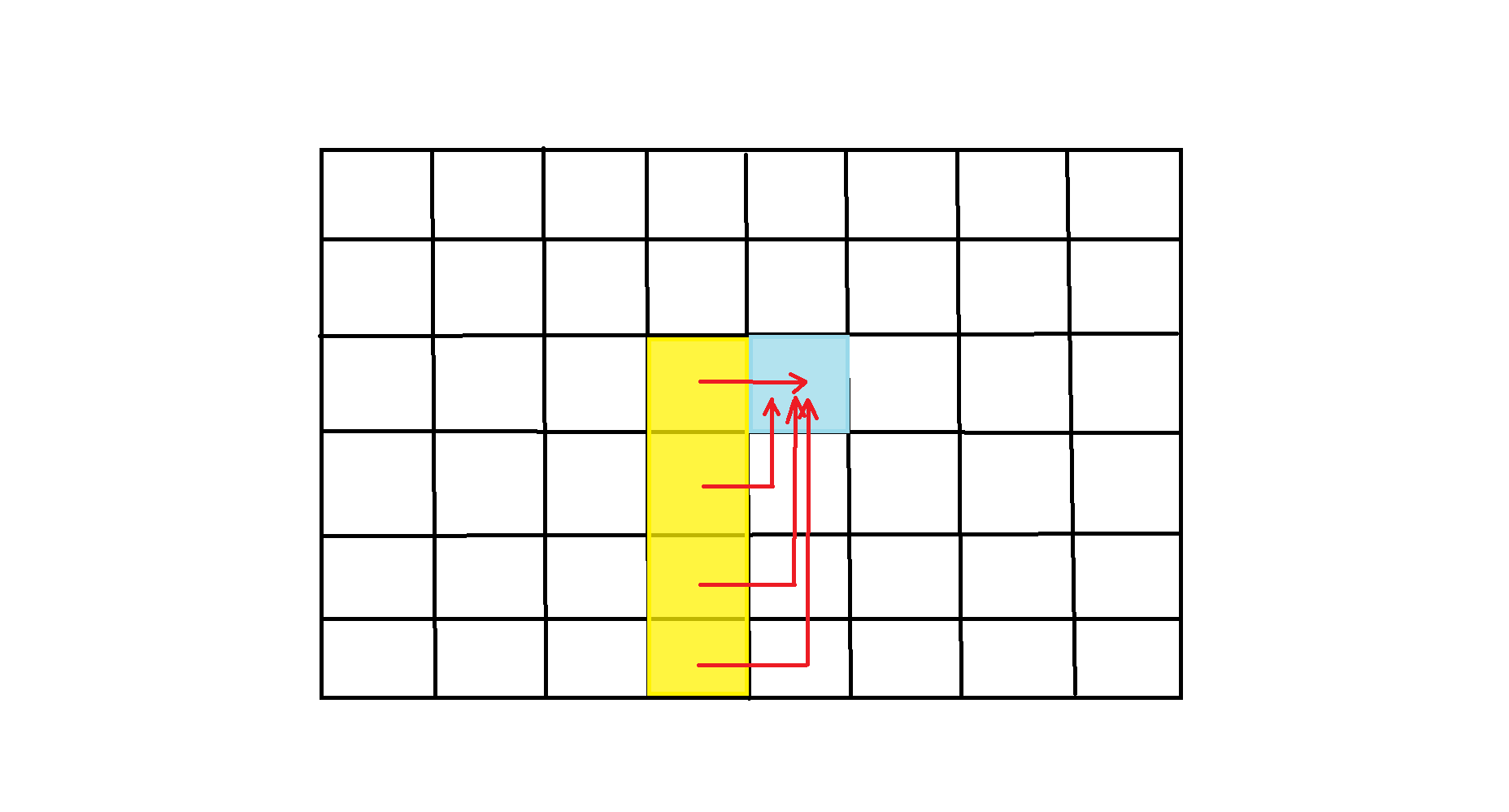
因此,可以将黄色区域的和转换成蓝色区域的和,而蓝色区域加上 \(f(r, 0) = 1\) (绿色)就等于 \(f(r+1, c+1)\) (红色)。
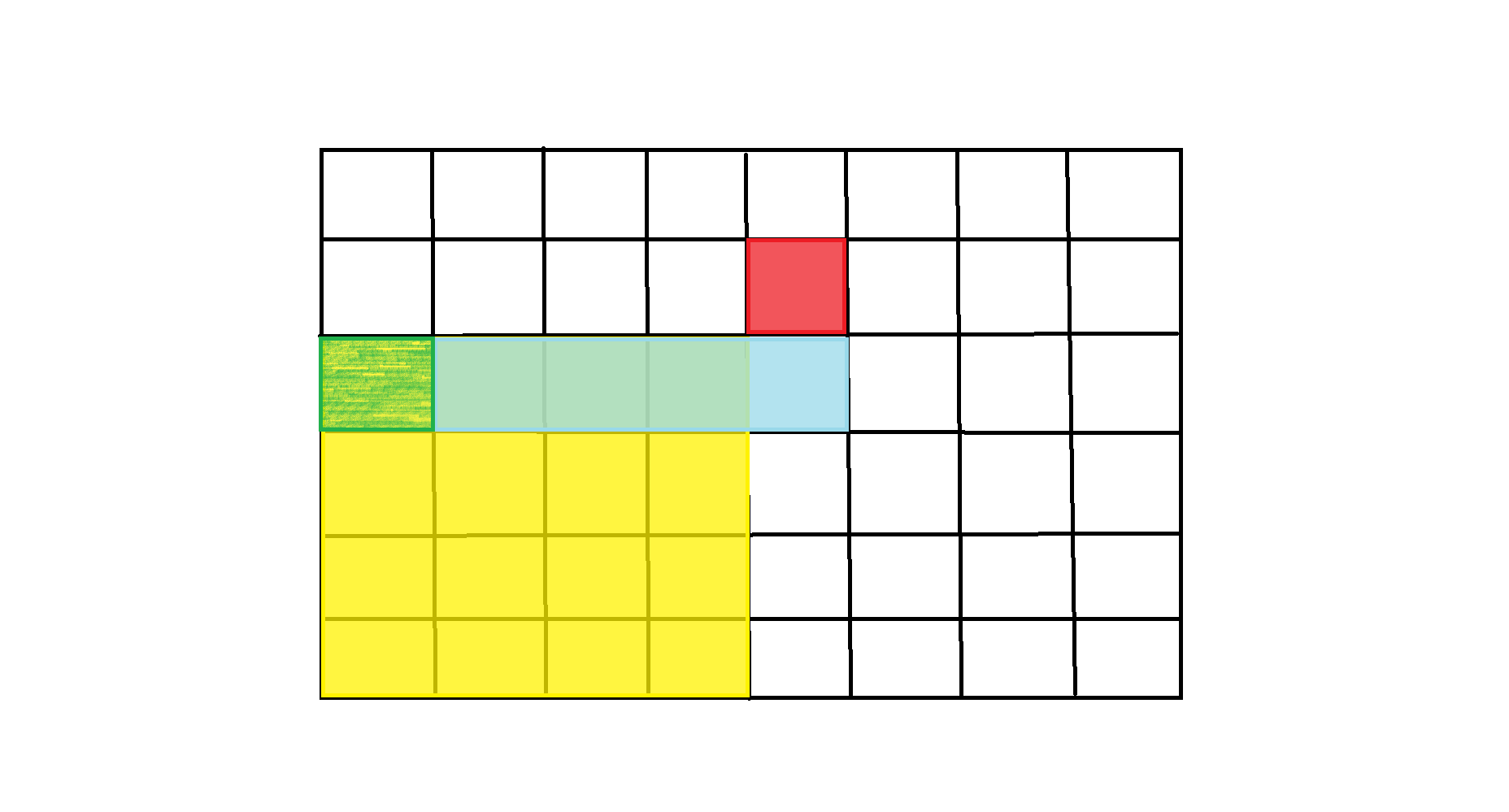
形式化地,
至此,这题就做完了。
Code
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<vector>
#define int long long
const int N = 2e6 + 5;
const int M = 1e9 + 7;
int r1, r2, c1, c2, fac[N];
int fastpow(int a, int b){
int res = 1;
while(b){
if(b & 1) res = res * a % M;
a = a * a % M;
b >>= 1;
}
return res;
}
int comb(int r, int c){
return fac[r + c + 2] * fastpow(fac[r + 1], M - 2) % M * fastpow(fac[c + 1], M - 2) % M;
}
void solve(){
std::cin >> r1 >> c1 >> r2 >> c2;
fac[0] = 1;
for(int i = 1; i <= r2 + c2 + 2; i++) fac[i] = fac[i - 1] * i % M;
std::cout << (comb(r2, c2) - comb(r1 - 1, c2) - comb(r2, c1 - 1) + comb(r1 - 1, c1 - 1) + M * 4) % M << "\n";
}
signed main(){
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr);
std::cout.tie(nullptr);
int ti = 1;
//std::cin >> ti;
while(ti--) solve();
return 0;
}
ABC177F - I hate Shortest Path Problem
题意
在一个 \(h+1\) 行 \(w\) 列的矩阵中行走,可以从第1行的任意列出发,每一步可以往下或者往右走一格(即行+1或者列+1)。但是,在第 \(i\) 行的第 \(l_i\) 到 \(r_i\) 列,不能往下走。对于 \(k \in [2, h+1]\) ,输出到达第 \(k\) 行的最小步数。如果无法到达,输出-1。
解法
考虑从第 \(i\) 行走到第 \(i+1\) 行。用 \(a_{i,j}\) 表示走到 \(i\) 行 \(j\) 列的最小步数。由于我们一行一行处理,可以直接把第一维压缩掉,变成:当前我们已经到达了第 \(i\) 行,要推第 \(i+1\) 行的信息,现在的 \(a_j\) 相当于上述 \(a_{i,j}\) , 而更新后的 \(a_j\) 将会相当于 \(a_{i+1,j}\) 。
为了便于理解,我们不考虑 \(a_{i+1,j}\) 应该如何从上一行推得;我们只考虑 \(a_{i,j}\) 至少应该被用于更新下一行哪些元素,才能保证 一行中的最小值 以及 将会成为最小值的位置 得以保留。首先,如果从当前行的某个位置可以走到下一行,那么它必须参与计算下一行至少一个元素。这是因为,其他位置的值都有可能失效或变大,当前位置即使不在走到下一行的最优路径上,也可能处于到达以后某一行的最优路径上。其次,当前行的一个元素没必要参与计算下一行的多个元素。这是因为,如果这个元素参与计算下一行多个元素,就相当于将 走到当前位置的最优方案 在下一行备份了多次,这是不必要的。
综上:向下更新一行时,对于能向下走的位置,只需把 \(a_{i,j}\) 赋值到 \(a_{i+1,j}\) (直接向下走一步);否则,让 \(a_{i,j} + r_i + 1 - j\) 参与计算 \(a_{i+1,r_i+1}\) (向右走直到能向下)。
具体地,向下更新一行时,令 \(a_{r_i+1} = \min_{j=l_i}^{r_i+1} a_j + (r_i+1-j)\) ,再将 \(a_j, j \in [l_i, r_i]\) 全赋为0,其他位置不变。可以维护两棵线段树:一棵维护 \(a_j\) 区间最小值,用于更新 \(a_j, j \in [l_i, r_i]\) 以及查询答案;另一棵维护 \(a_j-j\) 区间最小值,用于更新 \(a_{r_i+1}\) 。
Code
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#define int long long
const int N = 2e5 + 5;
int h, w;
int a[N * 4], d[N * 4], atag[N * 4], dtag[N * 4];
void build_d(int l, int r, int p){
if(l == r){
d[p] = -l;
return;
}
int mid = l + ((r - l) >> 1);
build_d(l, mid, p << 1);
build_d(mid + 1, r, p << 1 | 1);
d[p] = std::min(d[p << 1], d[p << 1 | 1]);
}
void pushdown(int l, int r, int p){
if(atag[p]){
a[p << 1] = atag[p << 1] = a[p << 1 | 1] = atag[p << 1 | 1] = atag[p];
atag[p] = 0;
}
if(dtag[p]){
d[p << 1] = dtag[p << 1] = d[p << 1 | 1] = dtag[p << 1 | 1] = dtag[p];
dtag[p] = 0;
}
}
void update(int l, int r, int p, int s, int t, int x){
if(s <= l && r <= t){
a[p] = atag[p] = x;
d[p] = dtag[p] = x - t;
return;
}
pushdown(l, r, p);
int mid = l + ((r - l) >> 1);
if(s <= mid) update(l, mid, p << 1, s, t, x);
if(t > mid) update(mid + 1, r, p << 1 | 1, s, t, x);
a[p] = std::min(a[p << 1], a[p << 1 | 1]);
d[p] = std::min(d[p << 1], d[p << 1 | 1]);
}
int query_d(int l, int r, int p, int s, int t){
if(s <= l && r <= t) return d[p];
pushdown(l, r, p);
int mid = l + ((r - l) >> 1), res = (int)2e12;
if(s <= mid) res = std::min(res, query_d(l, mid, p << 1, s, t));
if(t > mid) res = std::min(res, query_d(mid + 1, r, p << 1 | 1, s, t));
return res;
}
void solve(){
std::cin >> h >> w;
int l, r;
build_d(1, w, 1);
for(int i = 1; i <= h; i++){
std::cin >> l >> r;
if(r < w){
int minn = query_d(1, w, 1, l, r + 1);
update(1, w, 1, r + 1, r + 1, minn + r + 1);
}
update(1, w, 1, l, r, (int)2e16);
if(a[1] > (int)1e9) std::cout << "-1\n";
else std::cout << a[1] + i << "\n";
}
}
signed main(){
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr);
std::cout.tie(nullptr);
int ti = 1;
//std::cin >> ti;
while(ti--) solve();
return 0;
}
CF1534E - Lost Array
题意
交互题。有一个长为 \(n\) 的未知数组 \(a\) ,你每次可以对交互机输出 \(k\) 个下标 \(b_1, b_2, ..., b_k\) ,评测机会返回 \(a_{b_1} \oplus a_{b_2} \oplus ... \oplus a_{b_k}\) 的值。要求用最少的询问次数,输出 \(a\) 中所有元素的异或和。
解法
思考这道题时,比较自然的想法是先想如何使询问次数最少,再模拟实现这个方案。由于 具体哪些元素的异或和已知 是无关紧要的,我们只需要知道 已知多少个元素的异或和 ,类似“翻硬币问题”。于是,可以用 \(d_i\) 表示 得到其中 \(i\) 个元素的异或和所需的最少询问次数 ,那当改变 \(k\) 个元素的已知性,就可以将 \(i\) 个未知元素改为已知,同时将 \(k-i\) 个已知元素改为未知。
这里,由于一次询问中的元素两两不同,所以要求目前至少有 \(i\) 个未知元素、 \(k-i\) 个已知元素。可得 \(i\) 的取值范围。
满足上述条件时, \(d_{u+k-2i} = d_u + 1\) 。据此跑bfs, \(d_n\) 就是最少操作数。bfs时记下每个状态的前一个状态,然后从 \(n\) 个元素全部已知的状态开始回溯整个过程,按前述方法选取元素询问即可。
Code
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>
#define ll long long
const int N = 505;
int n, k, d[N], pre[N], ans[N];
std::queue<int> q, known, unknown;
int ask(int x){
std::cout << "?";
for(int i = 0; i < x; i++){
std::cout << " " << unknown.front();
known.push(unknown.front());
unknown.pop();
}
for(int i = 0; i < k - x; i++){
std::cout << " " << known.front();
unknown.push(known.front());
known.pop();
}
std::cout << std::endl;
int rep;
std::cin >> rep;
return rep;
}
void solve(){
std::cin >> n >> k;
for(int i = 1; i <= n; i++) d[i] = -1;
q.push(0);
while(!q.empty()){
int u = q.front();
q.pop();
for(int i = std::max(0, k + u - n); i <= std::min(k, u); i++){
int v = u + k - i * 2;
if(d[v] == -1){
d[v] = d[u] + 1;
pre[v] = u;
q.push(v);
}
}
}
if(d[n] == -1){
std::cout << "-1\n";
return;
}
ans[d[n]] = n;
for(int i = d[n] - 1; i > 0; i--) ans[i] = pre[ans[i + 1]];
for(int i = 1; i <= n; i++) unknown.push(i);
int res = 0;
for(int i = 1; i <= d[n]; i++) res ^= ask((ans[i] - ans[i - 1] + k) / 2);
std::cout << "! " << res << std::endl;
}
signed main(){
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr);
std::cout.tie(nullptr);
int ti = 1;
//std::cin >> ti;
while(ti--) solve();
return 0;
}
ABC288E - Wish List
题意
有 \(n\) 个商品,编号从1到 \(n\) ,编号为 \(i\) 的商品价格是 \(a_i\) ,每个编号的商品只有一个;此外,又给出一个长为 \(n\) 的数组 \(c\) 。现在需要买 \(m\) 个商品,编号分别是 \(x_1, x_2, ..., x_m\) 。当购买编号为 \(i\) 的商品时,如果它是 还没被购买的商品中 的第 \(j\) 个,那么花费就是 \(a_i+c_j\) 。请问买到需要的所有商品的最小花费(可以买不需要的商品)。
解法
当购买第 \(i\) 个商品,后续所有商品对应的 \(c\) 都会前移一个位置。如果买第 \(i\) 个商品之前买了 \(j\) 个 在它前面的 商品,那 \(a_i\) 就对应 \(c_{i-j}\) 。如果最终买了第 \(i\) 个商品前面的 \(j\) 个商品,那么在整个过程中, \(a_i\) 有可能对应 \(c_j, j \in [i-j, i]\) ;当然,我们取 \(\min_{k=i-j}^i c_k\) 。
设 \(dp_{i,j}\) 表示前 \(i\) 个物品中买了 \(j\) 个的最小花费。考虑第 \(i\) 个商品。如果购买,那么
如果不购买,那么
如果必须买,就只用第一个式子,否则二者取最小值。
Code
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#define int long long
const int N = 5005;
int n, m, a[N], c[N], minn[N][N], dp[N][N];
bool f[N];
void solve(){
std::cin >> n >> m;
for(int i = 1; i <= n; i++) std::cin >> a[i];
for(int i = 1; i <= n; i++) std::cin >> c[i];
int x;
for(int i = 1; i <= m; i++){
std::cin >> x;
f[x] = 1;
}
for(int i = 1; i <= n; i++){
minn[i][i] = c[i];
for(int j = i + 1; j <= n; j++){
minn[i][j] = std::min(minn[i][j - 1], c[j]);
}
}
for(int i = 0; i <= n; i++){
for(int j = 0; j <= n; j++) dp[i][j] = (int)1e16; // 下文提到的位置
}
dp[0][0] = 0;
for(int i = 1; i <= n; i++){
if(!f[i]){
for(int j = 0; j <= i; j++){
dp[i][j] = std::min(dp[i][j], dp[i - 1][j]);
}
}
for(int j = 1; j <= i; j++){
dp[i][j] = std::min(dp[i][j], dp[i - 1][j - 1] + minn[i - (j - 1)][i] + a[i]);
}
}
int ans = dp[n][m];
for(int i = m + 1; i <= n; i++) ans = std::min(ans, dp[n][i]);
std::cout << ans << "\n";
}
signed main(){
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr);
std::cout.tie(nullptr);
int ti = 1;
//std::cin >> ti;
while(ti--) solve();
return 0;
}
注意:代码中带注释那一行, \(j\) 的初值不能是1。因为,如果直到第 \(i\) 个商品都不是必选,那么 \(dp_{i,0}\) 应该为0(令初值 \(j=0\) 则可以从 \(dp_{0,0}\) 一路转移过来);如果前 \(i\) 个商品有必选的,那么 \(dp_{i,0}\) 应该是不可达的,设为无穷大。
回到顶部



 浙公网安备 33010602011771号
浙公网安备 33010602011771号