「网络流」学习笔记
给出一个有向图,有源点\(S\)和汇点\(T\)。每条边有一个容量,现在要从源点开始流,每条边不能超过其容量。在流的过程中有许多问题,最大流、费用流等等。许多问题都可以通过网络流来建模。
最大流
最大流问题就是问从源点出发流到汇点,汇点最多能流到多少。
概念
反向边
如果直接流,有时不会是最优的。
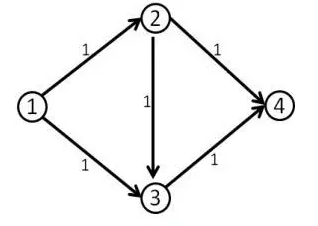
此时我们考虑加入反向边。考虑从\(u\)流到\(v\)的流量为\(f\),那么等价于从\(v\)流到\(u\)的流量为\(-f\)。
增广路
加入反向边之后每找到一条可流的路就去流,直到无法再增加。称这样一条可行的路为增广路。只要不断寻找增广路即可求出最大流。
残量网络
定义:残量=容量-流量
这样增广路就对应残量网络中一条边权全部为正的路径。增广路增广的值就是这条路径中残量的最小值。
设一条边容量为\(c\),流量为\(f\)。则其残量为\(c-f\)。
这条边的反向边流量为\(-f\),其残量应为\(f\),故反向边的容量应为\(0\)。
增广路定理
当且仅当残量网络中不存在一条从\(S\)到\(T\)的增广路时,此时的流是最大流。
EK算法
\(BFS\)每次只寻找一条增广路,找到以后增广,然后重复之前步骤直到找不到增广路结束。
inline void EK(){
int u;
for(;;){
memset(a,0,sizeof(a));
while(!q.empty()) q.pop();
q.push(S);
a[S] = INF;
while(!q.empty()){
u = q.front(); q.pop();
for(int i = head[u]; i != -1; i = nxt[i]){
if(!a[to[i]] && c[i]-f[i]>0){
pre[to[i]] = i;//这一步我们记录边的编号,以便更新流量。我们只需要在一次BFS中找一条增广路,而每一次发现一条边可行便更新其对应终点对应的边,因为u已经可行所以这样记录一定没有问题。结束后从T点向前找一定能找到对应增广路
a[to[i]] = min(a[u],c[i]-f[i]);
q.push(to[i]);
}
}
if(a[T]) break;
}
if(!a[T]) break;
for(int x = T; x != S; x = from[pre[x]]){
f[pre[x]] += a[T];
f[pre[x]^1] -= a[T];
}
ans += a[T];
}
}
Dinic算法
每一轮只考虑残量>0的边,进行\(BFS\)分层,每一次规定增广路的边必须连接相邻两个层。这样做的意义是每次只找确定长度的增广路对流量的贡献,这样最多进行\(n\)次分层即可完成整个最大流的求解。
分层之后\(DFS\)找增广路。这里进行多路增广,也就是一次DFS找出多条增广路一起增广。
每一次在\(DFS\)的过程中传入参数\(a\)表示当前点出发的最大流量,在回溯时判断从这一步走能否找到增广路,并返回找到的增广路的贡献更新。
当前弧优化
在分层图确定的情况下,每个点只\(DFS\)一次。因此一个点出发的每一条边都不需要重复搜索。由于边的顺序是确定的,用一个数组记录前多少条边已经搜过了,避免重复搜索。
\(Code\)
/*DennyQi 2019*/
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <queue>
using namespace std;
const int N = 10010;
const int M = 100010;
const int P = 998244353;
const int INF = 0x3f3f3f3f;
inline int read(){
int x(0),w(1); char c = getchar();
while(c^'-' && (c<'0' || c>'9')) c = getchar();
if(c=='-') w = -1, c = getchar();
while(c>='0' && c<='9') x = (x<<3)+(x<<1)+c-'0', c = getchar();
return x*w;
}
int n,m,S,T,ans,x,y,z,cur[N],h,t,q[N],lv[N];
int head[N],nxt[M<<1],to[M<<1],c[M<<1],f[M<<1],cnte=-1;
inline int corres(int i){
return (i&1) ? i+1 : i-1;
}
inline void add(int u, int v, int C, int F){
to[++cnte] = v;
c[cnte] = C;
f[cnte] = F;
nxt[cnte] = head[u];
head[u] = cnte;
}
inline bool BFS(){
memset(lv,0,sizeof(lv));
h = t = 0;
int u;
lv[S] = 1;
q[++t] = S;
while(h < t){
u = q[++h];
for(int i = head[u]; i != -1; i = nxt[i]){
if(lv[to[i]] || c[i]-f[i]==0) continue;
lv[to[i]] = lv[u]+1;
q[++t] = to[i];
}
}
return lv[T];
}
//DFS(u,a)返回在当前状态下,从$u$出发,该点初始容量为$a$的最大可行流。
int DFS(int u, int a){
if(u == T || !a) return a;
int res=0, F;
for(int& i = cur[u]; i != -1; i = nxt[i]){
if(lv[to[i]]==lv[u]+1 && c[i]-f[i]>0){
F = DFS(to[i],min(a,c[i]-f[i]));
a -= F;
res += F;
f[i] += F, f[i^1] -= F;
if(!a) break;
}
}
return res;
}
inline void Dinic(){
while(BFS()){
for(int i = 1; i <= n; ++i) cur[i] = head[i];
ans += DFS(S,INF);
}
}
int main(){
// freopen("file.in","r",stdin);
n = read(), m = read(), S = read(), T = read();
memset(head,-1,sizeof(head));
for(int i = 1; i <= m; ++i){
x = read(), y = read(), z = read();
add(x,y,z,0);
add(y,x,0,0);
}
Dinic();
printf("%d\n",ans);
return 0;
}
最小割
给出一张有源点和汇点的图,删去若干边使得源点与汇点不连通,删去的边的权值和成为割。
最小割=最大流
最小费用最大流
给每条边附上一个权值\(v\)。流过一条边的代价是\(v*f\),即\(v\)代表单位流量的费用。最大流是确定的,流法有很多种。现在要求出最小费用的最大流。
算法是使用\(EK\)。普通的\(EK\)是用\(BFS\)来求增广路的,现在就用\(v\)作为边权做最短路。这样保证每一次增广都使增加的费用最少,因此全部增广后费用也一定最少。
/*DennyQi 2019*/
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <queue>
using namespace std;
const int N = 5010;
const int M = 50010;
const int P = 998244353;
const int INF = 0x3f3f3f3f;
inline int read(){
int x(0),w(1); char c = getchar();
while(c^'-' && (c<'0' || c>'9')) c = getchar();
if(c=='-') w = -1, c = getchar();
while(c>='0' && c<='9') x = (x<<3)+(x<<1)+c-'0', c = getchar();
return x*w;
}
int n,m,S,T,x,y,z,p,ans1,ans2,pre[N],inq[N],d[N];
int head[N],nxt[M<<1],to[M<<1],from[M<<1],c[M<<1],f[M<<1],val[M<<1],cnte=-1;
queue <int> q;
inline void add(int u, int v, int C, int F, int V){
to[++cnte] = v, from[cnte] = u;
c[cnte] = C, f[cnte] = F, val[cnte] = V;
nxt[cnte] = head[u];
head[u] = cnte;
}
inline bool spfa(){
memset(d,0x3f,sizeof(d));
memset(inq,0,sizeof(inq));
memset(pre,-1,sizeof(pre));
q.push(S);
d[S] = 0;
while(!q.empty()){
int u = q.front(); q.pop();
inq[u] = 0;
for(int i = head[u]; i != -1; i = nxt[i]){
if(c[i]-f[i] > 0 && d[u]+val[i] < d[to[i]]){
d[to[i]] = d[u]+val[i];
pre[to[i]] = i;
if(!inq[to[i]]){
inq[to[i]] = 1;
q.push(to[i]);
}
}
}
}
return pre[T]!=-1;
}
inline void EK(){
while(spfa()){
int a = INF;
for(int x = T; x != S; x = from[pre[x]]){
a = min(a,c[pre[x]]-f[pre[x]]);
}
ans1 += a;
for(int x = T; x != S; x = from[pre[x]]){
f[pre[x]] += a;
f[pre[x]^1] -= a;
ans2 += a*val[pre[x]];
}
}
}
int main(){
// freopen("file.in","r",stdin);
memset(head,-1,sizeof(head));
n = read(), m = read(), S = read(), T = read();
for(int i = 1; i <= m; ++i){
x = read(), y = read(), z = read(), p = read();
add(x,y,z,0,p);
add(y,x,0,0,-p);
}
EK();
printf("%d %d\n",ans1,ans2);
return 0;
}
最大权闭合子图
闭合子图是指在有向图中选择一个点集,每个点被选择之后必须选择其后代节点。最大权闭合子图就是要使闭合子图的点权之和最大。
在具体问题中,原图一般类似二分图,分为\(A\),\(B\)两部。类似二分图建立网络流,其中AB之间的边容量为\(\infty\),其余边为点权的绝对值。
最大权闭合子图=正权和-最小割。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号